目录
一、背景
1、集群
2、集群智能
3、集群应用
4、协调控制
(1)一致性控制
(2)编队控制
二、多机器人集群运动的协同控制
1、运动到指定点
2、三星模型
3、日地月模型
4、三角形模型
三、二轮差动小车数学模型
1、理论分析
2、构建simulink模型
四、多二轮差动小车协同控制
1、运动到指定点
2、三星模型
3、日地月模型
4、三角形模型
五、相关资料
一、背景
1、集群
集群是生物中常见的一种生存现象,如昆虫、鸟类、鱼类、动物、微生物乃至我们人类等。如下图所示,鸟或鱼形成一个巨大的群的壮观景象,这在自然界并非少见。生物的这些特性是在漫长的进化过程中逐渐形成的,对他们的生存和进化有着十分重要的影响,同时这些方式为人类解决问题的思路带来了不少启发和鼓舞。近年来,有不少科学家对生物集群的行为进行了广泛的研究,并逐渐形成了一种基于生物集群行为的解决方式。


图1、大自然中的集群现象
2、集群智能
生物界中,群居生物中的每一个个体看上去都有自身的行动方式,并且整个群体在整体上呈现出高度的有组织性。显然,所有个体活动的完美集成过程中不需要任何的指导。事实,研究社会性昆虫的科学家发现在群体中的协作是高度自组织的,它们的协调行为是通过个体之间的交互行为直接实现,或者个体与环境的交互行为间接实现的。虽然这些交互行为非常简单,但是他们聚在一起却能解决一些难题。这种潜在方式被称为集群智能,已经逐渐为人们所认识并得到应用。
3、集群应用
通常情况下,一个集群被定义为一群自治体的集合,他们通过相互间直接的或者间接的通讯,从而通过全体的活动来解决一些分布式的难题。在这里,指在一个环境中具备自身活动能力的一个实体,其自身力求简单,通常不必具有高级智能。
Reynolds按照自然界中鸟群的特点,对鱼群、鸟群等系统的群体行为进行了计算机模拟,提出了著名的Boid模型。每只虚拟的鸟都作为一个独立的因素,它们通过感知周围局部的动态环境来确定自身飞行的路线,在仿真过程中每只虚拟的鸟主要采用了三个行为:
(1)防止碰撞:避免与周围的同伴发生碰撞;
(2)速度匹配:试图使自身的速度与周围伙伴的速度一致;
(3)中心聚拢:试图向附近的同伴聚拢。
研究表明,一定数量的这种虚拟鸟能够在复杂的环境中聚集成群并自由避开障碍物。
4、协调控制
针对群体行为,多个体之间的协调与合作将大大提高个体行为的智能化程度,更好地完成很多单个个体无法完成的工作,并具有高效率,高容错性和内在的并行性等优点。而多个体协调控制的基本问题包括多个体协调控制的基本问题包括一致性控制、会合控制、聚结控制和编队控制,其中后三者可视为一致性控制的推广与特例。下面对一致性控制和编队控制将进行简述。
(1)一致性控制
一致性是指多个体通过信息的共享与交互,实现某种状态的趋同,其控制目标可描述为
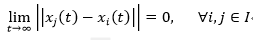
其中,I为系统中个体的集合,x_i为系统中第i个个体的状态。
1)对于一阶积分器型线性系统,其动力学模型为
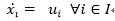
其中,x_i∈R为第i个个体的状态,u_i为施加的控制量。
对应的协调控制律可设计为:
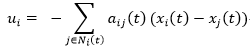
其中,j∈N_i (t)表示第i个个体的相邻个体集合,a_ij (t)为时变的拓扑加权系数。上述控制律意味着每个个体的状态不断趋同于其相邻个体的状态。
2)对于二阶积分器型线性系统,其动力学模型为
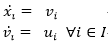
对应的一致性控制律可设计为:
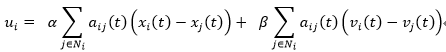
以经典控制的视角来看 , 该控制器本质上是一个PD控制器,即协调控制律中既包含位置误差信息,也包含速度误差信息。所不同的是,对于多个体系统而言,其利用的是群体性误差信息,而针对单体系统的控制仅需要该单体与期望状态的误差信息。
(2)编队控制
编队控制是多个体协调控制中的一个研究热点,其本质是一种几何构型严格的聚结控制。编队控制的目标在于通过调整个体的行为使系统实现特定几何构型的整体性位移,其数学描述为
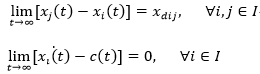
其中,x_dij为第i个与第j个个体的期望相对位置矢量,c(t)为期望的整体位移速度。
目前,编队控制大致可分为三类,即主从式、虚拟结构式和行为式。
1)主从式
主从式方法中,多个体系统中的一个或几个个体充当“主体”,其他个体充当“从体”并通过与其相邻个体的交互达到跟随主体的目的。
2)虚拟结构式
虚拟结构是一种广为采用的编队控制方法。该构架下,通过对所有个体状态进行一定的代数运算生成一个虚拟个体,整个编队被视为一个刚体,而虚拟的个体就成为参考点。
3)行为式
行为式方法中针对每个个体预定义一个合适的控制律,使其对应于所有个体可能的状态
二、多机器人集群运动的协同控制
将机器人看作是质点,以二阶积分器模型为研究对象,观察多机器人集群运动的协同控制,其中,三个机器人之间的通讯可用下图表示
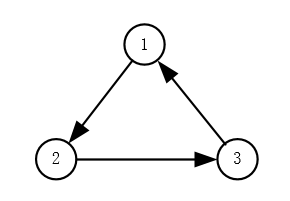
图2、机器人之间的通讯关系
1、运动到指定点
三个机器人的初始位置为(0,2)、(10,2)、(5,10),使其运动到指定的点(3,3)、(4,4)、(5,5)。其simulink模型如图3所示,结果如图4所示
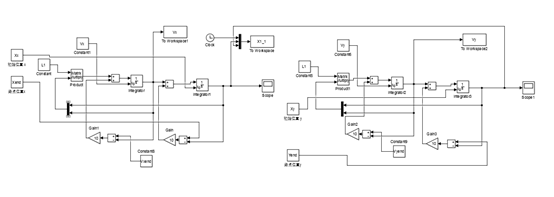
图3、运动到指定点的simulink模型
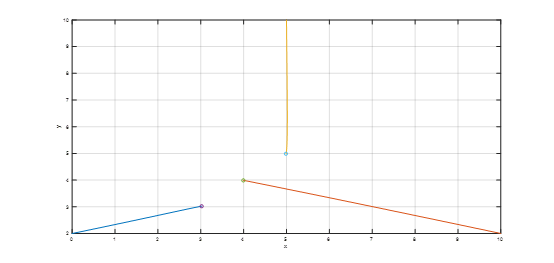
图4、运动到指定点的仿真结果
2、三星模型
三个机器人从初始位置(0,2)、(10,2)、(5,10)运动到指定至圆心为(10,10),半径为2的圆上,绕着圆旋转并使他们之间相隔120度,构建出三星模型。其simulink模型如图5所示,结果如图6所示
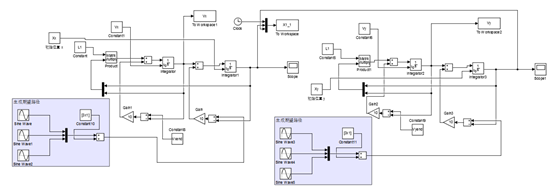
图5、三星模型的simulink模型
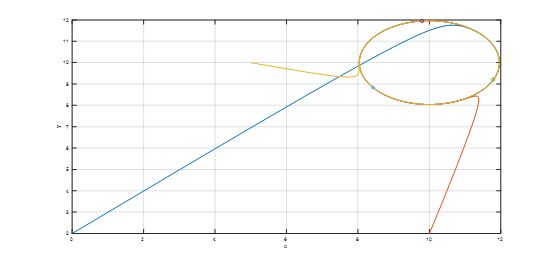
图6、三星模型的仿真结果
3、日地月模型
三个机器人从初始位置(0,2)、(10,2)、(5,10)运动到指定路径,第一个机器人运动到指定点(5,5),第二个机器人运动在以(5,5)为圆心,半径为2的圆上,第三个机器人指运动到以第二个机器人位置为圆心,半径为0.5的圆上,从而构建出日地月模型。其simulink模型如图7所示,结果如图8所示
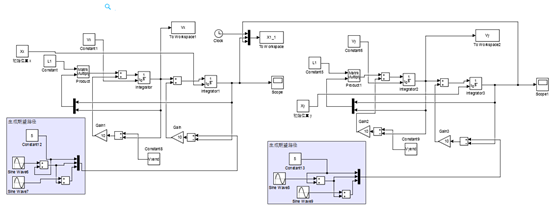
图7、日地月模型的simulnk模型
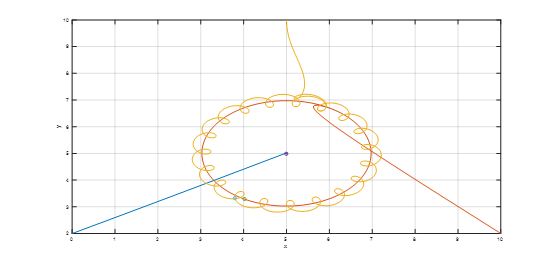
图8、日地月模型的仿真结果
4、三角形模型
三个机器人从初始位置(0,2)、(10,2)、(5,10)运动到指定路径,即以(5,5)、(10,0)、(5+5cos(pi/3),5sin(pi/3))构成的三角形,其simulink模型如9所示,结果如图10所示
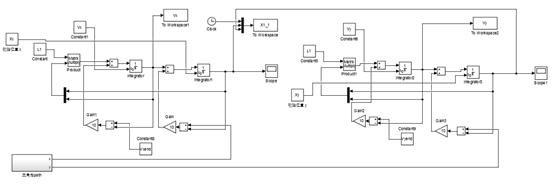
图9、三角形模型的simulink模型
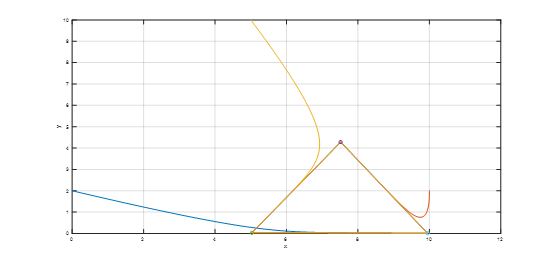
图10、三角形模型的仿真结果
三、二轮差动小车数学模型
1、理论分析
针对二轮差动小车模型,如图11所示,其中,vl、vr分别指小车左轮和右轮的速度,L指小车的宽度,R指小车车轮的半径
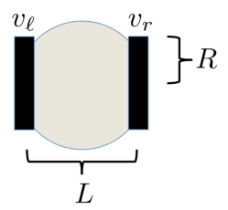
图11、二轮差动小车模型
即,小车移动速度的x分量及y分量、小车的角速度与左右轮移动速度、转向角度之间的关系可描述为
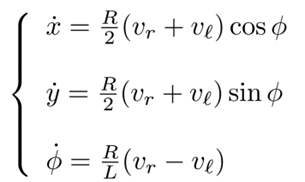
其中,(x,y)为小车位置,Ф为小车的转向角度
若将小车看作质点,如图12所示,其中,(x,y)为小车位置,Ф为小车的转向角度
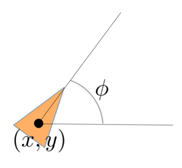
图12、质点小车模型
由上图我们可以轻易地得出,
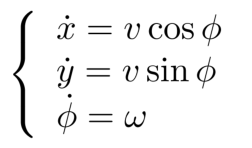
其中,v和w分别指小车的运动速度和角速度
由以上公式,我们可以推出,
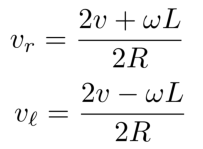
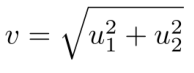
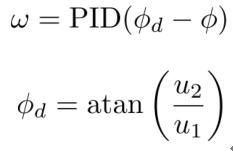
其中,u1和u2分别指小车速度的x分量和y分量
2、构建simulink模型
根据上述的理论推导,小车的simulink模型为
(1)左右轮速度的求解
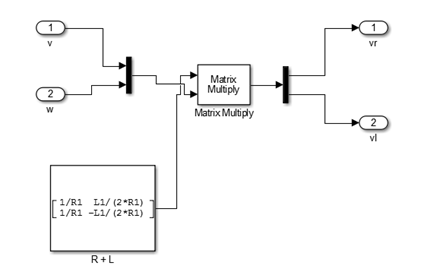
(2)小车位置及转向角度的求解
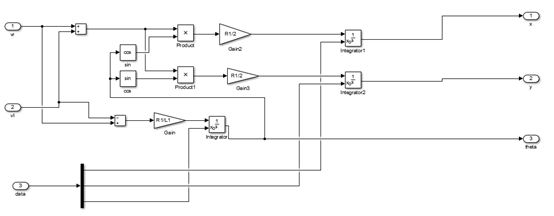
(3)速度与转向角度求解
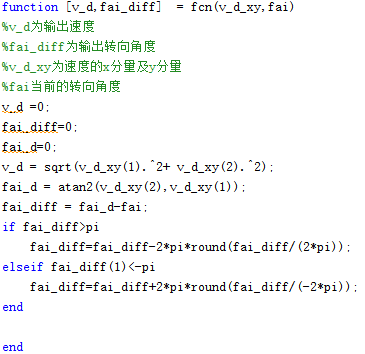
(4)角速度的求解
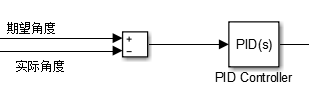
(5)整体simulink模型
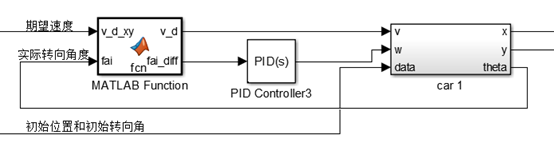
四、多二轮差动小车协同控制
结合上述的多机器人集群运动协调控制模型及二轮差动小车模型,研究多二轮差动小车的协调控制。其主要思想是,将机器人看作质点,得出各个机器人的速度信息,从而计算出期望速度和期望角速度。再将它们传给二轮差动小车模型,通过PID调节,使二轮差速小车模型跟随期望值,从而实现多二轮小车的协同控制。
多二轮差动小车协同控制的整体simulink模型如图13所示,重要部分simulink模型如图14、图15、图16所示
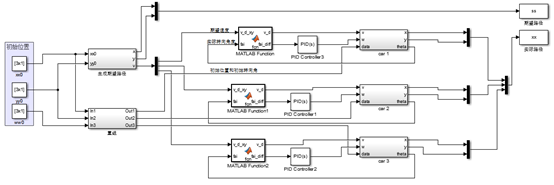
图13、整体simulink模型
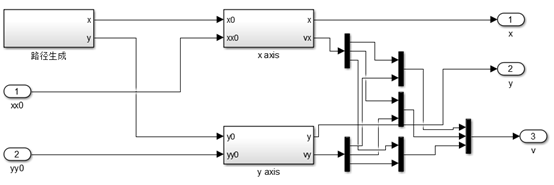
图14、生成期望路径模块simulink模型
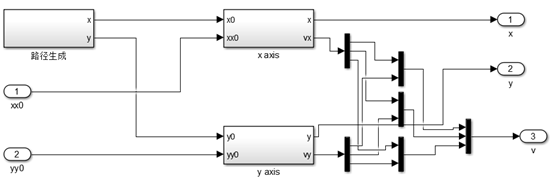
图15、生成期望路径模块中x axis模块simulink模型
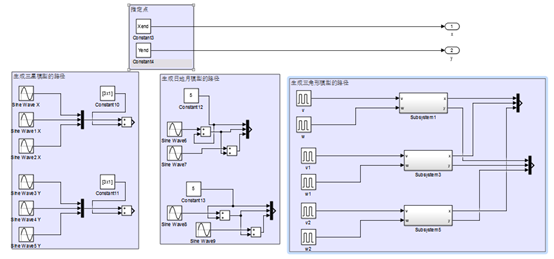
图16、生成期望路径模块中路径生成模块simulink模型
1、运动到指定点
三个机器人从初始位置为(0,2)、(10,2)、(5,10)出发,使其运动到指定的点(3,3)、(4,4)、(5,5)。多二轮差动小车协同控制仿真结果如图17所示
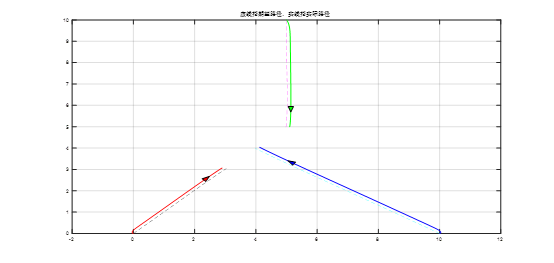
图17、运动到指定点仿真结果
2、三星模型
三个机器人从初始位置(0,2)、(10,2)、(5,10)出发,使其构成三星模型。多二轮差动小车协同控制仿真结果如图18所示
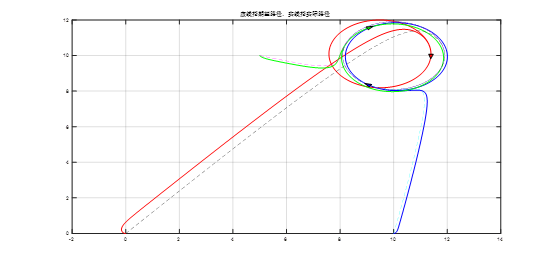
图18、三星模型仿真结果
3、日地月模型
三个机器人从初始位置(0,2)、(10,2)、(5,10)出发,使其构成日地月模型。多二轮差动小车协同控制仿真结果如图19所示
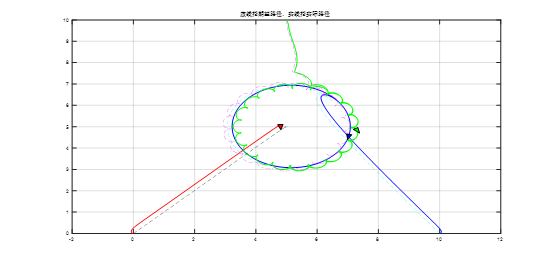
图19、日地月仿真模型
4、三角形模型
三个机器人从初始位置(0,2)、(10,2)、(5,10)出发,使其构成三角形模型。多二轮差动小车协同控制仿真结果如图20所示
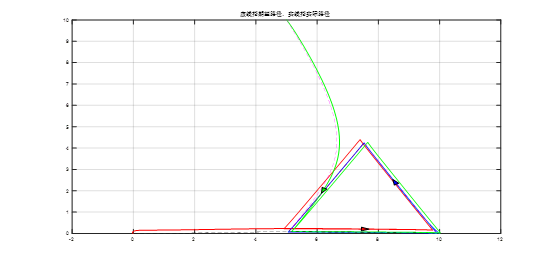
图20、三角形模型仿真结果
五、 相关资料
参考文献及相关simulink模型可从下面的百度网盘提取或者github网站
链接: https://pan.baidu.com/s/18uNAuHwC6PwYd_9-w4hoLw
提取码: cfwc
github:https://github.com/yushen007/----simulink
(附:若有疑问或错误,可联系本人邮箱13682749369@163.com)
最后
以上就是故意黑夜最近收集整理的关于集群机器人规划与控制--基于simulink一、背景二、多机器人集群运动的协同控制三、二轮差动小车数学模型四、多二轮差动小车协同控制五、 相关资料的全部内容,更多相关集群机器人规划与控制--基于simulink一、背景二、多机器人集群运动的协同控制三、二轮差动小车数学模型四、多二轮差动小车协同控制五、内容请搜索靠谱客的其他文章。








发表评论 取消回复