Matlab-具有最优传力性能的曲柄滑块机构的设计程序讲解
序言
大家好,许久不见,最近一直再忙课程设计………没时间更新……望海涵看到标题工科生应该很快就能明白今天blog的核心内容,其实不是工科的也没事,互联网时代,专业早已不是限制门槛,所有学科几乎相互贯通,互联网时代获取信息可谓是简单至极,就像大家百忙之中抽取时间读一下鄙人的陋文,不也拙实令不才欣喜万分
曲柄滑块机构介绍
曲柄滑块机构是指用曲柄和滑块来实现转动和移动相互转换的平面连杆机构。曲柄滑块机构中与机架构成移动副的构件为滑块,通过转动副联接曲柄和滑块的构件为连杆。
曲柄滑块机构广泛应用于往复活塞式发动机、压缩机、冲床等的主机构中,把往复移动转换为不整周或整周的回转运动;压缩机、冲床以曲柄为主动件,把整周转动转换为往复移动。偏置曲柄滑块机构的滑块具有急回特性,锯床就是利用这一特性来达到锯条的慢进和空程急回的目的。
曲柄滑块机构的分类
对心曲柄滑块机构
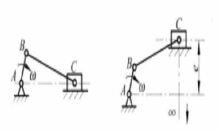
下图1左所示的曲柄滑块机构,滑块的导路中心线通过曲柄的回转中心A,为对心曲柄滑块机构。如果将对心曲柄滑块机构中的滑块C作为机构运动的输出件,则滑块C运动到两个极限位置时,原动件曲柄AB在对应位置间的夹角等于零,即机构的极位夹角为0°,说明对心曲柄滑块机构没有急回运动特性。
偏置曲柄滑块机构
下图1右所示曲柄滑块机构,滑块的导路中心线不通过曲柄的回转中心A,为偏置曲柄滑块机构。与对心曲柄滑块机构不同,如果将偏置曲柄滑块机构中的滑块C作为机构运动的输出件,则偏置曲柄滑块机构具有急回运动特性。
曲柄滑块机构设计常见问题
机器种类很多,但它们都是由各种机构组成的,曲柄滑块机构就是常用机构之一。它有一个重要特点是具有急回特性。故按行程速比系数K设计具有最优传力性能的曲柄滑块机构是设计中常遇到的问题。本文将x作为设计变量,给出了解决问题的方法。
可以公开的情报(所用公式参考网上已公开论文)
(公式参考:具有最优传力性能的曲柄滑块机构的设计——宁海霞 董萍,文末附录原文档)
(本文不在于讲解原理与推导公式,只选择原理文档重要之处摘录,不懂之处滑到文末查看原文档,重点在于matlab仿真分析)
---------------------------------------------------原文摘录--------------------------------
在曲柄滑块机构的设计中,将x作为设计变量,求出已知滑块行程H,行程速比系数K时机构传力性能最优的x值,使得最小传动角γmin为最大,从而设计出此机构。
机器种类很多,但它们都是由各种机构组成的,曲柄滑块机构就是常用机构之一。它有一个重要特点是具有急回特性。故按行程速比系数K设计具有最优传力性能的曲柄滑块机构是设计中常遇到的问题。本文将x作为设计变量,给出了解决问题的方法。
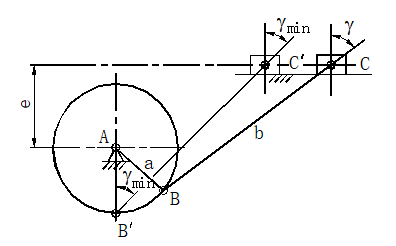
曲柄滑块机构如图1所示,图中AB为曲柄,长度为a,BC为连杆,长度为b,偏心距为e。γ愈大,对机构传动愈有利,它是机构传动性能的重要指标之一,工程上常以γ值来衡量机构的传力性能。
X和最小传动角γmin的关系

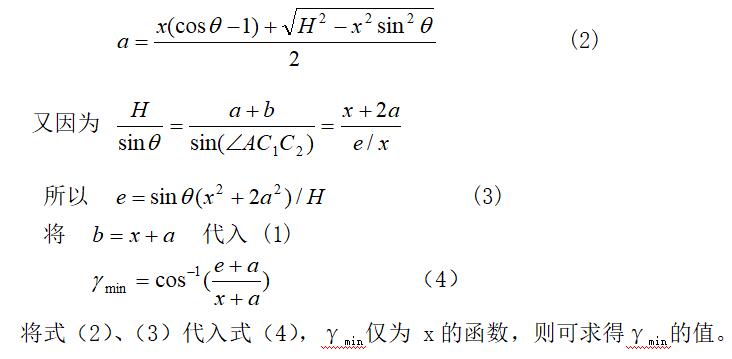
Matlab编程实现最优设计
已知数据:X取值范围为0~627mm,行程H = 650mm,极位夹角等于46°。
第一步:
其实我们要做的非常简单,就是把上图中的(2),(3),(4)公式转化成matlab语句,输出图像,圈取最优解区间,缩小范围,定位最优解。
首先:
X的值是一个取值区间,我们要生成的图像也是一个曲线形式(便于观察),不妨设每一个X对应的值为Y,即Y=(kx^2+bx+c)(x,k,b,c为常数)的一个函数关系。
那么我们必须注意的一点就是一 一对应关系,一个X只能对应一个Y值(搞错的话,matlab会报错),我们可以仿照python中的切片命令,将0~627切成628的小片段(以一个单位长度进行切片),当然也可以切成210、34……这样matlab会按照分开的长度进行汇报数据,也是为了方便下一步观察。
然后
要做的便是如何将公式转化为matlab语句,其实自我感觉matlab和python特别相像,初学者在很短的时间内就可以编译较为复杂的程序,这点和python特别相似,它不像c或c+那般不友好(从入门到放弃……),这里我们只需要注意几个地方。
(此处只是相对于我自己的解题方法)
1..*与 *在matlab中是有区别的,我们计算都是相对于一个矩阵,因为X的待取值组成一个矩阵(1行628列)
2.X(cosd(60)) != X * (cosd(60))注意千万不要省略
3..*cosd(60) = 1/2 cos(60) = -0.95241298041516弧度制和角度制……
代码:
ones_1 = ones(1,628);%生成一个1行210列的全1矩阵
x1 = 0:1:627;%由 Xmax = 行程 / tan(极位夹角) = 627.698 对数组每间隔三个整数取一个计算点
x2 = x1 .* x1 ;%X2 = X1对应数组每个值的平方
b = x1 * (cosd(46) - 1) + sqrt(650 * 650 - x2 * sind(46) * sind(46) );
a1 = b / 2;
a2 = a1 .* a1;%a2 = a1对应数组每个值的平方
e = sind(46) * (x2 + 2 * a2) / 650 ;
fenzi = e + a1;%分子
fenmu = x1 + a1;%分母
fenshu = fenzi ./ fenmu;% .*和*的区别
r = acosd(fenshu);
%全1矩阵除以cos(fenshu) 算出0-627中每个整数对应的 r
% r 最小传动角度
plot(x1 , r);
函数图像,找取极大值
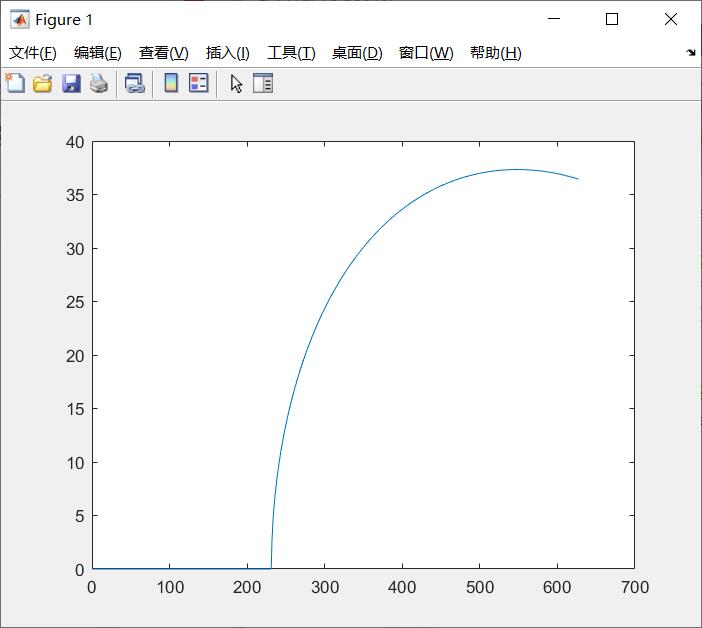
图像只是让我们确定区间,方便定位,本次区间在(500,600)之间
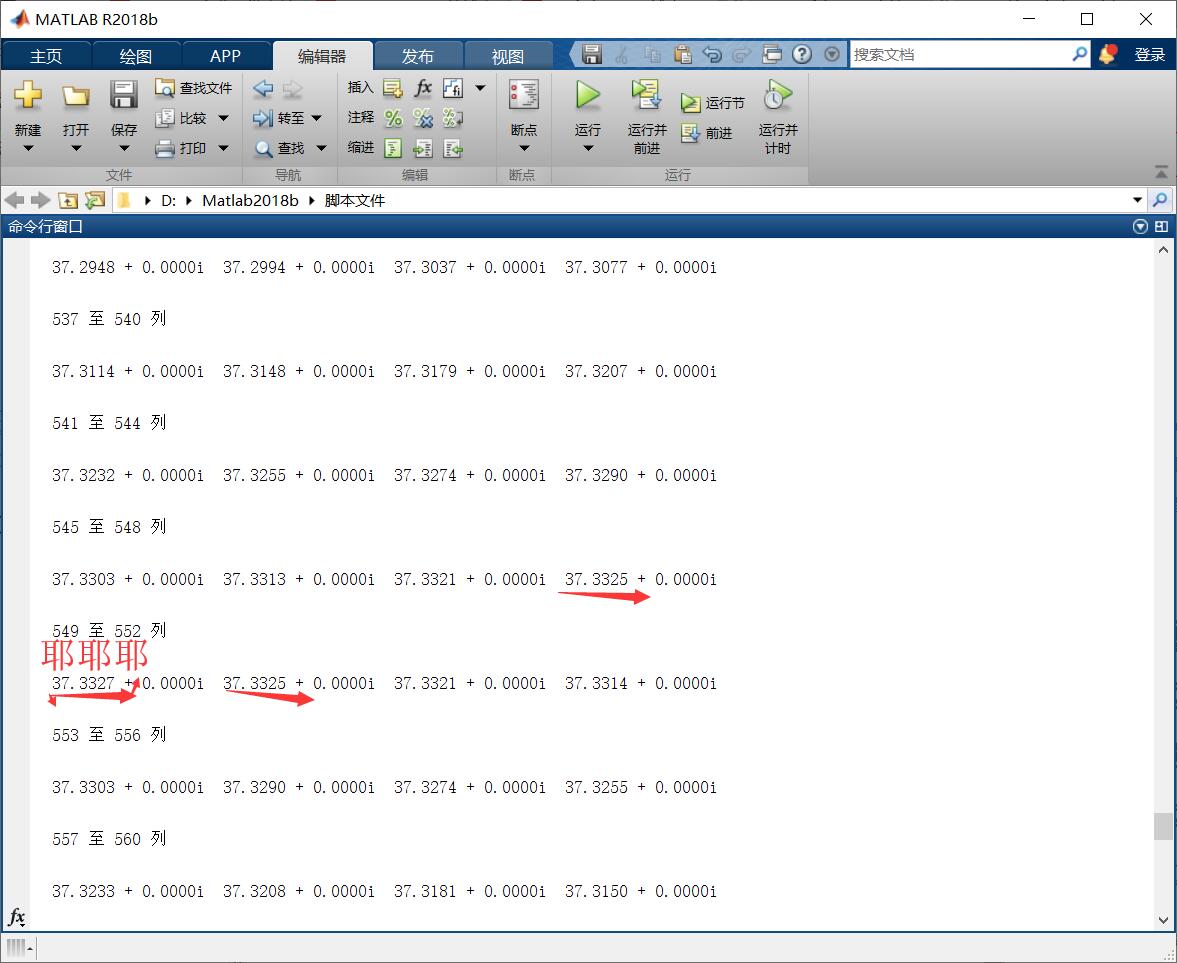
我们可以很清楚的看到,最小传动角的极大值为37.3327,此时我们可知对应的X = 549,则带入程序可求得a,b,e的值

到这就结束了----
能看到最后真的不容易,,,点个赞????????????????????????????????
原文链接
最后
以上就是高挑保温杯最近收集整理的关于Matlab-具有最优传力性能的曲柄滑块机构的设计程序讲解(详细教程)Matlab-具有最优传力性能的曲柄滑块机构的设计程序讲解的全部内容,更多相关Matlab-具有最优传力性能内容请搜索靠谱客的其他文章。








发表评论 取消回复