前缀和应用

86 阅读 0 评论 57 点赞

我是靠谱客的博主殷勤日记本，这篇文章主要介绍前缀和应用，现在分享给大家，希望可以做个参考。

文章目录

- 一维前缀和
- 二维前缀和

定义：前缀和指一个数组的某下标之前的所有数组元素的和（包含其自身）。前缀和分为一维前缀和，以及二维前缀和。前缀和是一种重要的预处理，能够降低算法的时间复杂度。

一维前缀和

一维前缀和的公式：sum[i] = sum[i-1] + arr[i] ; sum是前缀和数组, arr是内容数组。拥有前缀和数组后, 我们可以在O(1)的时间复杂度内求出区间和。

[i, j]的区间和公式: interval [i, j] = sum[j] - sum[i - 1]

leetcode：和为K的子数组

前缀和解决：

首先遍历数组构建前缀和数组，在拥有前缀和数组后，通过双层循环计算数组中每一个子项与之前的子项之间的区间和(子数组的和)。时间复杂度O(n^2)

class Solution {
    public int subarraySum(int[] nums, int k) {
        int len=nums.length;
        int[] preSum=new int[len+1];
        for(int i=0;i<len;i++){
            preSum[i+1]=preSum[i]+nums[i];
        }
        int result=0;
        for(int left=0;left<len;left++){
            for(int right=left;right<len;right++){
                if(preSum[right+1]-preSum[left]==k){
                    result++;
                }
            }
        }
        return result;
    }
}

前缀和+哈希表：

计算完包括了当前数前缀和以后，我们去查一查在当前数之前，有多少个前缀和等于 preSum - k ，这是因为满足 preSum - (preSum - k) == k 的区间的个数是我们所关心的。

public class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0, pre = 0;
        HashMap < Integer, Integer > mp = new HashMap < > ();
        mp.put(0, 1);
        for (int i = 0; i < nums.length; i++) {
            pre += nums[i];
            if (mp.containsKey(pre - k)) {
                count += mp.get(pre - k);
            }
            mp.put(pre, mp.getOrDefault(pre, 0) + 1);
        }
        return count;
    }
}

二维前缀和

leetcode：二维区域和检索 - 矩阵不可变

方法来源于leetcode题解

步骤一：求 preSum

定义 preSum[i] [j]表示从 [0,0] 位置到 [i,j] 位置的子矩形所有元素之和。

可以用下图帮助理解：S(O,D)=S(O,C)+S(O,B)−S(O,A)+D

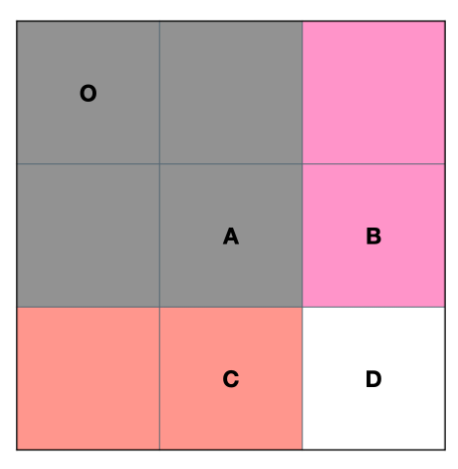
如果求 preSum[i] [j]表示的话，对应了以下的递推公式：

preSum[i] [j]=preSum[i-1] [j]+preSum[i] [j-1]-preSum[i-1] [j-1]+matrix[i] [j]

步骤二：根据 preSum 求子矩形面积

前面已经求出了数组中从 [0,0] 位置到 [i,j] 位置的 preSum。下面要利用 preSum[i] [j]来快速求出任意子矩形的面积。

同样利用一张图来说明：S(A,D)=S(O,D)−S(O,E)−S(O,F)+S(O,G)

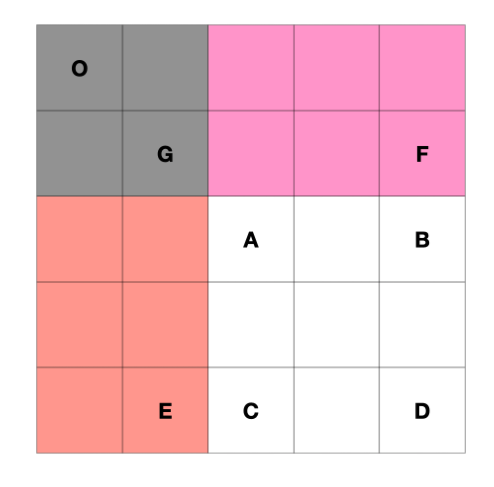
如果要求 [row1, col1] 到 [row2,col2] 的子矩形的面积的话，用 preSum 对应了以下的递推公式：

preSum[row2] [col2]-preSum[row2] [col1-1]-preSum[row1-1] [col2]+preSum[row1-1] [col1-1]

class NumMatrix {
    
    private int[][] preSum;

    public NumMatrix(int[][] matrix) {
        if (matrix.length > 0) {
            preSum = new int[matrix.length + 1][matrix[0].length + 1];
            for (int i = 0; i < matrix.length; i++) {
                for (int j = 0; j < matrix[0].length; j++) {
                    preSum[i+1][j+1] = preSum[i][j+1] + preSum[i+1][j] - preSum[i][j] + matrix[i][j];
                }
            }
        }
    }
    
    public int sumRegion(int row1, int col1, int row2, int col2) {
        return preSum[row2 + 1][col2 + 1] - preSum[row2 + 1][col1] - preSum[row1][col2 + 1] + preSum[row1][col1];
    }
}