编译原理 [0x03][0x02] ==（4.3）语法分析__消除回溯和左递归LL(1)分析法消除回溯

74 阅读 0 评论 49 点赞

我是靠谱客的博主孝顺白羊，最近开发中收集的这篇文章主要介绍编译原理 [0x03][0x02] ==（4.3）语法分析__消除回溯和左递归LL(1)分析法消除回溯，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

消除直接左递归

消除间接左递归

消除左递归的算法

消除回溯

LL(1)分析法

消除直接左递归

例如 $Prightarrow P alpha | beta$ （ $beta$ 不以P开头）表达的是一个 $beta$ 后接任意个 $alpha$

如果要消除左递归，我们可以将其变为右递归

我们引入 ${P}'$ 这个中间量将其转换为

$Prightarrow beta {P}'$

${P}'rightarrow alpha {P}'|varepsilon$

对于多个候选式都含有左递归，我们将其左公因子提出作为P，其余步骤和上面类似

eg:给定文法G(E):

E→E＋T | T

T→T*F | F

F→(E) | i

消除左递归后

G(E):

$Erightarrow T{E}'$

$E{}'rightarrow +T{E}'|varepsilon$

$Trightarrow F{T}'$

$T{}'rightarrow *F{T}'|varepsilon$

$Frightarrow (E))| i$

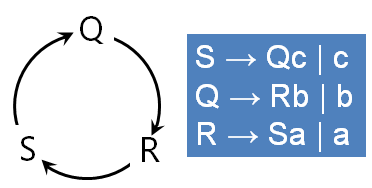
消除间接左递归

给定文法G(S):

S→Qc|c

Q→Rb|b

R→Sa|a

没有直接左递归，但S、Q、R都是左递归的

分析可得，其实这个文法即

S $Rightarrow$ Qc $Rightarrow$ Rbc $Rightarrow$ Sabc

以图表示即

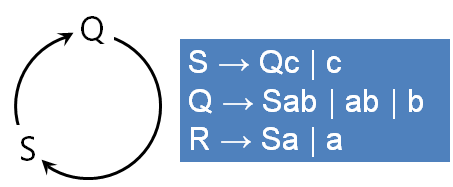
将 Q中的R用R的候选式全部替换，得到

同样的替换S中的Q ，得到

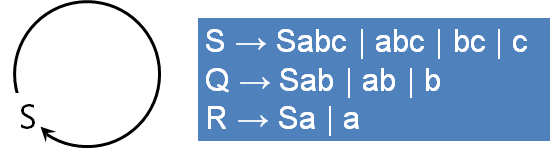
后关于两条Q和R 的候选式没有实际意义可言，删除后即变成上面所说的直接左递归

这时我们消除S的直接左递归，即打破这个了这个圈，即消除了左递归

S → abc $S{}'$ | bc $S{}'$ | c $S{}'$

$S{}'$ → abc $S{}'$ | $varepsilon$

消除左递归的算法

1. 把文法G的所有非终结符按任一种顺序排列 P1，P2，…，Pn；按此顺序执行：

2. FOR i:=1 TO n DO // 把Pi 的规则改造成Pi→a…| Pi+1...| Pi+2...| … | Pi+k...

    BEGIN

         FOR j:=1 TO i-1 DO

             把形如Pi→Pj $gamma$ 的规则改写成 // Pi→a…| Pj+1... | Pj+2...| … | Pj+k...

              Pi→ $delta _{1}$ $gamma$ | $delta _{2}$ $gamma$ | … | $delta _{k}$ $gamma$ ;   (其中Pj→ $delta _{1}$ | $delta _{2}$ | … | $delta _{k}$ 是关于Pj的所有规则) //  Pi→a…| Pi... | Pi+1...| … | Pi+k...

         消除关于Pi规则的直接左递归性

    END //  Pi→a…| Pi+1...| Pi+2...| … | Pi+k...

3. 化简由2所得的文法，去除从开始符号出发永远无法到达的非终结符的产生规则。

消除回溯

为了消除回溯必须保证：

对于文法的任何非终结符，当需要它去匹配输入串时能够根据它所面临的输入符号准确地指派它的一个候选去执行任务，并且此候选的工作结果应该是确定的

那么我们该如何消除回溯呢

PS：消除回溯主要思想：在多个候选中预先知道哪一个候选能得到我们要的句子，就选哪一个候选

FRIST集：First（X）为X的开始符或者首符号集

计算FIRST(X)的方法

如果 X 是终结符号，那么FIRST(X)={X}
如果 X 是非终结符号，

有X->ε，那么ε在FIRST(X)中
且 X -> Y1Y2Y3…Yk 是产生式，则

如果a在FIRST(Yi)中，且 ε 在FIRST(Y1)，FIRST(Y2)，…，FIRST(Yi-1)中，那么a也在FIRST(X)中；

如果ε 在FIRST(Y1)，FIRST(Y2)，…，FIRST(Yk)中，那么ε在FIRST(X)中

书本方法：

FOLLOW集：Follow(X)指的是在某些句型中紧跟在X右边的终结符号的集合

计算Fellow(X)的方法

首先将结束标记 # 放到 FOLLOW(X) 中（当然X得是第一个）
按照下面两个规则进行，直至所有的FOLLOW集合都不再增长为止

如果存在产生式X ->αBβ ，那么 FIRST(β)中所有非ε的符号都在FOLLOW(B)中；
如果存在产生式X ->αB，或者X ->αBβ 且FIRST(β)包含 ε，那么FOLLOW(X)中的所有符号都加入到FOLLOW(B)中

书本方法：

PS：得先求First集合,例如X - -> YZ ,

①将Z的First集中除了 ε 的放入Y的Fellow集中，

②Fellow（X）的都放进Follow（B）

③重复①②直至fellow集不变为止

注意的是：fellow最好从前开始，往后逐步推进，后一个的fellow一般由前一个决定（即Fellow从前往后，First从后往前）