算法笔记_面试题_15.回溯算法模板及示例0. 回溯算法模板1. 组合相关2. 分割相关3. 子集相关

77 阅读 0 评论 51 点赞

我是靠谱客的博主开朗钢笔，最近开发中收集的这篇文章主要介绍算法笔记_面试题_15.回溯算法模板及示例0. 回溯算法模板1. 组合相关2. 分割相关3. 子集相关，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

0. 回溯算法模板

leecode上的相关题目:

1. 组合相关

1.1 组合-77题

1.2 电话号码的字母组合-17题

1.3 组合总和-39题

2. 分割相关

2.1 分割回文串-131题

2.2 复原 IP 地址-93题

3. 子集相关

3.1 不含重复整数的集合的子集(78. 子集)

3.2 含重复整数的数组的子集 (90. 子集 II)

3.3 找出所有子集的异或总和再求和

3.4 统计按位或能得到最大值的子集数目

0. 回溯算法模板

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

适用范围:

几乎所有的搜索问题

根据具体题目可能需要改动的地方:

什么时候输出
哪些情况需要跳过

leecode上的相关题目:

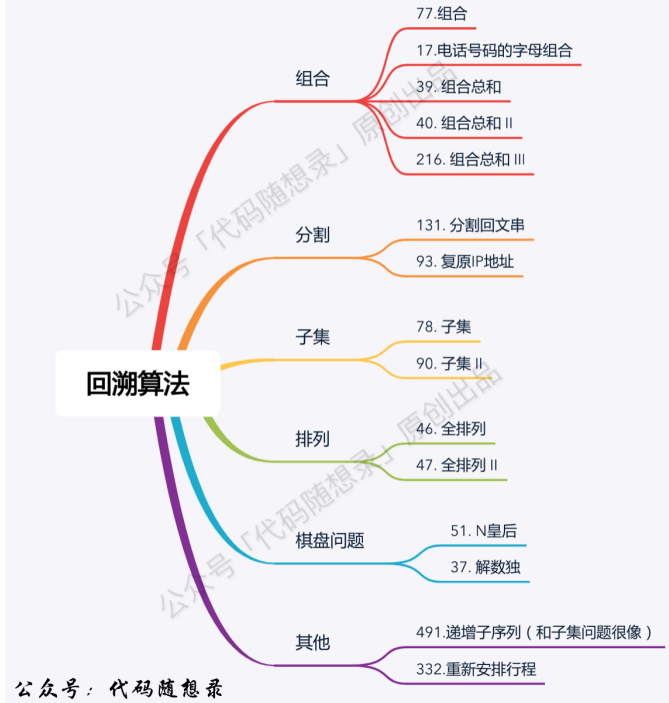
1. 组合相关

1.1 组合-77题

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按任何顺序返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/combinations
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

代码:

class Solution {
public:
    vector<vector<int>> result; //可以定义成成员变量,使函数简洁
    vector<vector<int>> combine(int n, int k) {
        int startIndex = 1;
        vector<int> path;
        backTracking(n, k, path, startIndex);
        return result;
    }
    void backTracking (int n, int k, vector<int> path, int startIndex) {
        if (k == path.size()) {  //终止条件:当子集数量到达k个时,就可以收集起来,然后返回了.
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= n; ++i) { // 为什么用for: 如当选择1时,剩余的[2,3,4], 要依次选择一遍.
            path.push_back(i);  // 为什么是i = startIndex: 如选择2时, 剩余[3,4], 要从3的index开始.这样也避免了重复选择
            backTracking(n, k, path, i+1); //问题规模缩小一位,
            path.pop_back();  //回溯:是为了给其他数字机会, 像出栈一样
        }
    }
};

优化: i <= n-(k-path.size())+1

1. 已经选择的元素个数：path.size();

2. 还需要的元素个数为: k - path.size();

3. 在集合 n中⾄多要从该起始位置 : n - (k - path.size()) + 1，开始遍历

为什么有个 +1 呢，因为包括起始位置，我们要是⼀个左闭的集合。

举个例⼦， n = 4 ， k = 3 ，⽬前已经选取的元素为0（path.size为0 ）， n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。从 2 开始搜索 都是合理的，可以是组合 [2, 3, 4] 。

class Solution {
public:
    vector<vector<int>> result; //可以定义成成员变量,使函数简洁
    vector<vector<int>> combine(int n, int k) {
        int startIndex = 1;
        vector<int> path;
        backTracking(n, k, path, startIndex);
        return result;
    }
    void backTracking (int n, int k, vector<int> current, int startIndex) {
        if (k == path.size()) {  //终止条件:当子集数量到达k个时,就可以收集起来,然后返回了.
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= n-(k-path.size())+1; ++i) { // 为什么用for: 如当选择1时,剩余的[2,3,4], 要依次选择一遍.
            path.push_back(i);  // 为什么是i = startIndex: 如选择2时, 剩余[3,4], 要从3的index开始.这样也避免了重复选择
            backTracking(n, k, path, i+1); //问题规模缩小一位,
            path.pop_back();  //回溯:是为了给其他数字机会, 像出栈一样
        }
    }
};

1.2 电话号码的字母组合-17题

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按任意顺序返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：

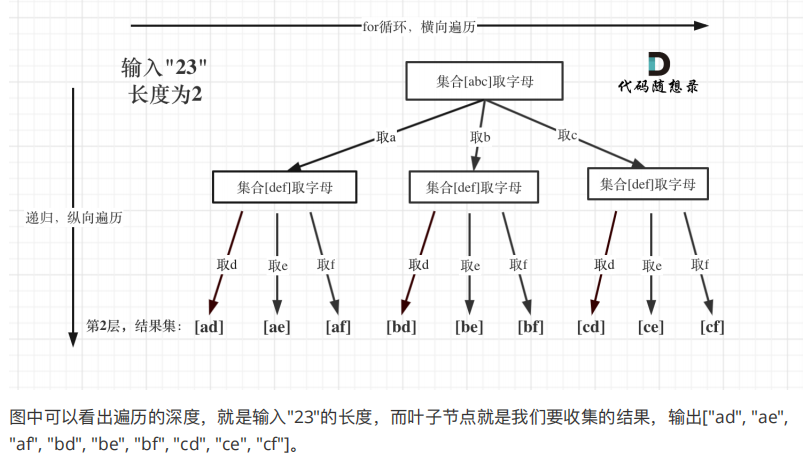
输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

输入：digits = ""
输出：[]

代码及解读:

区别于77题在于, 这里深度遍历的对象虽然仍然是字符的长度,但宽度遍历的对象则是每个数字对应的字符(如2对应的"abc")

class Solution {
public:
    vector<string> res;
    string path;
	
    //疑问:定义成 unordered_map<int, string> 取值使用 phoneMap.at(digits[pos])不通过??? why
	unordered_map<char, string> phoneMap = { 
        {'2', "abc"},
        {'3', "def"},
        {'4', "ghi"},
        {'5', "jkl"},
        {'6', "mno"},
        {'7', "pqrs"},
        {'8', "tuv"},
        {'9', "wxyz"}
    };

    vector<string> letterCombinations(string digits) {
        backTracking(digits, 0);
        return res;
    }
    void backTracking(const string & digits, int pos) {
        if(pos == digits.length()) {
            res.push_back(path);
            return;
        }
        string str = phoneMap.at(digits[pos]); //注意:这里取map中对应的值
        for (int i = 0; i < str.length(); ++i) {//注意:这里遍历的宽度是每个数字对应的字符数量,如"pqrs"是4
            path.push_back(str[i]);
            backTracking(digits, pos+1); //常规操作: 这里遍历的深度是digits的长度,如[2,3,4],深度是3,对应pos+1
            path.pop_back();
        }
    }
};

1.3 组合总和-39题

给定一个无重复元素的正整数数组 candidates 和一个正整数 target ，找出 candidates 中所有可以使数字和为目标数 target 的唯一组合。

candidates 中的数字可以无限制重复被选取。如果至少一个所选数字数量不同，则两种组合是唯一的。

对于给定的输入，保证和为 target 的唯一组合数少于 150 个。

示例 1：

输入: candidates = [2,3,6,7], target = 7
输出: [[7],[2,2,3]]

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

代码:

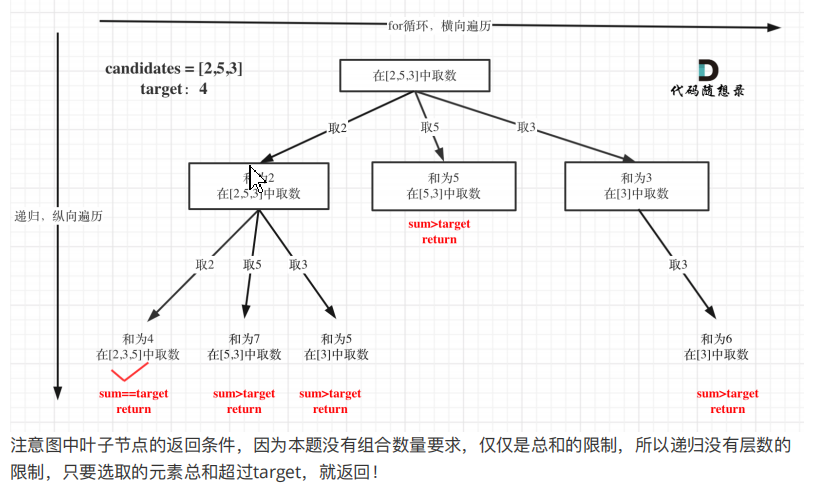
区别与77题, 可以重复选择元素(意味着树的层数没有限制), 所以递归时, 在for循环中, 传入当前index即可,使用for循环自然地遍历到下一个节点.

图示如下:

class Solution {
public:
    vector<vector<int>> res;

    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<int> path;
        backTracking(candidates, target, path, 0);
        return res;
    }
    void backTracking(vector<int>& candidates, int target, vector<int> path, int pos) {
        if (target == 0) {
            res.push_back(path);
            return;
        }
        if(target < 0 || pos == candidates.size()) { //注意:这里的返回条件勿少! //无pos==..也可测试通过, 有第二个条件有所过滤,加速了些
            return;
        }
        for (int i = pos; i < candidates.size(); i++) {
            path.push_back(candidates[i]);
            backTracking(candidates, target-candidates[i], path, i); //注意:这里递归可选择重复元素,所以传入的是i.
            path.pop_back();
        }
    }
};

优化:

若当前的和已经大于target时,那么对于排序的数组,选择后面的值加入,肯定更加大于target,所以,可以使用先排序candidates,然后剪枝的方法进行优化.

class Solution {
public:
    vector<vector<int>> res;

    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<int> path;
        sort(candidates.begin(), candidates.end()); //优化:先从小到大排序
        backTracking(candidates, target, path, 0);
        return res;
    }
    void backTracking(vector<int>& candidates, int target, vector<int> path, int pos) {
        if (target == 0) {
            res.push_back(path);
            return;
        }
        if(target < 0 || pos == candidates.size()) {
            return;
        }
        for (int i = pos; i < candidates.size(); i++) {
            if (target-candidates[i] < 0) { //选择当前值加入都大于目标值,对于排序候选数组,则后面的值就不用加入了.
                return; //这里等价于break
            }
            path.push_back(candidates[i]);
            backTracking(candidates, target-candidates[i], path, i);
            path.pop_back();
        }
    }
};

2. 分割相关

2.1 分割回文串-131题

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是回文串。返回 s 所有可能的分割方案。

回文串是正着读和反着读都一样的字符串。

示例 1：

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

示例 2：

输入：s = "a"
输出：[["a"]]

代码:

class Solution {
public:
    vector<vector<string>> res;
    vector<vector<string>> partition(string s) {
        vector<string> path;
        backTracking(s, path, 0);
        return res;
    }
    void backTracking(const string &s, vector<string> path, int pos) {
        if (pos == s.length()) {
            res.push_back(path);
            return;
        }
        for(int i = pos; i < s.length(); ++i) {
            string currentStr = s.substr(pos, i-pos+1); //注意:[pos, i]之间就是分割的子串
            if(!isPalindrome(currentStr)) { //注意: 不是回文子串,直接跳出该子树
                continue; //注意:这里不是return或者break(break此处等价于return, 跳过了后面所有分支,此处是不合理的), 因为对于aba, ab不是回文,continue过滤掉本分支中其他分割即可,但是下一个分支中aba是回文
            }
            path.push_back(currentStr);
            backTracking(s, path, i+1);
            path.pop_back();
        }
    }
    bool isPalindrome (const string &s) {
        if (s.empty()) 
            return false;
        int start = 0;
        int end = s.length()-1;
        for (int i = start, j = end; i < j; ++i, --j) {
            if (s[start] != s[end])
                return false;
        }
        return true;
    }
};

图示:

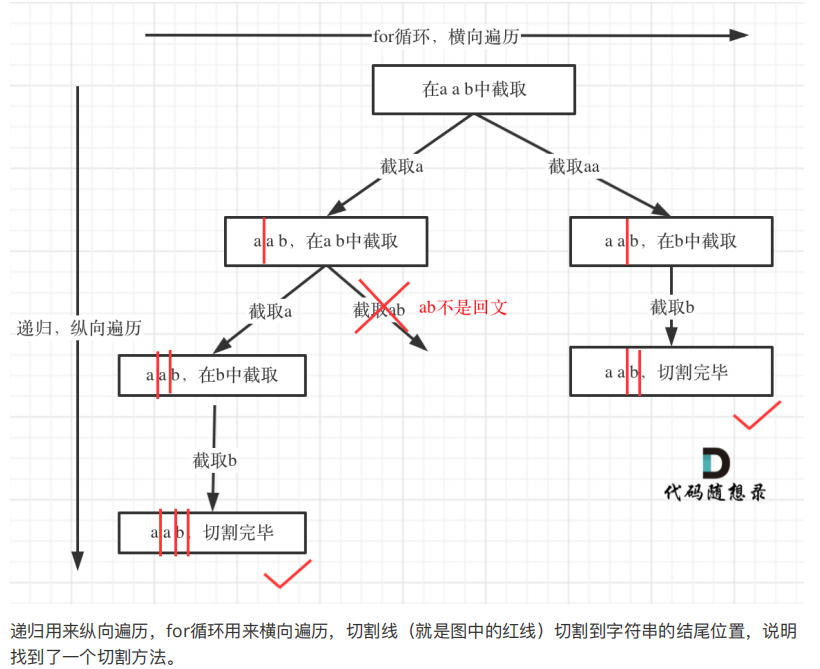
2.2 复原 IP 地址-93题

给定一个只包含数字的字符串，用以表示一个 IP 地址，返回所有可能从 s 获得的有效 IP 地址。你可以按任何顺序返回答案。

有效 IP 地址正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。

例如："0.1.2.201" 和 "192.168.1.1" 是有效 IP 地址，但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是无效 IP 地址。

示例 1：

输入：s = "25525511135"
输出：["255.255.11.135","255.255.111.35"]

示例 2：

输入：s = "0000"
输出：["0.0.0.0"]

代码及解读:

本题于上题分割回文串很类似, 都属于分割问题, 区别于上题的点在于分割的字符串的有效性的判断,以及分割段数是有限制的(只有4段, 意味着深度遍历只需要4层). 其他的还是上述模板.

class Solution {
public:
    vector<string> res;
    vector<string> path;
    vector<string> restoreIpAddresses(string s) {
        int segNum = 0;
        backTracking(s, 0, 0);
        return res;
    }
    void backTracking(string s, int pos, int segNum) {
        if (pos == s.length() && segNum == 4) { //注意: 返回条件, 多了一个segment numuber
            res.push_back(vector2string(path));
            return;
        }
        for(int i = pos; i < s.length(); ++i) {
            if(segNum == 4) { //加速措施: 只深度遍历4层即可 //该if不加也能得到正确结果
                string seg4 = s.substr(pos,s.length()-pos); //注意: 到第4段时,直接取剩下所有的数字,看是否满足有效性
                if (!isValid(seg4)) {
                    return;
                }
            }
            else{
                string seg = s.substr(pos, i-pos+1);
                if (!isValid(seg)) {
                    return; //注意:这里不是contiue, 即该分支无效,在后面再加一位数字更加无效,所有,跳过后面所有的分支, 如 2561111, 256无效, 其后面的分支, 如2561更加无效.
                }
                path.push_back(seg);
                backTracking(s, i+1, segNum+1);
                path.pop_back();
            }
        }
    }
    bool isValid(const string &s) {
        if (s.empty())
            return false;
        int num = atoi(s.c_str()); //这里默认为输入的字符串是可以被分割成有效的ip的,不含@这样的特殊字符
        if (s[0] == '0') { //注意:分两种情况: 第一位是0还是非0
            if(s.size() == 1)
                return true;
            else    
                return false;
        }
        else{
            if( num >=0 && num <=255) {
                return true;
            }
            else
                return false;
        }

    }
    // 拼出一个正确的(含.的)ip出来
    string vector2string(vector<string> path) {
        if (path.size() == 0) 
            return string("");
        string ipStr("");
        for (int i = 0; i < path.size(); ++i) {
            ipStr += path[i];
            if (i < path.size()-1) {
                ipStr += ".";
            }
        }
        return ipStr;
    }
};

其他解法: 参考「代码随想录」带你学透回溯算法！93. 复原 IP 地址

3. 子集相关

3.1 不含重复整数的集合的子集(78. 子集)

给定一个含不同整数的集合，返回其所有的子集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]代码及解读

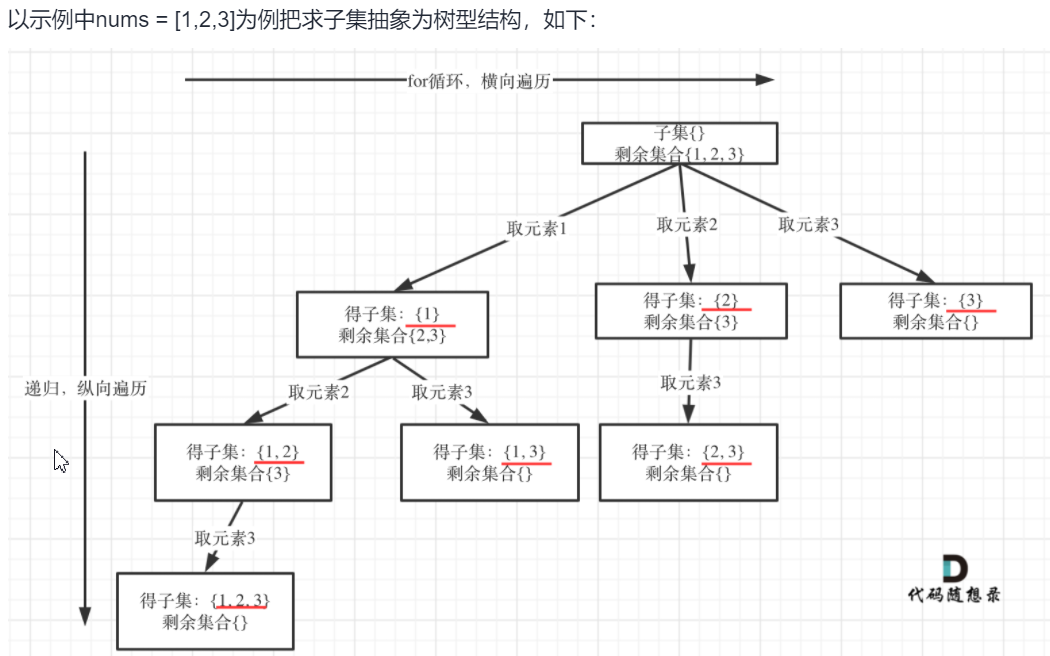
class Solution {
public:
    // 面试点: 中等题, 看候选人是否会使用递归解决问题
    // 知识点关键词: 深度优先遍历, 回溯
    vector<vector<int>> subsets(vector<int> &nums) {
        vector<vector<int>> results;
        vector<int> curNums;
        sort(nums.begin(), nums.end()); //注意: 也可以不sort
        
        subSetsCore(results, nums, curNums, 0);
        
        return results;
    }
    void subSetsCore(vector<vector<int>> & results, const vector<int> &nums, //注意results和curNums是引用传递
                     vector<int> &curNums, int pos) {
        results.push_back(curNums);                     //注意:这里空的也算子集的一部分
        for (int i=pos; i<nums.size(); ++i) {           //特别注意: 搜索开始的位置 i=pos
            curNums.push_back(nums[i]);                 // => 相当于放入[1,]
            subSetsCore(results, nums, curNums, i+1);   //注意 i+1 // => 相当于放入[1,2],[1,3]
            curNums.pop_back();                         // => 回溯,从树根向上遍历删除
        }
    }
};

本题还有一种方法：对于nums中的每一位，都有两种可能，选择或者不选择。所以就采用二进制的方法。设总共有 n 个数字，则总共就有 2^n 种可能（1 << n）。对于每一种可能i, 其二进制对应的位置为1时，我们认为当前要选择，否则认为当前不选择。因此代码如下。特别注意这里的判断条件和运算符优先级：if ( (i & (1 << j)) != 0 ) 。

class Solution {
public:
    vector<vector<int>> subsets(vector<int> &nums) {
        vector<vector<int>> results;
        int n = nums.size();
        if (n == 0) { // 可能省略
            return results;
        }

        for (int i = 0; i < (1 << n); i++) { // 总共有 2^n种可能（n个数， 每个数有两种可能，选择or不选择）//注意是 1<<n
            vector<int> result;
            for (int j = 0; j < n; j++) {
                if ( (i & (1 << j)) != 0) { //依次遍历nums中的3个数, 选择 i 中 二进制中为1的位数，对应的数字，比如 i=0(001) 选择 nums[0]; i=3(011), 选择 nums[0] 和nums[1] //注意 运算符优先级 不等于!= 要优先与 按位与&，要加括号！
                    result.push_back(nums[j]);
                }
            }
            results.push_back(result);
        }

        return results;    
    }
};

3.2 含重复整数的数组的子集 (90. 子集 II)

和上面的代码基本一致, 只需要添加一句代码: 在判断重复添加到数组时跳过即可.

描述: 给定一个可能具有重复数字的列表，返回其所有可能的子集。

示例 1：

输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

示例 2：

输入：nums = [0]
输出：[[],[0]]代码及解读

代码

注意重复数字的过滤条件：if ( i != pos && nums[i] == nums[i-1] ) ，不要写错了。当前循环索引不是第一个，且当前数字等于前一个时，就跳过。

class Solution {
public:
    // 面试点: 中等题, 看候选人是否会使用递归解决问题
    // 知识点关键词: 深度优先遍历, 回溯
    vector<vector<int>> subsetsWithDup(vector<int> &nums) {
        vector<vector<int>> results;
        vector<int> curNums;
        sort(nums.begin(), nums.end()); //注意: 这里需要sort
        
        subsetsWithDupCore(results, nums, curNums, 0);
        
        return results;
    }
    void subsetsWithDupCore(vector<vector<int>> & results, const vector<int> &nums, //注意results和curNums是引用传递
                     vector<int> &curNums, int pos) {
        results.push_back(curNums);                     //注意:这里空的也算子集的一部分
        for (int i=pos; i<nums.size(); ++i) {           //特别注意: 搜索开始的位置 i=pos
            if (i!=pos && nums[i]==nums[i-1]) {         //特殊处理部分: 跳过重复的数字,不添加到候选子集中
                continue;
            }
            curNums.push_back(nums[i]);                 // => 相当于放入[1,]
            subsetsWithDupCore(results, nums, curNums, i+1);   //注意 i+1 // => 相当于放入[1,2],[1,3]
            curNums.pop_back();                         // => 回溯,从树根向上遍历删除
        }
    }
};

3.3 找出所有子集的异或总和再求和

描述:

一个数组的异或总和定义为数组中所有元素按位 XOR 的结果；如果数组为空，则异或总和为 0 。

例如，数组 [2,5,6] 的异或总和为 2 XOR 5 XOR 6 = 1 。
给你一个数组 nums ，请你求出 nums 中每个子集的异或总和，计算并返回这些值相加之和。

注意：在本题中，元素相同的不同子集应多次计数。

数组 a 是数组 b 的一个子集的前提条件是：从 b 删除几个（也可能不删除）元素能够得到 a 。

示例 1：

输入：nums = [1,3]
输出：6
解释：[1,3] 共有 4 个子集：
- 空子集的异或总和是 0 。
- [1] 的异或总和为 1 。
- [3] 的异或总和为 3 。
- [1,3] 的异或总和为 1 XOR 3 = 2 。
0 + 1 + 3 + 2 = 6

示例 2：

输入：nums = [5,1,6]
输出：28
解释：[5,1,6] 共有 8 个子集：
- 空子集的异或总和是 0 。
- [5] 的异或总和为 5 。
- [1] 的异或总和为 1 。
- [6] 的异或总和为 6 。
- [5,1] 的异或总和为 5 XOR 1 = 4 。
- [5,6] 的异或总和为 5 XOR 6 = 3 。
- [1,6] 的异或总和为 1 XOR 6 = 7 。
- [5,1,6] 的异或总和为 5 XOR 1 XOR 6 = 2 。
0 + 5 + 1 + 6 + 4 + 3 + 7 + 2 = 28

代码及解读:

参考：力扣

class Solution {
public:
    int subsetXORSum(vector<int>& nums) { // 比如 nums=[5,1,3]
        int result = 0;

        // 方式1: ok
        // for (int i=0; i<nums.size(); ++i) {         //注意: for循环在递归外,首先加入第1位元素是:[5,...] [1,...] [3,...]
        //     subsetXORSumCore(result, nums, nums[i], i+1); //注意: 这里第3个参数, 第4个参数,从第2位(i+1)开始
        // }
        
        // 方式2: ok
        subsetXORSumCore(result, nums, 0, 0);

        return result;
    }
    
    //pos表示当前要取的nums中的元素的索引
    void subsetXORSumCore(int &result, const vector<int> &nums, int curResult, int pos) { 
        if (pos==nums.size()) {             //做处理,输出
            result += curResult;
        }
        else {
            subsetXORSumCore(result, nums, curResult^nums[pos], pos+1); //添加一个元素, 比如 [5,1,3]进行异或
            subsetXORSumCore(result, nums, curResult, pos+1);           //略过一个元素, 这里 [5,1]进行异或
        }
    }
};

图示:

3.4 统计按位或能得到最大值的子集数目

给你一个整数数组 nums ，请你找出 nums 子集按位或可能得到的最大值，并返回按位或能得到最大值的不同非空子集的数目。

如果数组 a 可以由数组 b 删除一些元素（或不删除）得到，则认为数组 a 是数组 b 的一个子集。如果选中的元素下标位置不一样，则认为两个子集不同。

对数组 a 执行按位或，结果等于 a[0] OR a[1] OR ... OR a[a.length - 1]（下标从 0 开始）。

示例 1：

输入：nums = [3,1]
输出：2
解释：子集按位或能得到的最大值是 3 。有 2 个子集按位或可以得到 3 ：
- [3]
- [3,1]

示例 2：

输入：nums = [2,2,2]
输出：7
解释：[2,2,2] 的所有非空子集的按位或都可以得到 2 。总共有 23 - 1 = 7 个子集。

示例 3：

输入：nums = [3,2,1,5]
输出：6
解释：子集按位或可能的最大值是 7 。有 6 个子集按位或可以得到 7 ：
- [3,5]
- [3,1,5]
- [3,2,5]
- [3,2,1,5]
- [2,5]
- [2,1,5]

代码及解读:

class Solution {
public:
    int count;
    int max;
    int countMaxOrSubsets(vector<int>& nums) {
        count = 0;
        max = 0;
        for (int i = 0; i<nums.size(); ++i) {
            max |= nums[i]; //注意1:一个数组子集中按位或的最大值,等于所有元素的按位或的结果!
        }

        int curResult = 0;
        countMaxOrSubsetsCore(nums, curResult, 0, false); //注意4: 默认chosed状态

        return count;
    }
    void countMaxOrSubsetsCore(const vector<int>& nums, int curResult,
                                int pos, bool chosed) {
        if (curResult == max && chosed) { // 注意2: 统计条件:因为当前轮未选中当前元素的状态,等于上一次选中上一个元素的状态,
             ++count;                     // 所以只统计选中状态时的子集是否满足条件!
        }
        if (pos == nums.size()) {  //注意3: 返回条件!
            return;
        }
        countMaxOrSubsetsCore(nums, curResult | nums[pos], pos + 1, true); //选中状态才进行按位或
        countMaxOrSubsetsCore(nums, curResult, pos + 1, false);
    }
};

图示:

最后

以上就是开朗钢笔为你收集整理的算法笔记_面试题_15.回溯算法模板及示例0. 回溯算法模板1. 组合相关2. 分割相关3. 子集相关的全部内容，希望文章能够帮你解决算法笔记_面试题_15.回溯算法模板及示例0. 回溯算法模板1. 组合相关2. 分割相关3. 子集相关所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：算法面试题
浏览次数：77 次浏览
发布日期：2023-10-23 20:10:40
本文链接：https://www.kaopuke.com/article/k-p-k_13_u_23_o_22_f0_13_j_18_2.html

算法笔记_面试题_15.回溯算法模板及示例0. 回溯算法模板1. 组合相关2. 分割相关3. 子集相关

概述

0. 回溯算法模板

leecode上的相关题目:

1. 组合相关

1.1 组合-77题

1.2 电话号码的字母组合-17题

1.3 组合总和-39题

2. 分割相关

2.1 分割回文串-131题

2.2 复原 IP 地址-93题

3. 子集相关

3.1 不含重复整数的集合的子集(78. 子集)

3.2 含重复整数的数组的子集 (90. 子集 II)

3.3 找出所有子集的异或总和再求和

3.4 统计按位或能得到最大值的子集数目

最后

评论列表共有 0 条评论

发表评论取消回复

算法笔记_面试题_15.回溯算法模板及示例0. 回溯算法模板1. 组合相关2. 分割相关3. 子集相关

概述

0. 回溯算法模板

leecode上的相关题目:

1. 组合相关

1.1 组合-77题

1.2 电话号码的字母组合-17题

1.3 组合总和-39题

2. 分割相关

2.1 分割回文串-131题

2.2 复原 IP 地址-93题

3. 子集相关

3.1 不含重复整数的集合的子集(78. 子集)

3.2 含重复整数的数组的子集 (90. 子集 II)

3.3 找出所有子集的异或总和再求和

3.4 统计按位或能得到最大值的子集数目

最后

相关文章

评论列表共有 0 条评论

发表评论 取消回复

发表评论取消回复