算法设计与分析基础知识

一、算法设计基础

算法是（algorithm）是对特定问题求解步骤的一种描述，是指令的有限序列。

算法的五个特性：

输入：一个算法可以有零个或多个输入。

输出：一个算法有一个输出或多个输出。

有穷性（finiteness）：对于任何合法的输入，算法必须总是能够在有穷时间内完成。

确定性（determinacy）：算法中的每一条指令都必须有确切的含义，并且对于相同的输入只能得到相同的输出。

可行性（feasibility）：算法中的每一条指令都可以通过已经实现的基本操作执行有限次来实现。

“好算法”的特性：正确性（correctness），健壮性（robustness），可理解性（comprehensible），抽象分级（abstract classification），高效性（high efficiency）。

（个人认为可理解性和抽象分级相差不大，都是为了便于理解。）

基本的数据结构

数据结构（data structure）是指相互之间存在一定关系的数据元素的集合。

线性表（linear list）：简称表，是n个数据元素的有限序列。

栈（stack）：是限定仅在一端进行插入和删除操作的线性表。插入和删除都在栈顶进行操作，另一端为栈底。具有后进先出（last in first out）的特性。

队列（queue）：是只允许在一端进行插入操作，在另一端进行删除操作的线性表。插入在队尾，删除在队头。具有先进先出（first in first out）的特性。

树（tree）：是n（n>=0）个节点的有限集合

任意一颗非空树满足以下条件：

1、有且仅有一个特定的成为根（root）的节点。

2、当n>1时，除根节点之外的其余节点被分成m（m>0）个互不相交的有限集合T1,T2,...,Tm，其中每个集合又是一棵树，并称为这个根节点的子树（subtree）。

图（graph）：由n（n>=0）个顶点的有限集合和顶点之间边的集合组成，通常表示为：G=(V,E)，其中，G表示一个图，V是顶点的集合，E是顶点之间边的集合。

算法设计的一般过程

分析问题-->选择算法设计计数-->设计并描述算法-->手工运行算法（调试）-->分析算法的效率-->实现算法-->不断循环过程直到满足需求

算法优化方向：常量计算，算术运算，用位运算代替除法和取模运算，有利于编译优化，优化逻辑运算，合理安排条件表达式的顺序，改善循环结构。

二、算法分析基础

算法的时间复杂度分析是一种事前分析估算的方法，是对算法所消耗资源的一种渐进分析方法。

渐进分析是指忽略具体机器、编程语言和编译器的影响，只关注在输入规模增大时算法运行时间的增长趋势。

输入规模是指输入量的多少，一般可以从问题描述中得知。

基本语句是执行次数与整个算法的执行次数成正比的语句，基本语句对算法运行时间的贡献最大，是算法中最重要的操作。

算法的计算复杂性概念

①　复杂性：所需资源多少

②　算法复杂性：算法运行时所需资源的量

③　时间复杂性：所需时间资源的量T(n)

④　空间复杂性：所需空间资源的量S(n)

评价一个算法的好坏主要是从两个方面：

一是看算法运行所占用的时间。用时间复杂度来衡量，例如：在以下3个程序中，

（1）x=x+1;
（2）for(i=1;i<=n;i++)
        x=x+1;
（3）for(i=1;i<=n;i++)
       for(j=1;j<=n;j++)
	        x++;

语句x=x+1的出现的次数分别为1，n和(n+1)n/2，则这三个程序段的时间复杂度分别为O(1)，O(n)，O(n^2)，分别为常量阶、线性阶和平方阶。

在算法时间复杂度的表示中，还有可能出现的有：对数阶O(log n)，指数阶O(2n)等。C，log n，n，nlog n，n^2，n^3，2^n。

指数阶的算法不是一个好的算法。

二是看算法运行时所占用的空间，即空间复杂度。空间复杂度不如时间复杂度那么重要。

时间复杂性和空间复杂性在一定条件下是可以相互转化的。动态规划法是一种以牺牲空间换取时间的很好算法。

非递归算法时间复杂度分析

算法的时间复杂度是指算法运行所需的时间。

设有一个在抽象机上运行的算法A，I是某次运行时的输入数据，其规模为n，则算法A的运行时间T是n和I的函数，记做T(n,I)。又设在该次运算中抽象机的第i个基本运算Oi的执行次数为βi，1≤i≤m。βi也是n和I的函数，记做βi(n,I)。那么算法A在输入为I时的运行时间是：

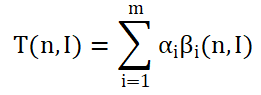
最好、最坏和平均时间复杂度：

最好时间复杂度

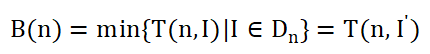
最坏时间复杂度

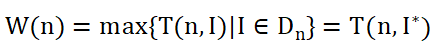
平均时间复杂度

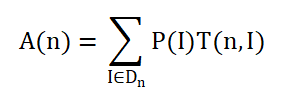
递归算法的时间复杂度分析

扩展递归，扩展就是将地推关系式中等式右边的项根据递推式进行替换，扩展后的项被在此扩展，依此下去，得到一个求和表达式，然后就可以借助于求和技术了。

例，分析下列递推式的时间复杂度：

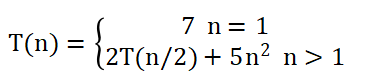
设n=2^k，将递推式扩展

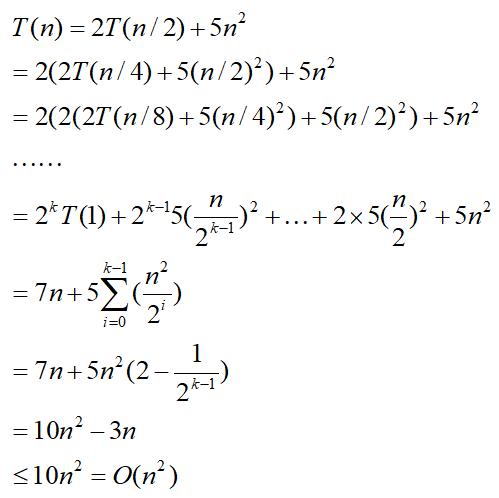
递归算法实际上是一种分而治之的方法，是把复杂问题分解为若干个简单问题来求解，通常满足如下通用分支递推式：

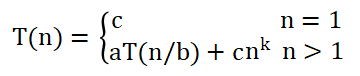
其中a,b,c,k都是常数。这个递推式描述了规模为n的原问题分解为b个规模为n/b的子问题，其中a个子问题需要求解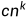，是合并各个子问题的解需要的工作量。

如果T(n)式一个非递减函数，且满足通用分支递推式，则有以下结果成立：

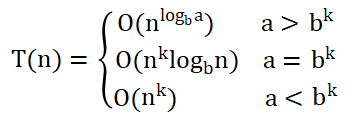
算法的渐进分析

1、若存在两个正的常数c和n0，对于任意n>=n0，都有T(n)<=c*f(n),则称T(n)=O(f(n))。

大O符号用来描述增长率的上限，表示T(n)的增长最多像f(n)增长的那样快，这个上限的阶越低，结果就越有价值。

2、若存在两个正的常数c和n0，对于任意n>=n0，都有T(n)>=c*g(n)，则称T(n)=Ω(g(n))。

大Ω符号用来描述增长率的下限，表示T(n)的增长至少像g(n)增长的那样快，这个上限的阶越高，结果就越有价值。

O(f(n))和Ω(g(n))是一个函数集合，这个函数集合具有同样的增长趋势，f(n)和g(n)只是其中一个函数。

3、若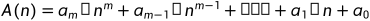是一个m次多项式，则A(n)=O()。

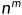参考资料————

算法设计与分析（第3版），王红梅。

https://blog.csdn.net/m0_46316970/article/details/114340309