独立任务最优调度（双机调度）问题

74 阅读 0 评论 49 点赞

我是靠谱客的博主傲娇裙子，最近开发中收集的这篇文章主要介绍独立任务最优调度（双机调度）问题，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

用两台处理机 $A$ 和 $B$ 处理 $n$ 个作业。设 $A$ 和 $B$ 处理第 $k$ 个作业的时间分别为 $a_k$ 和 $b_k$ 。由于各个作业的特点和机器性能的关系，对某些作业，在 $A$ 上的处理时间长；而对另一些作业，在 $B$ 上的处理时间更长。一台处理机在某个时刻只能处理一个作业，而且作业处理是不可中断的，每个作业只能被处理一次。现在要找出一个最优调度方案，使得 $n$ 个作业被这两台处理机处理完毕的时间和最少。

本题是一个独立任务最优调度问题，也被称为双机调度问题，可以利用动态规划的思想解决。当完成 $k$ 个作业时，设机器 $A$ 花费了 $x$ 时间，机器 $B$ 花费时间的最小值肯定是 $x$ 的一个函数。设 $F [k, x]$ 表示完成k个作业且机器 $A$ 花费 $x$ 时间的条件下机器 $B$ 所花费时间的最小值，那么 $F[k, x] = min{F[k-1, x] + b_k, F[k-1, x-a_k]}$ 。其中 $F[k-1, x] + b_k$ 表示第k个作业由机器B来处理，完成前 $k - 1$ 个作业时机器 $A$ 所花费的时间还是 $x$ 。而 $F[k-1,x-a_k]$ 表示第 $k$ 个作业由机器 $A$ 来处理，此时完成前 $k - 1$ 个作业机器A花费的时间是 $x-a_k$ 。

根据 $F$ 的定义，我们知道 $F [n, x]$ 表示完成 $n$ 个作业且机器 $A$ 花费 $x$ 时间的条件下机器 $B$ 所花费时间的最小值。显然， $sumlimits_{k = 0}^{n}a_k$ ，所以对于 $x_i($ 区间 $sumlimits_{k = 0}^{n}a_k]$ 内的任一整数 $)$ ，总有一个 $F[n, x_i]$ 与其对应，那么 $minleft{max{x_i, F[n, x_i]}right}$ 就是最后的结果。由于要处理每个作业 $k$ ，并且处理每个作业 $k$ 的时候都要循环 $sumlimits_{j = 0}^{k}a_j$ 次，所以算法的时间复杂度为 $O(nsumlimits_{k = 0}^{n}a_k)$ 。

考虑以下包含 $6$ 个作业的例子，其中 $a_k={2,5,7,10,5,2}$ ，而 $b_k={3,8,4,11,3,4}$ 。下面对前两个作业进行简单的分析。

	作业1	作业2	作业3	作业4	作业5	作业6
处理机A	2	5	7	10	5	2
处理机B	3	8	4	11	3	4

对于第一个作业，机器$A$所花费时间$x$的取值范围是$0 le x le a_1$。当$xlt0$时，设$F[1,x] = infty$。$x=0$时，$F[1,0]=3$,此时$max(0,F[1,0])=3$，即机器$A$花费$0$时间，机器$B$花费$3$时间；$x=1$时，$F[1,1]=3$，$max(1,F[1,1])=3$；$x=2$时，$F[1,2]=0$，$max(2,F[1,2])=2$，此时作业$1$由机器$A$来处理，花费$2$时间，而机器$B$不处理作业。

对于第二个作业， $x$ 的取值范围是 $a_1 + a_2$ 。当 $x < 0$ 时，同样设 $F [2, x] = \infty$ 。
$x = 0$ ， $F[2,0]=min{F[1,0]+b_2,F[1,0-a_2]}=min{3+8,infty}=11$ ，所以 $m a x (0, 11) = 11$ ；
$x = 1$ ， $F[2,1]=min{F[1,1]+b_2,F[1,1-a_2]}=min{3+8,infty}=11$ ，所以 $m a x (1, 11) = 11$ ；
$x = 2$ ， $F[2,2]=min{F[1,2]+b_2,F[1,2-a_2]}=min{0+8,infty}=8$ ，所以 $m a x (2, 8) = 8$ ；
$x = 3$ ， $F[2,3]=min{F[1,3]+b_2,F[1,3-a_2]}=min{0+8,infty}=8$ ，所以 $m a x (3, 8) = 8$ ；
$x = 4$ ， $F[2,4]=min{F[1,4]+b_2,F[1,4-a_2]}=min{0+8,infty}=8$ ，所以 $m a x (4, 8) = 8$ ；
$x = 5$ ， $F[2,5]=min{F[1,5]+b_2,F[1,5-a_2]}=min{0+8,3}=3$ ，所以 $m a x (5, 3) = 5$ ；
$x = 6$ ， $F[2,6]=min{F[1,6]+b_2,F[1,6-a_2]}=min{0+8,3}=3$ ，所以 $m a x (6, 3) = 6$ ；
$x = 7$ ， $F[2,7]=min{F[1,7]+b_2,F[1,7-a_2]}=min{0+8,0}=0$ ，所以 $m a x (7, 0) = 7$ ；
根据上面的序列，我们可以知道当 $x = 5$ 时，完成两个作业两台机器花费最少的时间为 $8$ ，此时机器 $A$ 花费 $5$ 时间，机器 $B$ 花费 $3$ 时间。此外，还可以看出当 $x lt a_2$ 时，该任务必定由机器 $B$ 处理，因为数组下标小于 $0$ ，是一个不合法的值。
根据上述思路，编写代码如下：

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <limits.h>
#define MAXN 1005

int a[MAXN];//机器A处理各作业的时间
int b[MAXN];//机器B处理各作业的时间
int F[MAXN][MAXN];//
int time[MAXN];//处理作业k所需要的最短时间
int n;

void read() {
    printf("请输入作业数量：");
    scanf("%d",&n);
    printf("请输入机器A处理每个作业的时间：");
    for(int i = 1; i <= n; i++) {
        scanf("%d",&a[i]);
    }
    printf("请输入机器B处理每个作业的时间：");
    for(int i = 1; i <= n; i++) {
        scanf("%d",&b[i]);
    }
}

int min(int x, int y) {
    return x < y ? x : y;
}

int max(int x, int y) {
    return x > y ? x : y;
}

int schedule() {
    int sumA = a[1];
    //k = 1的情况
    for(int x = 0; x < a[1]; x++) {
        F[1][x] = b[1];
    }
    F[1][a[1]] = min(b[1],a[1]);
    //初始化
    for(int i = 2; i <= n; i++) {
        for(int j = 0; j <= n; j++) {
            F[i][j] = INT_MAX;
        }
    }
	//k >= 2的情况
    for(int k = 2; k <= n; k++) {
        sumA += a[k];
        time[k] = INT_MAX;
        for(int x = 0; x <= sumA; x++) {
            if(x < a[k]) {
                F[k][x] = F[k-1][x] + b[k];
            } else {
                F[k][x] = min(F[k-1][x] + b[k], F[k-1][x-a[k]]);
            }
            time[k] = min(time[k],max(x,F[k][x]));
        }
    }
    return time[n];
}

int main(void) {
    read();
    printf("总的最少处理时间为：%dn",schedule());
    return 0;
}

运行结果如下：
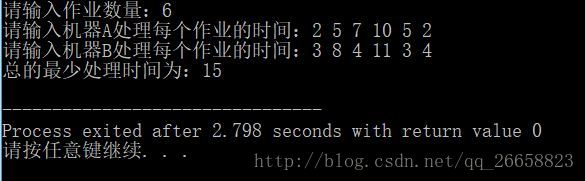
这里写图片描述