首先做这个题需要先复习几组概念：

1. 如果数a能被数b整除，a就叫做b的倍数，b就叫做a的约数。
2. 几个整数中公有的约数，叫做这几个数的公约数；其中最大的一个，叫做这几个数的最大公约数。

举例：

12，16
12的约数有：1，2， 3， 4， 6， 12
16的约数有：1， 2， 4， 8， 16
故而最大的公约数为4。

求最大公约数有多种方法，常见的有辗转相除法。

1. 朴素解——暴力求解

观察性质或者案例，我们可以知道最大公约数一定满足（对于数A和数B来说，最大公约数C），A%C=0且B%C=0。且最大。

那么我们可以从后往前暴力遍历即可，且开始的位置为较小的那个数。

private static int getMaxCommonDivisor(int a, int b) {
    // 使a小,b大
    if(a > b){
        // 两个数交换
        a = a + b;
        b = a - b;
        a = a - b;
    }
    int temp = a;
    while(temp > 0){
        if(a % temp == 0 && b % temp == 0){
            break;
        }
        temp--;
    }
    return temp;
}

这里注意到两个数交换的写法，这里使用的的是加减来做。原理为x = x + y - x，以达到交换目的。
所以数x和数y的交换可以写为：

x = x + y;
y = x - y;
x = x - y;

类似的，在位运算中，可以使用：x = x ^ y ^ x来达到交换的目的，因为异或运算相同为0，故而可以达到。
所以数x和数y的交换可以写为：

x = x ^ y;
y = x ^ y;  // y = x
x = x ^ y;  // x = y

2. 辗转相除法

这里为了直观直接拷贝百度百科的图片：

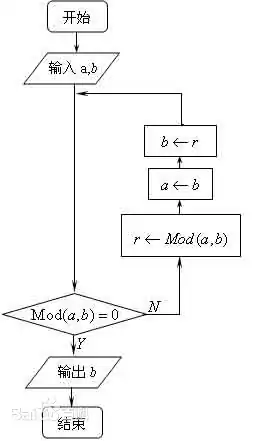
这里举个例子：1997 和 615

• 首先取较大数为被除数，即1997，615为除数，得到余数152；
• 将上轮的除数615作为本轮的被除数，上轮的余数152为本轮的除数，得到余数7；
• 重复这个过程，直到余数为0；
• 此时返回本轮的被除数的值。

故而可以写出如下代码：

private static int getMaxCommonDivisor(int a, int b) {
    // 使 a < b 成立
    if(a > b){
        a = a + b;
        b = a - b;
        a = a - b;
    }
    int yu = 0;
    do{
        yu = b % a;
        b = a;
        a = yu;
    }while (yu != 0);
    return b;
}

最后

以上就是称心蛋挞最近收集整理的关于【Java】求最大公约数1. 朴素解——暴力求解2. 辗转相除法的全部内容，更多相关【Java】求最大公约数1.内容请搜索靠谱客的其他文章。