【算法竞赛入门到进阶】5.3线段树

107 阅读 0 评论 71 点赞

我是靠谱客的博主丰富绿草，最近开发中收集的这篇文章主要介绍【算法竞赛入门到进阶】5.3线段树，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1：HDU 1394 Minimum Inversion Number

先简单回顾一下求逆序对的可能做法：①归并排序；②树状数组/线段树。【例题：洛谷 P1908 逆序对】他们的时间复杂度都是 $O (n l o g n)$ ，但使用的时候要注意树状数组/线段树需要将元素的值离散化。
这个题就相当于给定一个初始的序列，然后问你通过不断把第一个元素移到最后，形成的 $n$ 个序列中，逆序对最少的序列中逆序对的数目。
这个题的关键是在于思考明白这样一个问题：一共有 $n$ 个元素，当前序列第一个元素是第 $k$ 大的元素，很明显形成了 $k - 1$ 个逆序对和 $n - k$ 个顺序对；将第一个元素移到最后，逆序对变成了顺序对，顺序对变成了逆序对。设当前序列的逆序对的个数为 $a n s$ ，则一轮变换后逆序对的个数是 $a n s + = n + 1 - 2 * k$ .
【线段树版本】

#include<bits/stdc++.h>
using namespace std;
const int maxn=5e3+100;
int n,tree[maxn*4],mark[maxn*4],A[maxn];
struct Point{
    int val,id;
    bool operator <(const Point &a)const {return val<a.val;}
}p[maxn];
void Push_down(int p,int len)
{
    mark[p*2]+=mark[p];mark[p*2+1]+=mark[p];
    tree[p*2]+=mark[p]*(len-len/2);tree[p*2+1]+=mark[p]*(len/2);
    mark[p]=0;
}
void Update(int l,int r,int d,int p=1,int cl=1,int cr=n)
{
    if(cr<l || cl>r) return;
    if(cl>=l && cr<=r) tree[p]+=d,mark[p]+=d;
    else{
        int mid=(cl+cr)/2;
        Push_down(p,cr-cl+1);
        Update(l,r,d,p*2,cl,mid);
        Update(l,r,d,p*2+1,mid+1,cr);
        tree[p]=tree[p*2]+tree[p*2+1];
    }
}
int Query(int l,int r,int p=1,int cl=1,int cr=n)
{
    if(cr<l || cl>r) return 0;
    if(cl>=l && cr<=r) return tree[p];
    else{
        int mid=(cl+cr)/2;
        Push_down(p,cr-cl+1);
        return Query(l,r,p*2,cl,mid)+Query(l,r,p*2+1,mid+1,cr);
    }
}
int main()
{
    while(~scanf("%d",&n))
    {
        memset(tree,0,sizeof(tree));
        memset(mark,0,sizeof(mark));
        for(int i=1;i<=n;++i) scanf("%d",&p[i].val),p[i].val++,p[i].id=i;
        sort(p+1,p+n+1);
        for(int i=1;i<=n;++i) A[p[i].id]=i;
        int sum=0;
        for(int i=n;i>=1;--i)
        {
            sum+=Query(1,A[i]-1);
            Update(A[i],A[i],1);
        }
        int minnum=sum;
        for(int i=1;i<n;++i) sum+=n+1-A[i]*2,minnum=min(minnum,sum);
        printf("%dn",minnum);
    }
}

【树状数组版本】

#include<bits/stdc++.h>
#define close ios::sync_with_stdio(false);cin.tie(0);cout.tie(0) 
using namespace std;
const int maxn=5e3+100;
typedef long long ll;
struct Point{
	int val,id;
	bool operator < (const Point &a) const {return val<a.val;}
}p[maxn]; 
int lowbit(int x) {return x&(-x);}
int n,A[maxn],tree[maxn];
void Add(int pos,int num)
{
	for(int i=pos;i<=n;i+=lowbit(i))
		tree[i]+=num;
}
int Query(int pos)
{
	int ans=0;
	for(int i=pos;i;i-=lowbit(i))
		ans+=tree[i];
	return ans;
}
int main()
{
	while(~scanf("%d",&n))
    {
        memset(tree,0,sizeof(tree));
        for(int i=1;i<=n;++i) scanf("%d",&p[i].val),p[i].val++,p[i].id=i;
	    sort(p+1,p+n+1);
        for(int i=1;i<=n;++i) A[p[i].id]=i;
        int sum=0,minnum;
	    for(int i=n;i>=1;--i)
	    {
            sum+=Query(A[i]);
		    Add(A[i],1);
	    }
        minnum=sum;
        for(int i=1;i<n;++i) sum+=n+1-A[i]*2,minnum=min(sum,minnum);
        printf("%dn",minnum);
    }
}

2：HDU 2795 Billboard

题目意思是有一个广告板，尺寸是 $w * h$ ，有 $n$ 个需要粘贴的广告，每个广告的尺寸是 $a_i*1$ ，每个广告的粘贴原则是尽可能地靠近上方、靠近左边粘贴。问每个广告粘贴的行（如果粘贴不下，则输出-1）。
首先明确一件事情，当 $h \leq n$ 时，最多只有 $h$ 行可供我们选择；当 $h > n$ 时，我们最多只用的上 $n$ 行（每行一条广告）。因此二分查找的范围应该是 $[1, m i n (h, n)]$ .二分面临的主要问题是，区间一分为二的时候如何确定递归查找的区间，那么这里可以采用线段树的方式，记录区间最大值，一个区间的最大值比当前广告的长度要长，那就一定能找到一个位置安置。

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+100;
int n,w,h,k,tree[maxn*4];
int Find(int d,int l=1,int r=n,int p=1)
{
    if(l==r){
        tree[p]-=d;
        return l;
    }
    int mid=(l+r)/2,ans;
    if(tree[p*2]>=d) ans=Find(d,l,mid,p*2);
    else ans=Find(d,mid+1,r,p*2+1);
    tree[p]=max(tree[p*2],tree[p*2+1]);
    return ans;
}
int main()
{
    while(~scanf("%d%d%d",&h,&w,&k))
    {
        n=min(h,k);
        for(int i=0;i<4*n+100;++i) tree[i]=w;
        for(int i=1;i<=k;++i)
        {
            int x;scanf("%d",&x);
            if(tree[1]<x) printf("-1n");
            else printf("%dn",Find(x));
        }
    }
}

3：POJ 2828 Buy Tickets

这个题是给定 $n$ 个人，按照顺序每次将第 $i$ 个人放在第 $k$ 个人后面（插队），其余的人则向后移动一位。问最终形成的队伍序列。
最简单的方法，模拟：通过链表的方式去模拟插队的操作，插入所需的时间只有 $O (1)$ ，但是每次寻找第 $k$ 大的元素所需的时间是 $O (n)$ ，因此 $n$ 次操作所需的时间复杂度是 $O(n^2)$ ，对于 $1 \leq N \leq 200000$ 来说一定TLE。
但这个题的核心思想在于反向思维，从最后一个人开始安排，则他的位置不再需要变化。放在第 $k$ 个人后，相当于占据了第 $k + 1$ 个空位，我们用线段树去统计区间的空位数，这样就可以采用二分查找的方式去寻找合适的位置。插入的过程图可参考：https://www.cnblogs.com/CheeseZH/archive/2012/04/29/2476134.html.

#include<iostream>
using namespace std;
const int maxn=2e5+100;
struct Person{
    int val,pos;
}p[maxn];
int n,tree[maxn*4],ans[maxn];
void build(int l=1,int r=n,int p=1)
{
    if(l==r) tree[p]=1;
    else{
        int mid=(l+r)/2;
        build(l,mid,p*2);build(mid+1,r,p*2+1);
        tree[p]=tree[p*2]+tree[p*2+1];
    }
}
void Find(int x,int val,int l=1,int r=n,int p=1)
{
    if(l==r) {ans[l]=val;tree[p]=0;return;}
    int mid=(l+r)/2;
    if(tree[p*2]>=x) Find(x,val,l,mid,p*2);
    else Find(x-tree[p*2],val,mid+1,r,p*2+1);
    tree[p]--;
}
int main()
{
    while(~scanf("%d",&n))
    {
        build();
        for(int i=1;i<=n;++i)  
            scanf("%d%d",&p[i].pos,&p[i].val),p[i].pos++;
        for(int i=n;i>0;--i) Find(p[i].pos,p[i].val);
        printf("%d",ans[1]);
        for(int i=2;i<=n;++i) printf(" %d",ans[i]);
        printf("n");
    }
}

4：POJ 2750 Potted Flower

题意是给定一个 $n$ 个点组成的环，每个点都有一个权值，问能够选取到的连续的一段的和最大是多少。同时还有 $M$ 次对于某个结点值的更新。
对于环的问题，一个常见的解题思路是，复制一倍原数组，线段树我们可以①维护区间最大值，但这样的问题在于有些结点是不合法的，判断起来较为复杂；②维护区间和，但是每次区间和的查询都是 $O (l o g n)$ ，枚举可能的区间就有 $O(n^2)$ ，效率甚至低于暴力。因此这里复制一倍原数组是行不通的。
我们可以直接把一个链拆开，整个链所有结点的和是一定的，我们找到了链上一个区间的最小值，剩下的部分也就成为了不连续的最大值。我们再与链上一个区间的最大值相比较，注意这里题目要求不能选取全部的结点，因此当整个区间的最大值等于整个区间的和（整个序列全为正数），这种情况我们要特判。
我们以求解一个区间的最大值为例，因为是区间和的最大值，而我们处理的时候以 $m i d$ 将整个区间一分为二，分别求解最大值，可能会导致丢失一部分中间连续区间的和的最大值,如图所示：
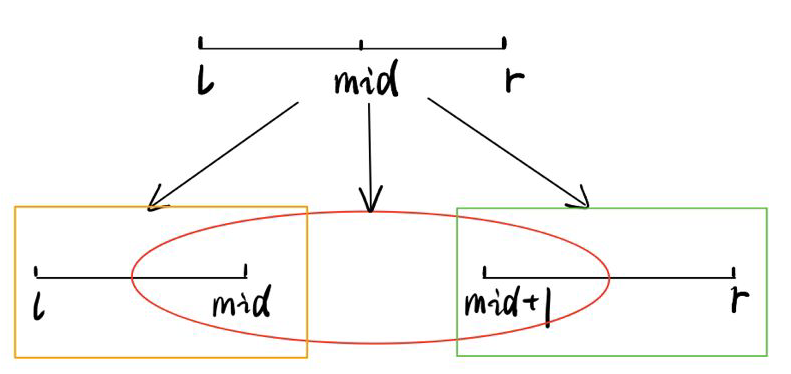
在这里插入图片描述
那我们就要在 $O (1)$ 的时间内得到一个区间内：①包括右端点的连续最大值区间；②包括左端点的连续最大值区间。这样我们可以得到如下的状态转移方程： $s u m [p] = s u m [p * 2] + s u m [p * 2 + 1]$ $l m a x [p] = m a x (l m a x [p * 2], s u m [p * 2] + l m a x [p * 2 + 1])$ $r m a x [p] = m a x (r m a x [p * 2 + 1], s u m [p * 2 + 1] + r m a x [p * 2])$ $t m a x = m a x (m a x (t m a x [p * 2], t m a x [p * 2 + 1]), r m a x [p * 2] + l m a x [p * 2 + 1])$ 最小值同理，这里不做赘述。

#include<iostream>
using namespace std;
typedef long long ll;
const int maxn=1e5+100;
ll n,Q,lmax[maxn*4],rmax[maxn*4],tmax[maxn*4],lmin[maxn*4],rmin[maxn*4],tmin[maxn*4],sum[maxn*4],A[maxn];
void Push_down(ll p)
{
    sum[p]=sum[p*2]+sum[p*2+1];
    lmax[p]=max(lmax[p*2],sum[p*2]+lmax[p*2+1]);
    rmax[p]=max(rmax[p*2+1],sum[p*2+1]+rmax[p*2]);
    tmax[p]=max(max(tmax[p*2],tmax[p*2+1]),rmax[p*2]+lmax[p*2+1]);
    lmin[p]=min(lmin[p*2],sum[p*2]+lmin[p*2+1]);
    rmin[p]=min(rmin[p*2+1],sum[p*2+1]+rmin[p*2]);
    tmin[p]=min(min(tmin[p*2],tmin[p*2+1]),rmin[p*2]+lmin[p*2+1]);
}
void build(ll l=1,ll r=n,ll p=1)
{
	if(l==r) lmax[p]=rmax[p]=tmax[p]=lmin[p]=rmin[p]=tmin[p]=sum[p]=A[l];
	else{
		ll mid=(l+r)/2;
		build(l,mid,2*p);
		build(mid+1,r,2*p+1);
		Push_down(p);
	}
}
void update(ll l,ll r,ll d,ll p=1,ll cl=1,ll cr=n)
{
	if(l>cr || r<cl) return;
	if(cl==cr) lmax[p]=rmax[p]=tmax[p]=lmin[p]=rmin[p]=tmin[p]=sum[p]=d;
	else{
		ll mid=(cl+cr)/2;
		update(l,r,d,p*2,cl,mid);
		update(l,r,d,p*2+1,mid+1,cr);
		Push_down(p); 
	} 
}
int main()
{
	scanf("%lld",&n);
	for(int i=1;i<=n;++i) scanf("%lld",&A[i]);
	build();scanf("%lld",&Q);
	while(Q--)
	{
		ll pos,val;scanf("%lld%lld",&pos,&val);
        update(pos,pos,val);
		if(sum[1]==tmax[1]) printf("%lldn",sum[1]-tmin[1]);
        else printf("%lldn",max(tmax[1],sum[1]-tmin[1]));
	}
}

5：POJ 2886 Who Gets the Most Candies?

题目大意是 $n$ 个孩子，每个孩子手里都有一个数 $A_i$ ，然后每次淘汰一个孩子，下一个被淘汰的孩子取决于当前被淘汰孩子手中的数字：如果 $A_i>0$ ，则下一个淘汰的孩子是当前孩子从左数第 $A_i$ 个；否则，就是当前孩子从右数第 $A_i$ 个。然后，每个孩子得到的糖果数都是他淘汰顺序 $i$ 的约数个数，问能得到最大糖果数以及该孩子的姓名。
变形的约瑟夫问题，但关键在于如何较快地找到下一个被淘汰的孩子。用二分查找的方式，同时采用线段树，快速判断当前区间的孩子数能不能达到需要淘汰的第 $k$ 个。这里为了简单，计算出来的需要被淘汰的第 $k$ 个孩子，都是相对于区间 $[1, n]$ 来说的。
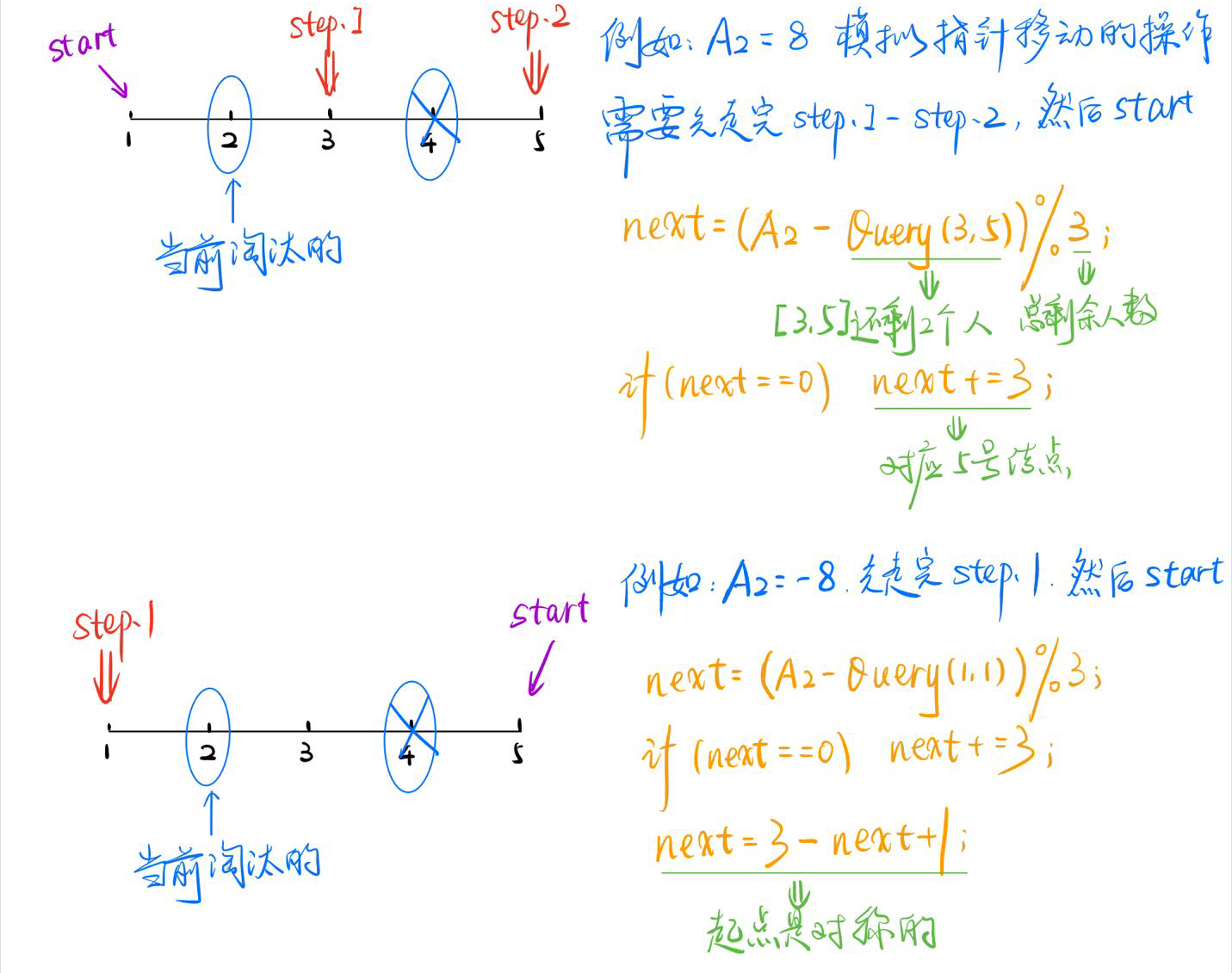在这里插入图片描述然后需要解决的是，如何快速求解 $1$ ~ $n$ 的所有因数的个数。①我们不断枚举可能的因子，一共需要进行操作的次数就是 $nsum_{i=1}^n frac{1}{n}$ ，时间复杂度近似 $O (n l o g n)$ ；②我们可以利用反素数的思想，采用DFS的方式，参考博客：https://blog.csdn.net/ACdreamers/article/details/25049767。

#include<iostream>
#include<cstring>
using namespace std;
const int maxn=5e5+100;
int n,k,id,cur,maxnum,tree[maxn*4],ans[maxn];
typedef long long ll;
struct Person{
    char name[20];
    int num;
}per[maxn];
void Init()
{
    memset(ans,0,sizeof(ans));
    for(int i=1;i<=n;++i)
        for(int j=i;j<=n;j+=i) ans[j]++;
    id=0,maxnum=0;
    for(int i=1;i<=n;++i) if(ans[i]>maxnum) maxnum=ans[i],id=i;
}
void build(int l=1,int r=n,int p=1)
{
    if(l==r) tree[p]=1;
    else{
        int mid=(l+r)/2;
        build(l,mid,p*2);build(mid+1,r,p*2+1);
        tree[p]=tree[p*2]+tree[p*2+1];
    }
}
int Query(int l,int r,int cl=1,int cr=n,int p=1)
{
    if(cl>r || cr<l) return 0;
    if(cl>=l && cr<=r) return tree[p];
    int mid=(cl+cr)/2;
    return Query(l,r,cl,mid,p*2)+Query(l,r,mid+1,cr,p*2+1);
}
int Find(int x,int l=1,int r=n,int p=1)
{
    if(l==r) {tree[p]=0;return l;}
    int mid=(l+r)/2,rec;
    if(x<=tree[p*2]) rec=Find(x,l,mid,p*2);
    else rec=Find(x-tree[p*2],mid+1,r,p*2+1);
    tree[p]=tree[p*2]+tree[p*2+1];
    return rec;
}
int main()
{
    while(~scanf("%d%d",&n,&k))
    {
        
        for(int i=1;i<=n;++i) scanf("%s%d",per[i].name,&per[i].num);
        build();Init();
        for(int i=1;i<=id;++i)
        {
            cur=Find(k);int mod=max(1,n-i);
            if(per[cur].num>0){
                k=((per[cur].num-Query(cur+1,n))%mod+mod)%mod;
                if(k==0) k+=mod;
            }
            else{
                k=((-per[cur].num-Query(1,cur-1))%mod+mod)%mod;
                if(k==0) k+=mod;
                k=n-i-k+1;
            }
        }
        printf("%s %dn",per[cur].name,maxnum);
    }
}

6：POJ 2777 Count Color

题目大意是有两种操作，一种是将区间 $[A, B]$ 刷成第 $k$ 种颜色，另一种是询问区间 $[A, B]$ 有多少种颜色。
这道题的关键在于如何一边进行区间的覆盖，一边统计区间的颜色种数。因为颜色的种类数不超过30，我们可以一个二进制位表示一种颜色，覆盖就是常规的区间覆盖问题，同时能通过区间的或运算计数区间的颜色种类。【同一类型：HDU 5023】

#include<iostream>
using namespace std;
const int maxn=1e5+100;
const int C=1<<30;
int n,k,Q,tree[maxn*4],mark[maxn*4];
typedef long long ll;
void Push_down(int p,int len)
{
    if(mark[p]==0) return;
    mark[p*2]=mark[p*2+1]=1;
    tree[p*2]=tree[p*2+1]=tree[p];
    mark[p]=0;
}
void Update(int l,int r,int d,int cl=1,int cr=n,int p=1)
{
    if(cl>r || cr<l) return;
    if(cl>=l && cr<=r) tree[p]=d,mark[p]=1;
    else{
        int mid=(cl+cr)/2;
        Push_down(p,cr-cl+1);
        Update(l,r,d,cl,mid,p*2);
        Update(l,r,d,mid+1,cr,p*2+1);
        tree[p]=tree[p*2]|tree[p*2+1];
    }
}
int Query(int l,int r,int cl=1,int cr=n,int p=1)
{
    if(cl>r || cr<l) return 0;
    if(cl>=l && cr<=r) return tree[p];
    Push_down(p,cr-cl+1);
    int mid=(cl+cr)/2;
    return Query(l,r,cl,mid,p*2)|Query(l,r,mid+1,cr,p*2+1);
}
int Getans(int x)
{
    int num=0;
    for(unsigned int j=1;j<=C;j*=2)//注意int类型2^31刚好会溢出
        if(x&j) num++;
    return num;
}
int main()
{
    while(~scanf("%d%d%d",&n,&k,&Q))
    {
        for(int i=0;i<n*4+100;++i) tree[i]=1,mark[i]=0;
        while(Q--)
        {
            getchar();
            char op=getchar();
            if(op=='C'){
                int x,y,kind;scanf("%d%d%d",&x,&y,&kind);
                if(x>y) swap(x,y);
                Update(x,y,1<<(kind-1));
            }
            else{
                int x,y;scanf("%d%d",&x,&y);
                if(x>y) swap(x,y);
                printf("%dn",Getans(Query(x,y)));
            }
        }
    }
}

7：HDU 1540 Tunnel Warfare

题目大意是一条直链上有 $n$ 个城市，城市 $i$ 与城市 $i - 1$ 和城市 $i + 1$ 相连（首尾城市除外）。一共有三种操作：①摧毁城市 $x$ ，以及与 $x$ 相连的道路；②查询从城市 $x$ 向左向右出发最远能够达到的城市总数；③修复上一次摧毁的城市。
最简单的想法：二分查找。我们将每次被摧毁的城市加入set中，二分查找到一个城市，满足其 $i d$ 不小于当前城市的 $i d$ （lower_bound()函数）。如果二者相等，说明该城市被摧毁；否则就能根据其扩展的最大区间计算能到达的城市总数。修复城市，就是从set集合中去除掉一个原来被摧毁的城市（erase()函数）。
【二分查找的版本】

#include<bits/stdc++.h>
using namespace std;
const int maxn=5e4+100;
bool vis[maxn];int n,Q;
int main()
{
    while(~scanf("%d%d",&n,&Q))
    {
        memset(vis,0,sizeof(vis));
        stack<int> V_destroy;set<int> cur_status;
        cur_status.insert(n+1);cur_status.insert(0);
        while(Q--)
        {
            getchar();char op=getchar();
            if(op=='D'){
                int num;scanf("%d",&num);
                if(!vis[num]) cur_status.insert(num);
                V_destroy.push(num);vis[num]=1;
            }
            else if(op=='Q'){
                int num;scanf("%d",&num);
                set<int>::iterator it=cur_status.lower_bound(num);
                if(*it==num) printf("0n");
                else printf("%dn",*(it--)-*it-1);
            }
            else{
                if(V_destroy.empty()) continue;
                int cur=V_destroy.top();V_destroy.pop();
                if(!vis[cur]) continue;//城市可能多次摧毁，注意特判
                vis[cur]=0;
                cur_status.erase(cur);
            }
        }
    }
}

这道题同样能使用线段树的解题方式。很明显我们的目标是找到城市 $x$ 所能扩展到的最大区间，也就是左右第一个被破坏的城市。我们可以用两个线段树，分别维护区间最大值&最小值，代表的是一个区间最靠右的被破坏城市（最大值）和一个区间最靠左的被破坏城市（最小值）。当一个城市被破坏的时候，我们就把该结点值更新成这个城市的坐标；当一个城市被修复的时候，我们就把该结点的值恢复成哨兵结点的值。
【线段树的版本】

#include<bits/stdc++.h>
using namespace std;
const int maxn=5e4+100;
int n,Q,tree_max[maxn*4],tree_min[maxn*4],vis[maxn];
void Update_max(int l,int r,int d,int cl=1,int cr=n,int p=1)
{
    if(cl==cr) tree_max[p]=d;
    else{
        int mid=(cl+cr)/2;
        if(l<=mid) Update_max(l,r,d,cl,mid,p*2);
        else Update_max(l,r,d,mid+1,cr,p*2+1);
        tree_max[p]=max(tree_max[p*2],tree_max[p*2+1]);
    }
}
void Update_min(int l,int r,int d,int cl=1,int cr=n,int p=1)
{
    if(cl==cr) tree_min[p]=d;
    else{
        int mid=(cl+cr)/2;
        if(l<=mid) Update_min(l,r,d,cl,mid,p*2);
        else Update_min(l,r,d,mid+1,cr,p*2+1);
        tree_min[p]=min(tree_min[p*2],tree_min[p*2+1]);
    }
}
int Query_max(int l,int r,int cl=1,int cr=n,int p=1)
{
    if(cl>r || cr<l) return 0;
    if(cl>=l && cr<=r) return tree_max[p];
    else{
        int mid=(cl+cr)/2;
        return max(Query_max(l,r,cl,mid,p*2),Query_max(l,r,mid+1,cr,p*2+1));
    }
}
int Query_min(int l,int r,int cl=1,int cr=n,int p=1)
{
    if(cl>r || cr<l) return n+1;
    if(cl>=l && cr<=r) return tree_min[p];
    else{
        int mid=(cl+cr)/2;
        return min(Query_min(l,r,cl,mid,p*2),Query_min(l,r,mid+1,cr,p*2+1));
    }
}
int main()
{
    while(~scanf("%d%d",&n,&Q))
    {
        for(int i=0;i<n*4+100;++i) tree_max[i]=0,tree_min[i]=n+1;
        memset(vis,0,sizeof(vis));
        stack<int> V_destroy;
        while(Q--)
        {
            getchar();char op=getchar();
            if(op=='D'){
                int num;scanf("%d",&num);
                if(!vis[num]) Update_max(num,num,num),Update_min(num,num,num);
                V_destroy.push(num);vis[num]=1;
            }
            else if(op=='Q'){
                int num;scanf("%d",&num);
                int l=Query_max(1,num),r=Query_min(num,n);
                if(l==r) printf("0n");
                else printf("%dn",r-l-1);
            }
            else{
                if(V_destroy.empty()) continue;
                int cur=V_destroy.top();V_destroy.pop();
                if(!vis[cur]) continue;
                vis[cur]=0;
                Update_max(cur,cur,0);Update_min(cur,cur,n+1);
            }
        }
    }
}

8：HDU 1823 Luck and Love

一个非常经典的线段树套线段树。我们可以令树的第一维是高度，第二维是活泼度（虽然活泼度是浮点数，但确保了只有一位，因此可以乘10变换成整数）。对树的操作分为单点更新和区间查询，更新的时候需要注意第一维的更新方式。

#include<bits/stdc++.h>
using namespace std;
int M,tree[220*4][1020*4];
void Sub_update(int l,int r,int val,int id,int flag,int cl=0,int cr=1000,int p=1)
{
	if(cr<l || cl>r) return;
	if(cl==cr){
		//flag是用来判定这个当前的id对应的结点在第一维中是不是满足l==r
		//如果不是需要从一维对应的两个子结点中的子树对应的地方获取值
		if(flag==0) tree[id][p]=max(tree[id][p],val);
		else tree[id][p]=max(tree[id<<1][p],tree[id<<1|1][p]);
	}
	else{
		int mid=(cl+cr)>>1;
		Sub_update(l,r,val,id,flag,cl,mid,p<<1);
		Sub_update(l,r,val,id,flag,mid+1,cr,p<<1|1);
		tree[id][p]=max(tree[id][p<<1],tree[id][p<<1|1]);
	}
}
void update(int l,int r,int d,int val,int cl=100,int cr=200,int p=1)
{
	if(cr<l || cl>r) return;
	if(cl==cr) Sub_update(d,d,val,p,0);
	else{
		int mid=(cl+cr)>>1;
		update(l,r,d,val,cl,mid,p<<1);
		update(l,r,d,val,mid+1,cr,p<<1|1);
		Sub_update(d,d,val,p,1);
	}
}
int Sub_query(int l,int r,int id,int cl=0,int cr=1000,int p=1)
{
	if(cr<l || cl>r) return -1;
	if(cl>=l && cr<=r) return tree[id][p];
	else{
		int mid=(cl+cr)>>1;
		return max(Sub_query(l,r,id,cl,mid,p<<1),Sub_query(l,r,id,mid+1,cr,p<<1|1));
	}
}
int query(int l,int r,int a1,int a2,int cl=100,int cr=200,int p=1)
{
	if(cr<l || cl>r) return -1;
	if(cl>=l && cr<=r) return Sub_query(a1,a2,p);
	else{
		int mid=(cl+cr)>>1;
		return max(query(l,r,a1,a2,cl,mid,p<<1),query(l,r,a1,a2,mid+1,cr,p<<1|1));
	}
}
int main()
{
	while(~scanf("%d",&M))
	{
		if(M==0) break;
		for(int i=0;i<220*4;++i) for(int j=0;j<1020*4;++j) tree[i][j]=-1;
		for(int i=1;i<=M;++i)
		{
			getchar();char op=getchar();
			if(op=='I'){
				int h;double a,l;scanf("%d%lf%lf",&h,&a,&l);
				update(h,h,(int)(10*a),(int)(10*l));
			}else{
				int h1,h2;double a1,a2;scanf("%d%d%lf%lf",&h1,&h2,&a1,&a2);
				if(h1>h2) swap(h1,h2);if(a1>a2) swap(a1,a2);
				int ans=query(h1,h2,(int)(a1*10),(int)(a2*10));
				if(ans==-1) printf("-1n");
				else printf("%.1fn",ans/10.0);
			}
		}
	}
}

9：HDU 4027 Can you answer these queries?

一个非常经典的开方线段树。关键在于一个小于 $2^{63}$ 的数最多开6次平方根就会变成1，以后的开放操作对答案没有任何影响。如何判断一个区间里的数是否有必要继续开方，就在于判断这个区间的和是否等于区间的元素个数。【同一题：洛谷 SP2713】

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+100;
typedef long long ll;
ll n,Q,A[maxn],tree[maxn*4];
void build(int l=1,int r=n,int p=1)
{
    if(l==r) tree[p]=A[l];
    else{
        int mid=(l+r)/2;
        build(l,mid,p*2);build(mid+1,r,p*2+1);
        tree[p]=tree[p*2]+tree[p*2+1];
    }
}
void Update(int l,int r,int cl=1,int cr=n,int p=1)
{
    if(cl>r || cr<l) return;
    if(cl==cr) tree[p]=sqrt(tree[p]);
    else if(tree[p]==cr-cl+1) return;
    else{
        int mid=(cl+cr)/2;
        Update(l,r,cl,mid,p*2);Update(l,r,mid+1,cr,p*2+1);
        tree[p]=tree[p*2]+tree[p*2+1];
    }
}
ll Query(int l,int r,int cl=1,int cr=n,int p=1)
{
    if(cl>r || cr<l) return 0;
    if(cl>=l && cr<=r) return tree[p];
    else{
        int mid=(cl+cr)/2;
        return Query(l,r,cl,mid,p*2)+Query(l,r,mid+1,cr,p*2+1);
    }
}
int main()
{
    int casenum=1;
    while(~scanf("%lld",&n))
    {
        for(int i=1;i<=n;++i) scanf("%lld",&A[i]);
        build();
        printf("Case #%d:n",casenum++);
        scanf("%lld",&Q);
        while(Q--)
        {
            int op,x,y;scanf("%d%d%d",&op,&x,&y);
            if(x>y) swap(x,y);
            if(op==0) Update(x,y);
            else printf("%lldn",Query(x,y));
        }
        printf("n");
    }
}

10：HDU 3333 Turing Tree

这个题的关键是如何对不同的数字进行计数，我们可以先将询问都保存下来，按照r从小到大排序，然后对于出现的相同的数字仅保留最后出现的位置，这样就能保证结果的正确性。

#include<bits/stdc++.h>
#define close ios::sync_with_stdio(false)
using namespace std;
const int maxn=3e4+100;
map<int,int> mp;
typedef long long ll;
ll n,A[maxn],ans[100010],tree[maxn<<2];
struct Query{
	int l,r,id;
	bool operator < (const Query& a)const {return r<a.r;}
}q[100010];
void update(int l,int r,ll d,int cl=1,int cr=n,int p=1)
{
	if(cr<l || cl>r) return;
	if(cl==cr) tree[p]+=d;
	else{
		int mid=(cl+cr)>>1;
		update(l,r,d,cl,mid,p<<1);
		update(l,r,d,mid+1,cr,p<<1|1);
		tree[p]=tree[p<<1]+tree[p<<1|1];
	}
}
ll query(int l,int r,int cl=1,int cr=n,int p=1)
{
	if(cr<l || cl>r) return 0;
	if(cl>=l && cr<=r) return tree[p];
	else{
		int mid=(cl+cr)>>1;
		return query(l,r,cl,mid,p<<1)+query(l,r,mid+1,cr,p<<1|1);
	} 
}
int main()
{
	close;int T;cin>>T;
	while(T--)
	{
		memset(tree,0,sizeof(tree));mp.clear();cin>>n;
		for(int i=1;i<=n;++i) cin>>A[i];
		int Q;cin>>Q;
		for(int i=1;i<=Q;++i) cin>>q[i].l>>q[i].r,q[i].id=i;
		sort(q+1,q+Q+1);
		int cur=1;
		for(int i=1;i<=Q;++i)
		{
			while(cur<=q[i].r){
				update(cur,cur,A[cur]);
				if(mp.find(A[cur])!=mp.end()) update(mp[A[cur]],mp[A[cur]],-A[cur]);
				mp[A[cur]]=cur;cur++;
			}
			ans[q[i].id]=query(q[i].l,q[i].r);
		}
		for(int i=1;i<=Q;++i) cout<<ans[i]<<endl;
	}
}

11：HDU 5869 Different GCD Subarray Query

12：POJ 2528 Mayor’s posters

13：POJ 3225 Help with Intervals

最后

以上就是丰富绿草为你收集整理的【算法竞赛入门到进阶】5.3线段树的全部内容，希望文章能够帮你解决【算法竞赛入门到进阶】5.3线段树所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：算法竞赛入门到进阶——高级数据结构
浏览次数：107 次浏览
发布日期：2023-10-28 09:40:21
本文链接：https://www.kaopuke.com/article/k-p-k_13_u_23_o_18_fw_12__23_c2.html

【算法竞赛入门到进阶】5.3线段树

概述

1：HDU 1394 Minimum Inversion Number

2：HDU 2795 Billboard

3：POJ 2828 Buy Tickets

4：POJ 2750 Potted Flower

5：POJ 2886 Who Gets the Most Candies?

6：POJ 2777 Count Color

7：HDU 1540 Tunnel Warfare

8：HDU 1823 Luck and Love

9：HDU 4027 Can you answer these queries?

10：HDU 3333 Turing Tree

11：HDU 5869 Different GCD Subarray Query

12：POJ 2528 Mayor’s posters

13：POJ 3225 Help with Intervals

最后

评论列表共有 0 条评论

发表评论取消回复

【算法竞赛入门到进阶】5.3线段树

概述

1：HDU 1394 Minimum Inversion Number

2：HDU 2795 Billboard

3：POJ 2828 Buy Tickets

4：POJ 2750 Potted Flower

5：POJ 2886 Who Gets the Most Candies?

6：POJ 2777 Count Color

7：HDU 1540 Tunnel Warfare

8：HDU 1823 Luck and Love

9：HDU 4027 Can you answer these queries?

10：HDU 3333 Turing Tree

11：HDU 5869 Different GCD Subarray Query

12：POJ 2528 Mayor’s posters

13：POJ 3225 Help with Intervals

最后

相关文章

评论列表共有 0 条评论

发表评论 取消回复

发表评论取消回复