语音信号处理基础（七）——短时频域分析

原理

1.短时傅里叶变换

短时傅里叶分析（Short Time Fourier Analysis，STFA）适用于分析缓慢时变信号的频谱分析，在语音分析处理中已经得到广泛应用。其方法是先将语音信号分帧，再将各帧进行傅里叶变换。每一帧语音信号可以被认为是从各个不同的平稳信号波形中截取出来的，各帧语音的短时频谱就是各个平稳信号波形频谱的近似。

由于语音信号是短时平稳的，因此可以对语音进行分帧处理，计算某一帧的傅里叶变换，这样得到的就是短时傅里叶变换。其定义为
$$X_n\left({\mathrm{e}}^{\mathrm{j}\omega }\right)=\sum _{m=-\infty }^{\infty }x(m)w(n-m){\mathrm{e}}^{-\mathrm{j}\omega m}$$
式中,x(n)为语音信号序列;w(n)为实数窗序列,n取不同值时,窗w(n-m)沿时间轴滑动到不同的位置，取出不同的语音帧进行傅里叶变换。
显然,短时傅里叶变换是时间n和角频率w的函数,它反映了语音信号的频谱随时间变化的特性.

短时傅里叶变换有两种不同的解释:

一种是当n固定不变,X,(e)为序列w(n一m)x(m)(-∞<m<∞)的标准傅里叶变换,此时X,(ejw)具有与标准傅里叶变换相同的性质;

另一种是当w固定不变,可以将Xn(ejw)视为信号x(n)与窗函数指数加权w(n)e(jwn)的卷积,此时可以把短时傅里叶变换看做线性滤波
$$\begin{array}{rl}{X}_n\left({\mathrm{e}}^{\mathrm{i}\omega }\right)& =\sum _{m=-\infty }^{\infty }w(m)x(n-m){\mathrm{e}}^{-\mathrm{j}\omega (n-m)}\\ & ={\mathrm{e}}^{-\mathrm{j}\omega n}\left[[w(n){\mathrm{e}}^{\mathrm{j}\omega n}\right]\ast x(n)]\end{array}$$
虽然严格说语音的傅里叶变换并不存在，但是语音加窗后相当于突出了n附近的语音波形而对其他部分加以削弱，当m处于窗函数的有限区间以外时，w（n-m）=0。这样，可以有理由假定窗内的语音特性能够延伸到窗外。比如语音为浊音时，可以认为w（n-m）x（m）序列是从周期性持续的浊音中选出来的；当窗内的语音为清音时，也可以假定窗外也存在同样特性的清音；当语音为爆破音等暂态语音时，还可以直接假定窗外的信号为零。

由于Xn(ejw)相当于信号谱X(ejw)与窗函数谱的卷积,因此应该使窗函数的频谱分辨率高,主瓣尖锐;同时还要使旁瓣衰减大,这样与信号卷积时的频谱泄漏才会少。

①矩形窗、海宁窗和汉明窗的主瓣狭窄且旁瓣衰减较大，具有低通的性质。主瓣的宽度与u成正比，w与窗长成反比，所以窗越长主瓣越窄，加窗后的频谱能够更好地逼近短时语音的频谱。
②窗长越长，频谱分辨率越高，但由于长窗的时间平均作用导致时间分辨率相应下降。
例如，共振峰在不同的基音周期是要发生变化的，但如果使用较长的窗，则会模糊这种变化。
③窗长越短，时间分辨率越高，但频率分辨率相应降低。例如，采用短窗可以清楚地观察到共振峰在不同基音周期的变化情况，但基频以及谐波的精细结构在短时频谱图上消失了。
④由于时间分辨率和频率分辨率的相互矛盾关系，在进行短时傅里叶变换时，应根据分析的目的来折中选择窗长。

2.语谱图表示与实现方法

语谱仪是把语音的电信号送人一组频率依次相接的窄带滤波器中，各个窄带滤波器的输出经整流均方后按频率由低到高的顺序记录在一卷记录纸上。信号的强弱由记录在纸上的灰度来表示。如果某个滤波器输出的信号强，相应的记录将浓黑；反之，则浅淡一些。记录纸按照一定的速度旋转，相当于按不同的时间记录了相应的滤波器输出。由此得到的图形就是语音信号的语谱图，其水平方向是时间轴，垂直方向是频率轴，图上的灰度条纹代表各个时刻的语音短时谱。语谱图反映了语音信号的动态频谱特性，被称为可视语音

例：画出了一段女声“我，到，北，京，去”的语谱图（使用海宁窗函数）。

实现代码

%画出一段语音信号的语谱图
clear all; clc; close all;

[x,Fs]=audioread('C2_2_y.wav');     % 读入数据文件
wlen=200; inc=80; win=hanning(wlen);% 设置帧长，帧移和窗函数
N=length(x); time=(0:N-1)/Fs;       % 计算时间
y=enframe(x,win,inc)';              % 分帧
fn=size(y,2);                       % 帧数
frameTime=(((1:fn)-1)*inc+wlen/2)/Fs; % 计算每帧对应的时间
W2=wlen/2+1; n2=1:W2;
freq=(n2-1)*Fs/wlen;                % 计算FFT后的频率刻度
Y=fft(y);                           % 短时傅里叶变换

clf                                 % 初始化图形

% 画出语音信号的波形  
axes('Position',[0.07 0.72 0.9 0.22]);
plot(time,x,'b');
xlim([0 max(time)]);
xlabel('时间/s'); ylabel('幅值');
title('语音信号波形');

% 画出语谱图      
set(gcf,'Position',[20 100 600 500]);            
axes('Position',[0.1 0.1 0.85 0.5]);  
imagesc(frameTime,freq,abs(Y(n2,:))); % 画出Y的图像  
axis xy; ylabel('频率/Hz');xlabel('时间/s');
title('语谱图');

%设置语谱图的颜色参数
m = 64;
LightYellow = [0.6 0.6 0.6];
MidRed = [0 0 0];
Black = [0.5 0.7 1];
Colors = [LightYellow; MidRed; Black];
%色图表，由m*3组成的矩阵，
%它的每一行是RGB三元组。输出变量cm是色图，
%直接放在colormap函数中就定义了MATLAB中每个图形窗的着色图按cm定制
colormap(SpecColorMap(m,Colors));

①语音信号是实数,在FFT后的频谱是满足共轭对称的，在画频谱时只需取FFT时nfft长的一半就可以了.在程序中FFT的长度就是帧长,所以有

w2-wlen/2+1;n2=1:W2;

freg=(n2-1)*Es/wlen;   %计算FET后的频率刻度

imagesc(frameTime,freq,abs(Y(n2,:)));%画出Y的图像

计算频率刻度和画频谱图都只取帧长的一半.
@在程序中调用了SpecColorMap函数,它是一个设置绘制谱图彩色板的函数。

运行结果

如果需要观察语音谐波的细节，则需要提高语谱图的频率分辨率，也就是减小窗函数的带通宽度。由于带通宽度是与窗长成反比的，因此提高频率分辨率必须要增加窗长。这种情况下得到的语谱图称为窄带语谱图。

例：画出了一段女声“我，到，北，京，去”在不同带宽情况下的语谱图（使用海宁窗函数）。

实现代码

%画出一段语音信号在不同带宽下，也就是在不同的窗长下的语谱图
clear all; clc; close all;

[x,Fs]=audioread('C2_2_y.wav');     % 读入数据文件
wlen=128; inc=32; win=hanning(wlen);% 设置帧长，帧移和窗函数
N=length(x); time=(0:N-1)/Fs;       % 计算时间
y=enframe(x,win,inc)';              % 分帧
fn=size(y,2);                       % 帧数
frameTime=(((1:fn)-1)*inc+wlen/2)/Fs; % 计算每帧对应的时间
W=wlen/2+1; n=1:W;
freq=(n-1)*Fs/wlen;                 % 计算FFT后的频率刻度
Y=fft(y);                           % 短时傅里叶变换
%改变窗长
wlen1=256; inc1=64; win1=hanning(wlen1);% 设置帧长，帧移和窗函数，窗长为400
N=length(x); time=(0:N-1)/Fs;            % 计算时间
y1=enframe(x,win1,inc1)';                % 分帧
fn1=size(y1,2);                          % 帧数
frameTime1=(((1:fn1)-1)*inc1+wlen1/2)/Fs; % 计算每帧对应的时间
W1=wlen1/2+1; n1=1:W1;
freq1=(n1-1)*Fs/wlen1;                % 计算FFT后的频率刻度
Y1=fft(y1);                           % 短时傅里叶变换
%改变窗长
wlen2=512; inc2=128; win2=hanning(wlen2);% 设置帧长，帧移和窗函数
N=length(x); time=(0:N-1)/Fs;         % 计算时间
y2=enframe(x,win2,inc2)';              % 分帧
fn2=size(y2,2);                       % 帧数
frameTime2=(((1:fn2)-1)*inc2+wlen2/2)/Fs; % 计算每帧对应的时间
W2=wlen2/2+1; n2=1:W2;
freq2=(n2-1)*Fs/wlen2;                % 计算FFT后的频率刻度
Y2=fft(y2);                           % 短时傅里叶变换

clf                                 % 初始化图形

% Plot the STFT result              % 画出语谱图
subplot(311)
imagesc(frameTime,freq,abs(Y(n,:))); % 画出Y的图像  
axis xy; ylabel('频率/Hz');xlabel('时间/s');
title('语谱图a');
subplot(312)
imagesc(frameTime1,freq1,abs(Y1(n1,:))); % 画出Y的图像  
axis xy; ylabel('频率/Hz');xlabel('时间/s');
title('语谱图b');
subplot(313)
imagesc(frameTime2,freq2,abs(Y2(n2,:))); % 画出Y的图像  
axis xy; ylabel('频率/Hz');xlabel('时间/s');
title('语谱图c');

运行结果

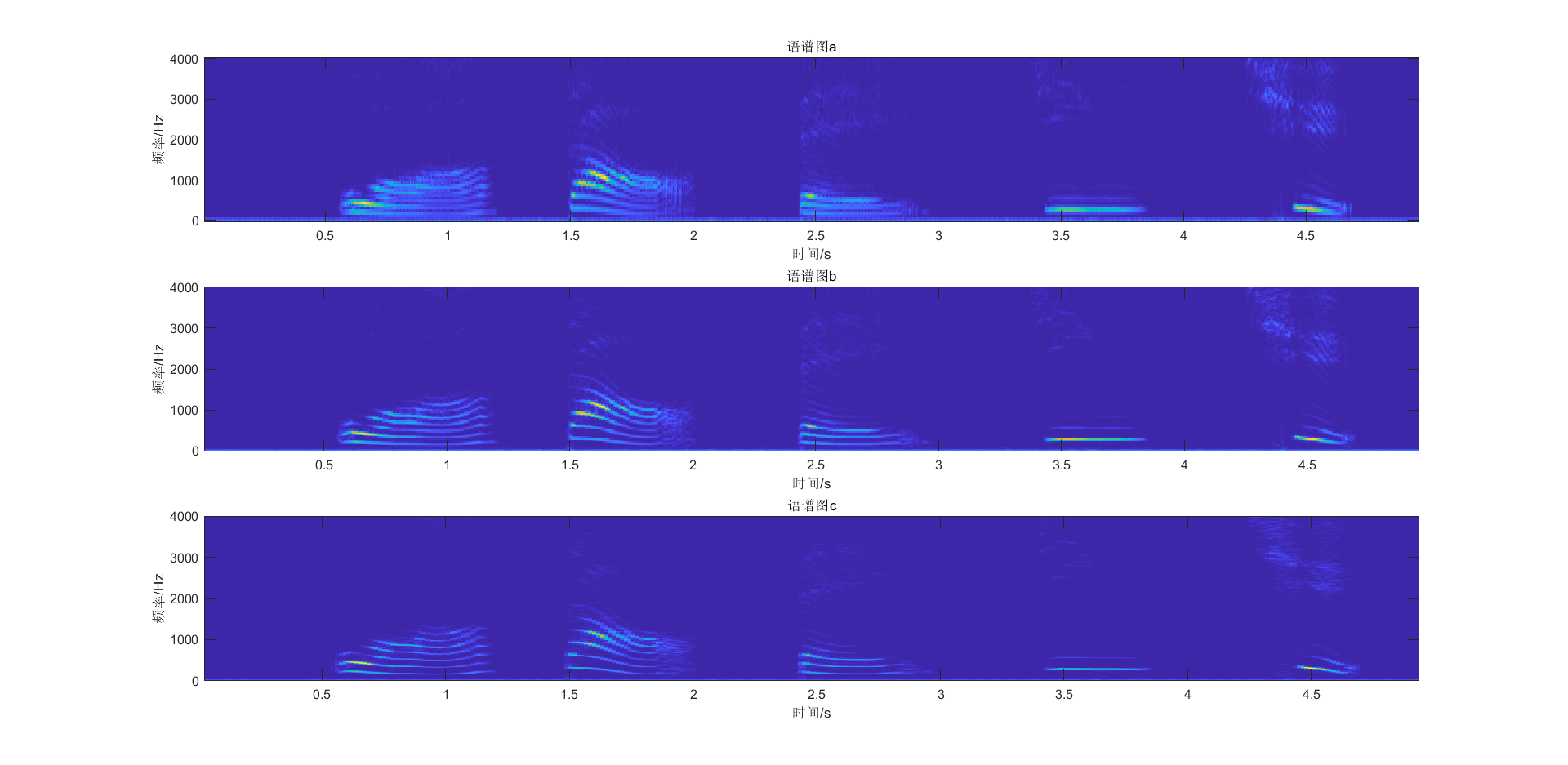
由于宽带语谱图可以获得较高的时间分辨率，反映频谱的快速时变过程；而窄带语谱图可以获得较高的频率分辨率，反映频谱的精细结构。两者相结合，可以提供大量与语音特性有关的信息。语谱图上因其不同的灰度，形成不同的纹路，称之为“声纹”。声纹因人而异，因此可以在司法、安全等场合得到应用。

最后

以上就是认真黑猫为你收集整理的语音信号处理基础（七）——短时频域分析的全部内容，希望文章能够帮你解决语音信号处理基础（七）——短时频域分析所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。