第一章 矩阵与线性方程组（八 ）

一、随机向量的统计描述

1.均值向量

随机向量的最重要统计运算为数学期望。考查m x1随机向量$x(\xi )=[x_1(\xi )，x_2(\xi ),\dots ,x_m(\xi ){]}^T$。令随机变量$x_i(\xi )$的均值$E{x}_i(\xi )={\mu }_i$，则随机向量的数学期望称为均值向量，记作${\mu }_x$，定义为

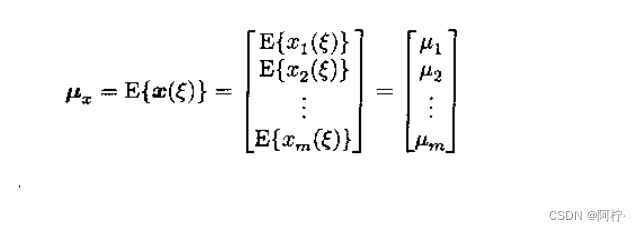
式中，数学期望定义为

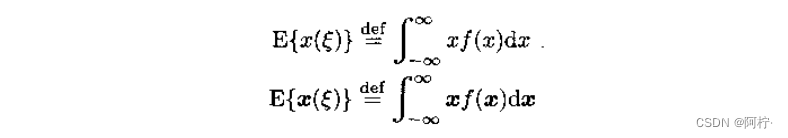
均值向量的元素是随机向量各个元素的均值。

2.相关矩阵与协方差矩阵

均值向量是随机向量的一阶矩，它描述随机向量的元素围绕其均值的散布情况。L均值向量不同，随机向量的二阶矩为矩阵，它描述随机向量分布的散布情况。
随机向量的自相关矩阵定义为

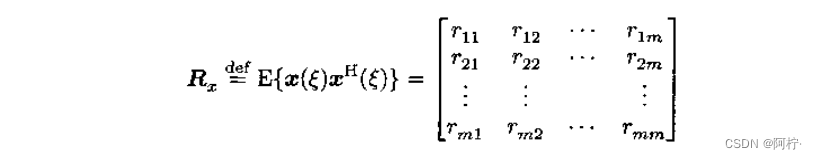
式中，$r_{ii},i=1,2,\dots ,m$表示随机变量$x_i(\xi )$的自相关函数，定义为

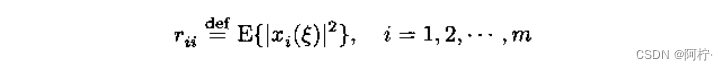
而$r_{ij}$表示随机变量$x_i(\xi )$和$x_j(\xi )$之间的互相关函数，定义为

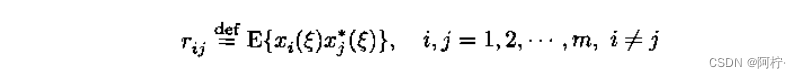
显然，自相关矩阵是共轭对称的，即为 Hermitian矩阵。
随机向量$x(\xi )$的自协方差矩阵定义为

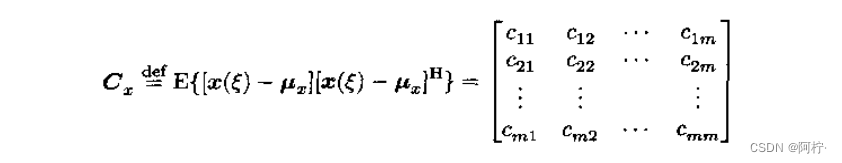
式中，主对角线的元素

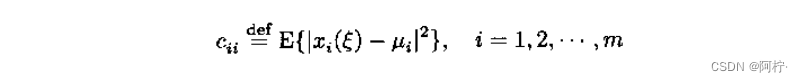
表示随机变量$x_i(\xi )$的方差${\sigma }_i^2$，即$c_{ii}={\sigma }_i^2$，而非主对角线元素

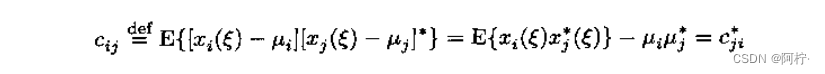
表示随机变量$x_i(\xi )$和$x_j(\xi )$之间的协方差。自协方差矩阵也是 Hermitian矩阵。
自相关矩阵和自协方差矩阵之间存在下列关系:
$$C_x=R_x-{\mu }_x{\mu }_x^H$$

推广自相关矩阵和自协方差矩阵的概念，则有随机向量$x(\xi )$和$y(\xi )$的互相关矩阵

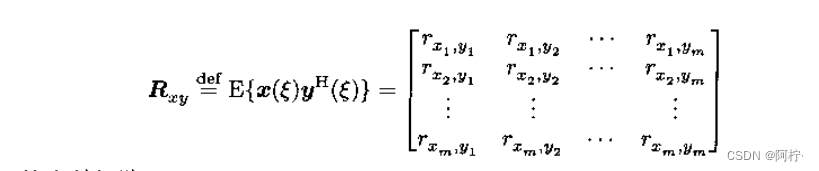
和互协方差矩阵

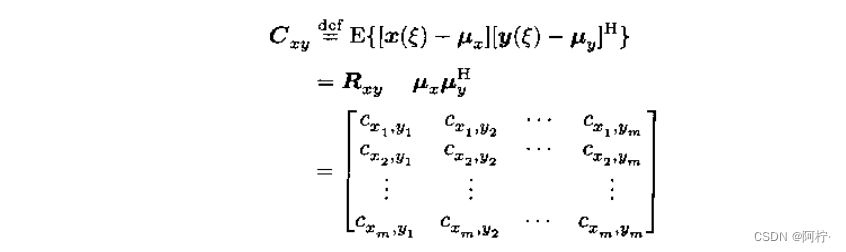
式中，

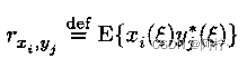
是随机变量$x_i(\xi )$和$y_j(\xi )$之间的互相关，$c_{x_i{y}_j}$是随机变量$x_i(\xi )$和 $y_j(\xi )$之间的互协方差。

• 一个随机向量的白相关矩阵和自协方差矩阵均为正方的共轭对称矩阵
• 两个维数不同的随机向量的互相关矩阵和互协方差矩阵是非正方的矩
• 即使随机向量$x(\xi )$和$y(\xi )$维数相同，互相关矩阵和互协方差矩阵为正方矩阵，但它们也不是共轭对称的。

最后

以上就是结实短靴为你收集整理的矩阵分析与应用+张贤达第一章 矩阵与线性方程组（八 ）一、随机向量的统计描述的全部内容，希望文章能够帮你解决矩阵分析与应用+张贤达第一章 矩阵与线性方程组（八 ）一、随机向量的统计描述所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。