01
知识框架
02
知识点详解
1
二叉排序树
①定义与性质:
二叉排序树(BST),也称二叉搜索树,或二叉查找树。它要么是一颗空树,要么就是具有如下性质的二叉树:
(1)若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(2) 若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(3) 任意节点的左、右子树也分别为二叉查找树;
Tips:如果输出二叉排序树的中序遍历序列,则这个序列是非递减(非递增)有序的,若题目不做特别说明,排序二叉树结点关键字按左小右大分布。
②基本算法:
01
查找关键字
思路:
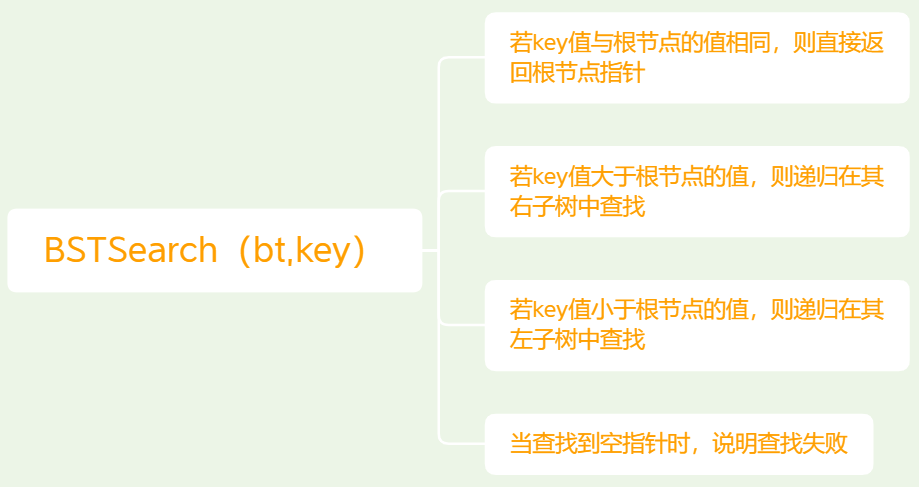
从上述查找过程我们可以看出,二叉排序树的查找算法与折半查找算法类似。折半查找的判定树实际上就是一颗二叉排序树。
代码实现:BTNode* BSTSearch (BTNode* bt, int key){ if (bt==NULL) { return NULL; //查找不成功返回NULL } else { if (bt->key==key) return bt; //等于根结点中的关键字,查找成功,返回关键字所在的结点指针 else if (keykey) return BSTSearch (bt->lchild,key) ;/ /小于根结点中的关键字时到左子树中查找 else return BSTSearch (bt->rchild,key) ; //大于根结点中的关键字的时候到右子树中查找 }}02
插入关键字
思路:
二叉查找树的插入算法比较简单。若二叉排序树为空树,就首先生成根节点;不是空树就按照查找的算法,先找到其父节点,然后作为叶子节点插入,如果值已经存在就插入失败。插入成功返回1,插入失败返回0。
代码实现:
int BSTInsert (BTNode *&bt, int key){ if (bt==NULL){//当前为空指针时说明找到插入位置,创建新结点进行插入 { bt= (BTNode* ) malloc (sizeof (BTNode)) ;//创建新结点 bt->lchild=bt->rchild=NULL; bt->key=key; return 1 ;//将待插关键字存入新结点内,插入成功,返回1 } else {//如果结点不空,则查找插入位置,这部分和查找算法类似 if (key==bt->key) return 0;//关键字已存在于树中,插入失败,返回0 else if(keykey) return BSTInsert (bt->1child, key) ; else return BSTInsert (bt->rchild, key) ; }}03
删除关键字
思路:

有些学校不考关于删除二叉排序树某关键字的算法,大家根据自己的实际情况选看下文代码实现部分。
代码实现:void DeleteNode(BTNode &root,int x){ if(root == NULL){ return; //二叉排序树为空,直接return } if(root->key>x){ DeleteNode(root->lchild,x);//遍历到的结点值比所给值大,就需要遍历左子树 }else if(root->key DeleteNode(root->rchild,x);//遍历到的结点值比所给值小,就需要遍历右子树 }else{ //查找到了删除节点,左子树或者右子树为空只需要将剩下的左子树或者右子树换到待删除结点上即可 if(root->lchild == NULL){ //左子树为空 BiTree tempNode = root; root = root->rchild; free(tempNode); }else if(root->rchild == NULL){ //右子树为空 BiTree tempNode = root; root = root->lchild; free(tempNode); }else{//左右子树都不为空 //一般的删除策略是左子树的最大值点或右子树的最小值点,代替该结点 //这里采用查找左子树最大数据来代替,最大是在左子树的最右边那个结点 BiTree tempNode = root->lchild;//找左子树 if(tempNode->rchild!=NULL){ tempNode = tempNode->rchild;//找左子树的右子树 } root->key = tempNode->key;//将右子树的值赋给需要删除的那结点 DeleteNode(root->lchild,tempNode->key);//删除右子树 } }}2
平衡二叉树
①定义与性质:
平衡二叉树(AVL)实际上就是一颗二叉排序树,它的左右子树高度之差的绝对值不超过1。 平衡因子(bf)为左子树的高度减去右子树的高度,故平衡二叉树的平衡因子为-1或0或1。②平衡二叉树的插入
在构建一棵平衡二叉树的过程中,当有新的节点要插入时,检查是否因插入后而破坏了树的平衡,如果是,则需要做旋转去改变树的结构。先找到插入路径上离插入结点最近的平衡因子的绝对值大于1的结点A,再对以A为根的子树,在保持二叉排序树特性的前提下,调整各结点的位置关系,使之重新达到平衡。下面来介绍集中调整方法。
01
LL旋转(右单旋转)
原因:
在某结点的左孩子的左子树上插入了新的结点,导致平衡二叉树失去平衡。解决方案:
右单旋转调整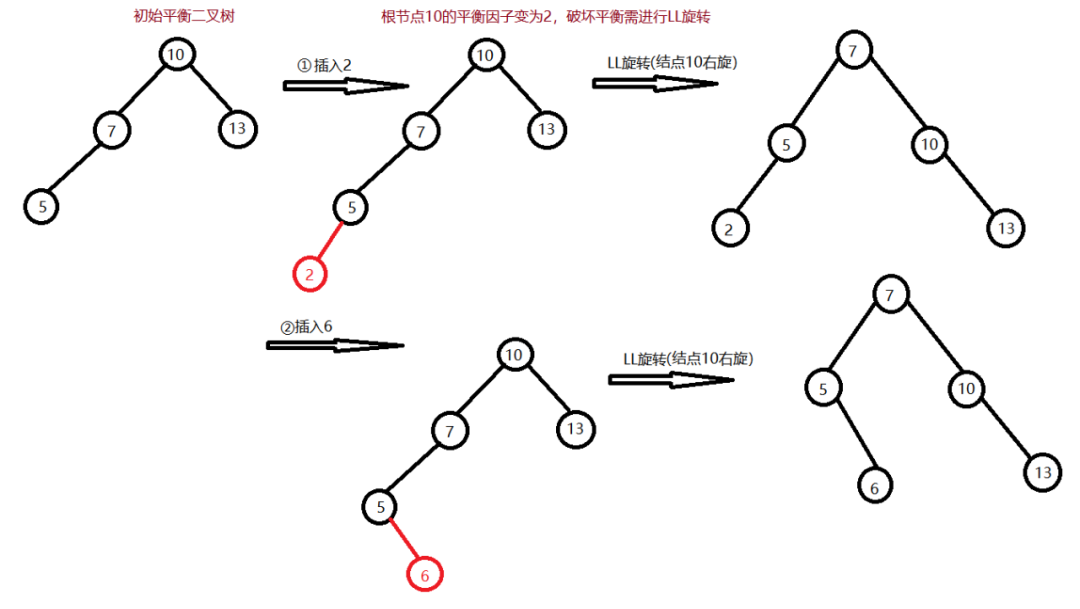
02
RR旋转(左单旋转)
原因:
在某结点的右孩子的右子树上插入了新的结点,导致平衡二叉树失去平衡。解决方案:
左单旋转调整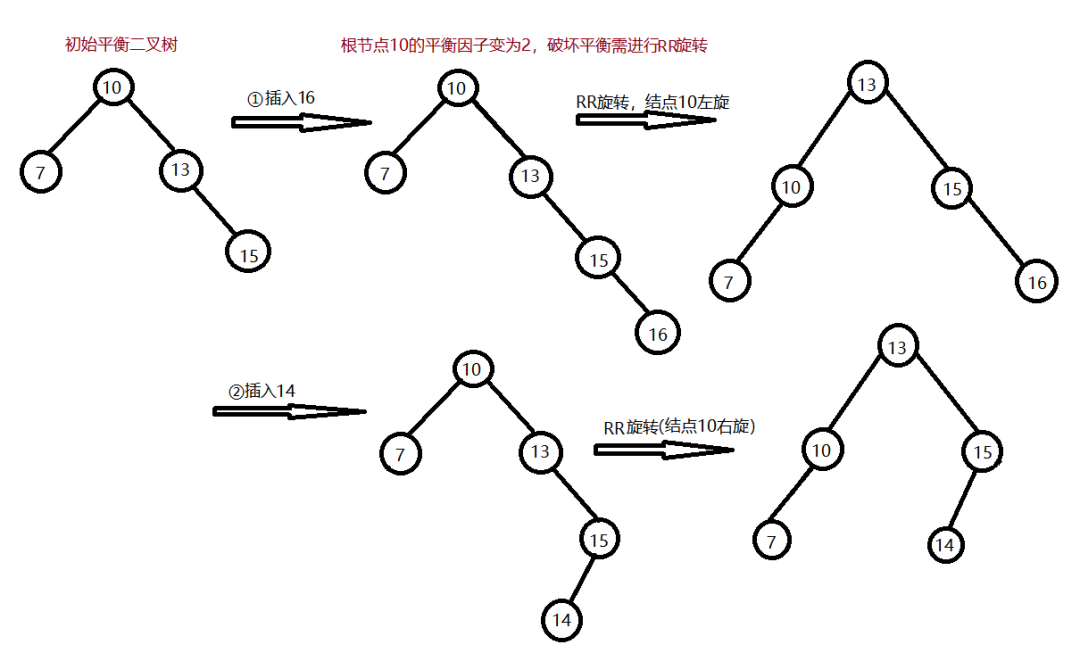
03
LR旋转(先左后右双旋转)
原因:
在某结点的左孩子的右子树上插入了新的结点解决方案:
先左旋转后右旋转
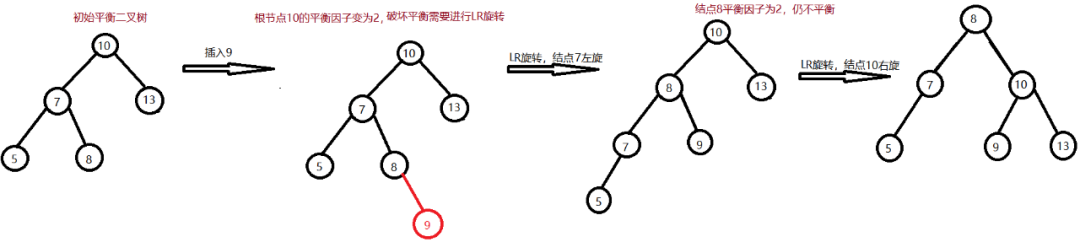
04
RL旋转(先右后左双旋转)
原因:
在某结点的右孩子的左子树上插入了新的结点解决方案:
先右旋转后左旋转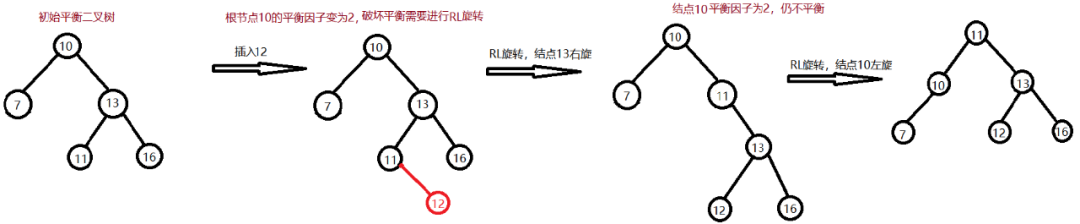
03
相关例题
01
下述二叉树中,哪一种满足性质:从任一结点出发到根的路径上所经过的结点序列按其关键字有序()
A、二叉排序树
B、哈夫曼树
B、AVL树
D、堆
(点击选项查看答案)
Tips:二叉排序树只有中序遍历结果是一个有序序列;在哈夫曼树中所有的关键字只出现在叶结点上,其非叶结点上并没有关键字值;AVL树实际上也是一颗二叉排序树;02
在平衡二叉树中插入一个结点后造成了不平衡,设最低的不平衡结点为A,并已知A的左孩子的平衡因子为0右孩子的平衡因子为1,则应作()型调整以使其平衡。
A、LL
B、LR
C、RL
D、RR
(点击选项查看答案) Tips:A是最低的不平衡点,A的左孩子的平衡因子为0,右孩子的平衡因子为1,如果插入一个节点,变成不平衡,因而只能在右孩子的左孩子插入结点。这样就是A的右孩子平衡因子变化为2。即插入结点的位置符合的是“右左”。因而需要做RL调整。03
试编写一个算法,判断给定的的二叉树是否是二叉排序树
算法思想:二叉排序树的特点:左子树根结点值中序遍历二叉排序树时,得到的序列是一个严格递增的序列。所以我们可以以此来判断二叉树是否为二叉排序树。设置一个比所有结点值最小值还小的一个值,与结点从小到大做判断即可。如果最小值比判断的值大,则说明不是二叉排序树;如果最小值比判断的值小,则接着往下做判断,直到树的最后一个结点。如果是二叉排序树,则最小值应该是最左侧的值,只要比这个值小。
int minnum=-32768,flag=1; typedef struct node { int key; struct node *lchild,*rchild; }bitree;void inorder(bitree *bt) { if (bt!=0) { inorder(bt->lchild); if(minnum>bt->key) flag=0; minnum=bt->key; inorder(bt->rchild); } }04
设计一个算法,求出给定的二叉排序树中最小和最大的关键字
算法思想: 在一棵排序二叉树中,最左下结点即为关键字最小的结点,最右下结点即为关键字最大的结点。KeyType MinKey(BiTree *bt){ //求出排序二叉树中最小关键字结点 while(bt->lchild != NULL) bt = bt->lchild; return bt->data; }KeyType MaxKey(BiTree *bt){ //求出排序二叉树中最大关键字结点 while(bt->rchild != NULL) bt = bt->rchild; return bt->data; }
给个“在看”支持一下我

最后
以上就是动人夕阳最近收集整理的关于l2-006 树的遍历 (25分)_这两棵树每年必考,会了至少加6分的全部内容,更多相关l2-006内容请搜索靠谱客的其他文章。








发表评论 取消回复