我是靠谱客的博主 高兴白猫，最近开发中收集的这篇文章主要介绍第二章 数据结构 【完结】单链表[静态]双链表[静态]栈队列单调栈单调队列KMPTrie并查集堆哈希表，觉得挺不错的，现在分享给大家，希望可以做个参考。
概述
栈那节表达式求值，并查集食物链还没做
堆，哈希表不熟，比赛的时候也很少遇到，故没有经常的练习。
目录
- 单链表[静态]
- 双链表[静态]
- 栈
- 队列
- 单调栈
- 单调队列
- KMP
- Trie
- 并查集
- 堆
- 哈希表
单链表[静态]
模板题 AcWing 826. 单链表
y神模板:
// head存储链表头，e[]存储节点的值，ne[]存储节点的next指针，idx表示当前用到了哪个节点
int head, e[N], ne[N], idx;
// 初始化
void init()
{
head = -1;
idx = 0;
}
// 在链表头插入一个数a
void insert(int a)
{
e[idx] = a, ne[idx] = head, head = idx ++ ;
}
// 将头结点删除，需要保证头结点存在
void remove()
{
head = ne[head];
}
需要注意的是: idx是一直递增的
完整的代码:
#include<cstdio>
#include<iostream>
using namespace std;
const int N=1e5+10;
//head 指向头节点的指针
//e[N] 保存该节点的值
//ne[N]保存该节点的下一个节点的地址
//idx 表示目前分配到哪里的指针
int head,idx;
int e[N],ne[N];
void init()//初始化
{
head=-1;
idx=0;
}
void add_to_head(int x)//将x插到头节点
{
ne[idx]=head;
e[idx]=x;
head=idx;
idx++;
}
void add(int k,int x)//将x插入到下标是k的点后面
{
ne[idx]=ne[k];
e[idx]=x;
ne[k]=idx;
idx++;
}
void remove(int k)//将下标是k的点的后面的点删除
{
ne[k]=ne[ne[k]];
}
int main(void)
{
int n; cin>>n;
init();
while(n--)
{
char op; cin>>op;
if(op=='H')
{
int x; cin>>x;
add_to_head(x);
}
if(op=='I')
{
int k,x; cin>>k>>x;
add(k-1,x);
}
if(op=='D')
{
int k; cin>>k;
if(!k) head=ne[head];
remove(k-1);
}
}
for(int i=head;i!=-1;i=ne[i]) cout<<e[i]<<" ";
return 0;
}
双链表[静态]
模板题 AcWing 827. 双链表
双链表的初始状态
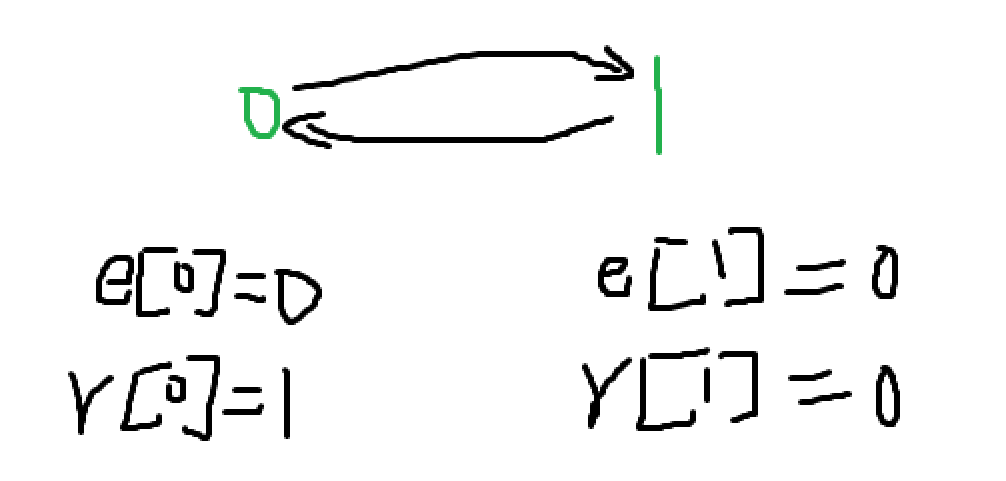
当我们从链表的最左边插入的时候，是从0的右边插入的。
当我们从链表的最右边插入的时候，是从1的左边插入的。
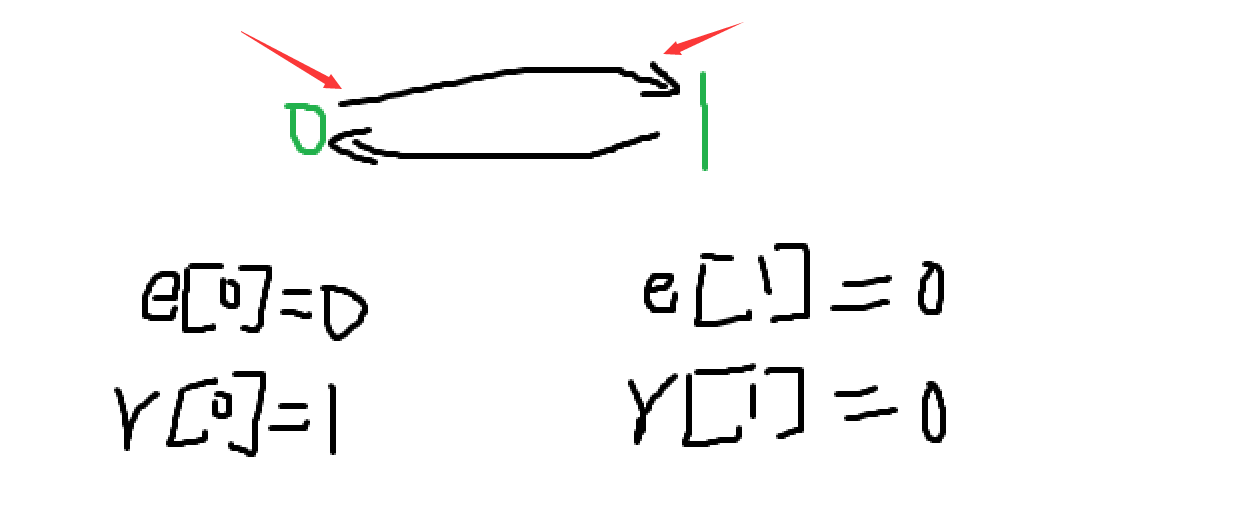
y神模板:
// e[]表示节点的值，l[]表示节点的左指针，r[]表示节点的右指针，idx表示当前用到了哪个节点
int e[N], l[N], r[N], idx;
// 初始化
void init()
{
//0是左端点，1是右端点
r[0] = 1, l[1] = 0;
idx = 2;
}
// 在节点a的右边插入一个数x
void insert(int a, int x)
{
e[idx] = x;
l[idx] = a, r[idx] = r[a];
l[r[a]] = idx, r[a] = idx ++ ;
}
// 删除节点a
void remove(int a)
{
l[r[a]] = l[a];
r[l[a]] = r[a];
}
完整的代码:
#include<cstdio>
#include<iostream>
using namespace std;
const int N=100010;
int m;
int e[N],l[N],r[N],idx;
//在节点a的右边插入一个数
void insert(int a,int x)
{
e[idx]=x;
l[idx]=a,r[idx]=r[a];
l[r[a]]=idx,r[a]=idx++;
}
//删除节点
void remove(int a)
{
l[r[a]]=l[a];
r[l[a]]=r[a];
}
void init()
{
r[0]=1,l[1]=0;
idx=2;
}
int main(void)
{
cin>>m;
init();
while(m--)
{
string op; cin>>op;
int k,x;
if(op=="L")
{
cin>>x;
insert(0,x);
}
if(op=="R")
{
cin>>x;
insert(l[1],x);
}
if(op=="D")
{
cin>>k;
remove(k+1);
}
if(op=="IL")
{
cin>>k>>x;
insert(l[k+1],x);
}
if(op=="IR")
{
cin>>k>>x;
insert(k+1,x);
}
}
for(int i=r[0];i!=1;i=r[i]) cout<<e[i]<<" ";
cout<<endl;
}
栈
模板题 AcWing 828. 模拟栈
3302. 表达式求值 不会
#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>
#include <unordered_map>
using namespace std;
stack<int> num;
stack<char> op;
void eval()
{
auto b = num.top(); num.pop();
auto a = num.top(); num.pop();
auto c = op.top(); op.pop();
int x;
if (c == '+') x = a + b;
else if (c == '-') x = a - b;
else if (c == '*') x = a * b;
else x = a / b;
num.push(x);
}
int main()
{
unordered_map<char, int> pr{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}};
string str;
cin >> str;
for (int i = 0; i < str.size(); i ++ )
{
auto c = str[i];
if (isdigit(c))
{
int x = 0, j = i;
while (j < str.size() && isdigit(str[j]))
x = x * 10 + str[j ++ ] - '0';
i = j - 1;
num.push(x);
}
else if (c == '(') op.push(c);
else if (c == ')')
{
while (op.top() != '(') eval();
op.pop();
}
else
{
while (op.size() && op.top() != '(' && pr[op.top()] >= pr[c]) eval();
op.push(c);
}
}
while (op.size()) eval();
cout << num.top() << endl;
return 0;
}
y神模板:
// tt表示栈顶
int stk[N], tt = 0;
// 向栈顶插入一个数
stk[ ++ tt] = x;
// 从栈顶弹出一个数
tt -- ;
// 栈顶的值
stk[tt];
// 判断栈是否为空
if (tt > 0)
{
}
完整代码:
#include<cstdio>
#include<iostream>
using namespace std;
const int N=1e5+10;
int st[N],tt;
int main(void)
{
int m; cin>>m;
while(m--)
{
string op; cin>>op;
if(op=="push")
{
int x; cin>>x;
st[++tt]=x;
}
if(op=="pop") tt--;
if(op=="query") cout<<st[tt]<<endl;
if(op=="empty")
if(tt>0) cout<<"NO"<<endl;
else cout<<"YES"<<endl;
}
}
队列
模板题 AcWing 829. 模拟队列
普通队列:
1. 普通队列：
// hh 表示队头，tt表示队尾
int q[N], hh = 0, tt = -1;
// 向队尾插入一个数
q[ ++ tt] = x;
// 从队头弹出一个数
hh ++ ;
// 队头的值
q[hh];
// 判断队列是否为空
if (hh <= tt)
{
}
完整代码:
#include<cstdio>
#include<iostream>
using namespace std;
const int N=1e5+10;
int q[N],hh,tt=-1;
int main(void)
{
int m; cin>>m;
while(m--)
{
string op; cin>>op;
if(op=="push")
{
int x; cin>>x;
q[++tt]=x;
}
if(op=="pop") hh++;
if(op=="empty")
{
if(hh<=tt) cout<<"NO"<<endl;
else cout<<"YES"<<endl;
}
if(op=="query") cout<<q[hh]<<endl;
}
return 0;
}
循环队列
// hh 表示队头，tt表示队尾的后一个位置
int q[N], hh = 0, tt = 0;
// 向队尾插入一个数
q[tt ++ ] = x;
if (tt == N) tt = 0;
// 从队头弹出一个数
hh ++ ;
if (hh == N) hh = 0;
// 队头的值
q[hh];
// 判断队列是否为空
if (hh != tt)
{
}
单调栈
关于单调栈的文章
模板题 AcWing 830. 单调栈
y神模板:
常见模型：找出每个数左边离它最近的比它大/小的数
int tt = 0;
for (int i = 1; i <= n; i ++ )
{
while (tt && check(stk[tt], i)) tt -- ;
stk[ ++ tt] = i;
}
完整代码:
#include<cstdio>
#include<iostream>
using namespace std;
const int N=1e5+10;
int st[N],x;
int tt=0;
int main(void)
{
int n; cin>>n;
while(n--)
{
cin>>x;
while(st[tt]>=x) tt--;//栈顶元素大于当前元素，则出栈
if(!tt) cout<<"-1"<<" ";;//栈空，输出-1
if(tt) cout<<st[tt]<<" ";//非空，输出栈顶元素
st[++tt]=x;
}
return 0;
}
单调队列
模板题 AcWing 154. 滑动窗口
y神模板:
常见模型：找出滑动窗口中的最大值/最小值
int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ )
{
while (hh <= tt && check_out(q[hh])) hh ++ ; // 判断队头是否滑出窗口
while (hh <= tt && check(q[tt], i)) tt -- ;
q[ ++ tt] = i;
}
总的代码:
#include<cstdio>
#include<iostream>
using namespace std;
const int N=1e6+10;
int a[N],q[N];
int hh,tt;
int n,k;
int main(void)
{
cin>>n>>k;
for(int i=0;i<n;i++) scanf("%d",&a[i]);
hh=0,tt=-1;
for(int i=0;i<n;i++)//这里的q是一个递增的序列 , 队首元素就是所求的最小值
{
if(i-k+1>q[hh]) hh++;//窗口出界了
while(hh<=tt&&a[i]<=a[q[tt]]) tt--;//不满足单调性
q[++tt]=i;//q保存的是a数组的下标
if(i+1>=k) printf("%d ",a[q[hh]]);
}
cout<<endl;
hh=0,tt=-1;
for(int i=0;i<n;i++)//这里的q是一个递减的序列
{
if(i-k+1>q[hh]) hh++;
while(hh<=tt&&a[i]>a[q[tt]]) tt--;
q[++tt]=i;
if(i+1>=k) printf("%d ",a[q[hh]]);
}
return 0;
}
KMP
模板题 AcWing 831. KMP字符串
y神模板:
// s[]是长文本，p[]是模式串，n是s的长度，m是p的长度
求模式串的Next数组：
for (int i = 2, j = 0; i <= m; i ++ )
{
while (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j ++ ;
ne[i] = j;
}
// 匹配
for (int i = 1, j = 0; i <= n; i ++ )
{
while (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j ++ ;
if (j == m)
{
j = ne[j];
// 匹配成功后的逻辑
}
}
总的代码:
#include<cstdio>
#include<iostream>
using namespace std;
const int N=100010,M=1000010;
int n,m;
int ne[N];
char s[M],p[N];
int main(void)
{
cin>>n>>p+1>>m>>s+1;
//求Next数组：
// s[]是模式串，p[]是模板串, n是s的长度，m是p的长度
// 为什么要从i = 2开始匹配？因为next[1] = 0，已经确定了，所以应该从i = 2开始匹配。
// 注意：next[i]的定义是非平凡的最大后缀等于最大前缀，next[i]必须要小于i
// 对于每一个i开始匹配过程
for (int i = 2, j = 0; i <= n; i ++ )
{
// 如果p[i] != p[j + 1]那么，就跳到ne[j]再进行匹配p[i]与p[j + 1]，直到p[i] == p[j + 1]或j = 0为止
// j一定要大于0，因为j大于0才能跳转到next[j]嘛，ne[0]没有意义
while (j && p[i] != p[j + 1]) j = ne[j];
// 如果一直跳转到 p[i] == p[j + 1]，那么就可以移动j
if (p[i] == p[j + 1])
{
j ++ ;
ne[i] = j;
}
// 否则就说明i点没有最大后缀等于最大前缀
else
{
ne[i] = 0;
}
}
// 匹配
for (int i = 1, j = 0; i <= m; i ++ )
{
while (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j ++ ;
if (j == n)
{
printf("%d ",i-n);
j = ne[j];
// 匹配成功后的逻辑
}
}
return 0;
}
Trie
Trie的概念: 高效地存储和查找字符串集合的数据结构。
835. Trie字符串统计
143. 最大异或对
240. 食物链 未解决
y神的模板:
int son[N][26], cnt[N], idx;
// 0号点既是根节点，又是空节点
// son[][]存储树中每个节点的子节点
// cnt[]存储以每个节点结尾的单词数量
// 插入一个字符串
void insert(char *str)
{
int p = 0;
for (int i = 0; str[i]; i ++ )
{
int u = str[i] - 'a';
if (!son[p][u]) son[p][u] = ++ idx;
p = son[p][u];
}
cnt[p] ++ ;
}
// 查询字符串出现的次数
int query(char *str)
{
int p = 0;
for (int i = 0; str[i]; i ++ )
{
int u = str[i] - 'a';
if (!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
首先要注意的一点就是: N代表的是输入的字符串总长度。
也就是说，这个Trie树的结点个数和是小于等于N的。
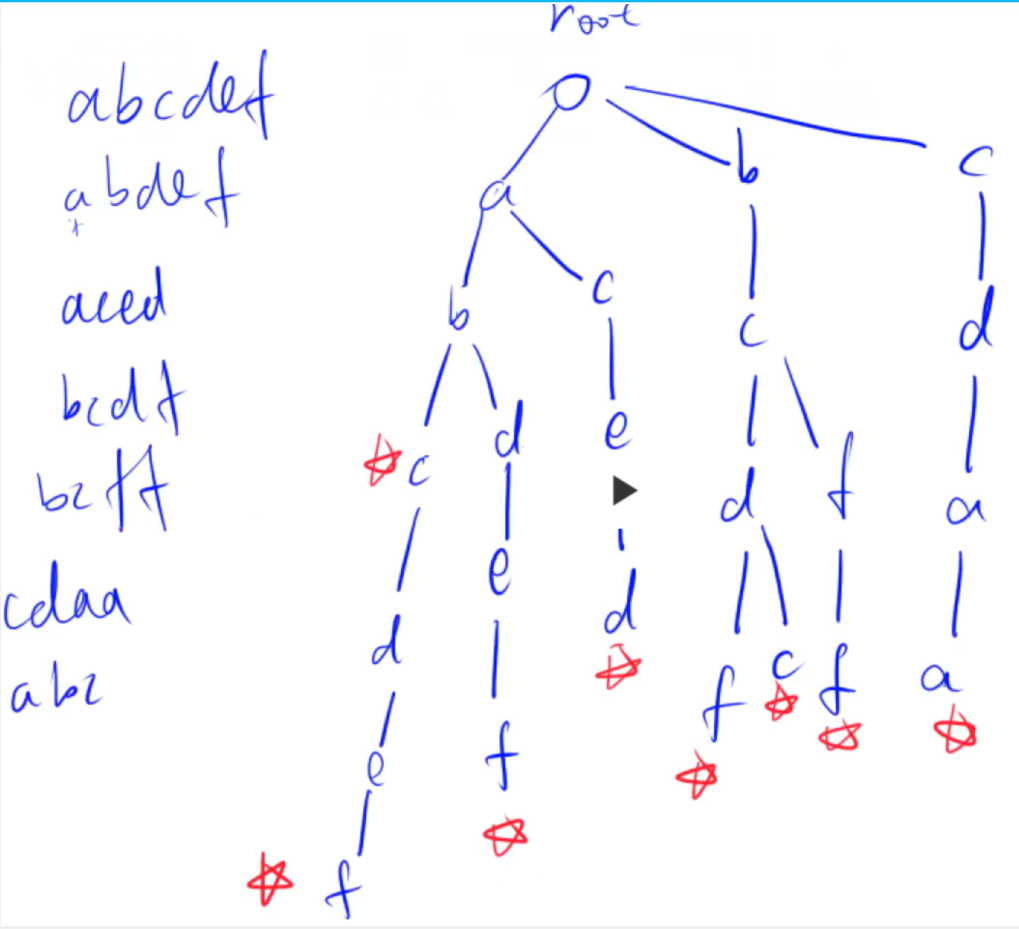
第二点 idx的含义：其实和单链表里的那个含义差不多，如下图我已经用绿笔标出了结点对应的idx的值
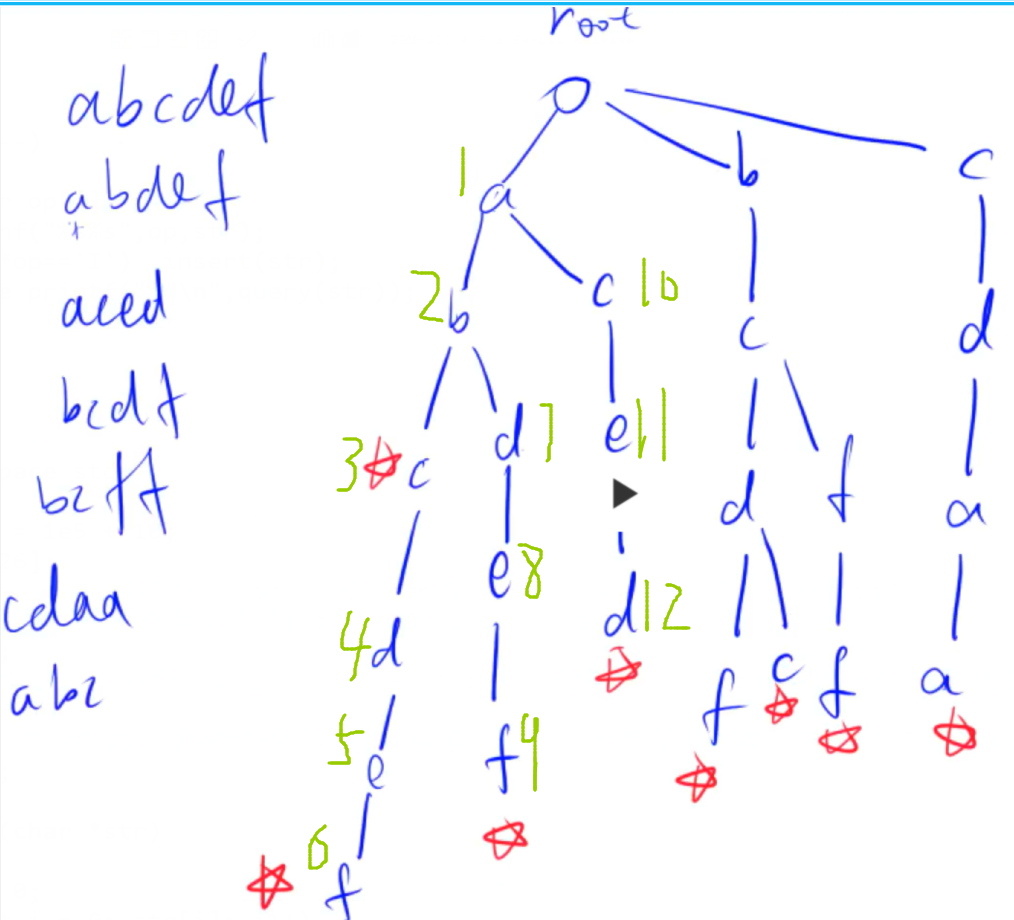
需要注意的一点就是我们的每一个点，对应的idx都是唯一的，这样我们再找儿子的过程中就不会有一对多的情形。
第三点son[N] [26] 的含义
很多小伙伴，不知道这个的含义是啥。其是只要带个案例模拟一边你就懂了。
例: son[0][u] 这个的含义就是根节点它的孩子u结点的下标，跟单链表里的next指针其实是一样的。
不过有区别的一点是我们的单链表它的孩子只有一个，是一条链子。
但是我们的Trie是后面可能有26个孩子(因为英文字母只有26个)，即有26种路径可以选的单链表。
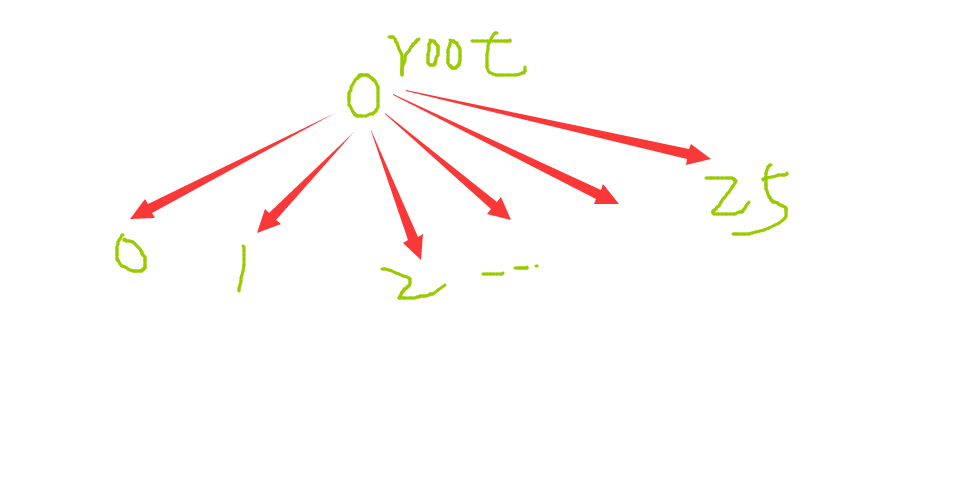
例: abc
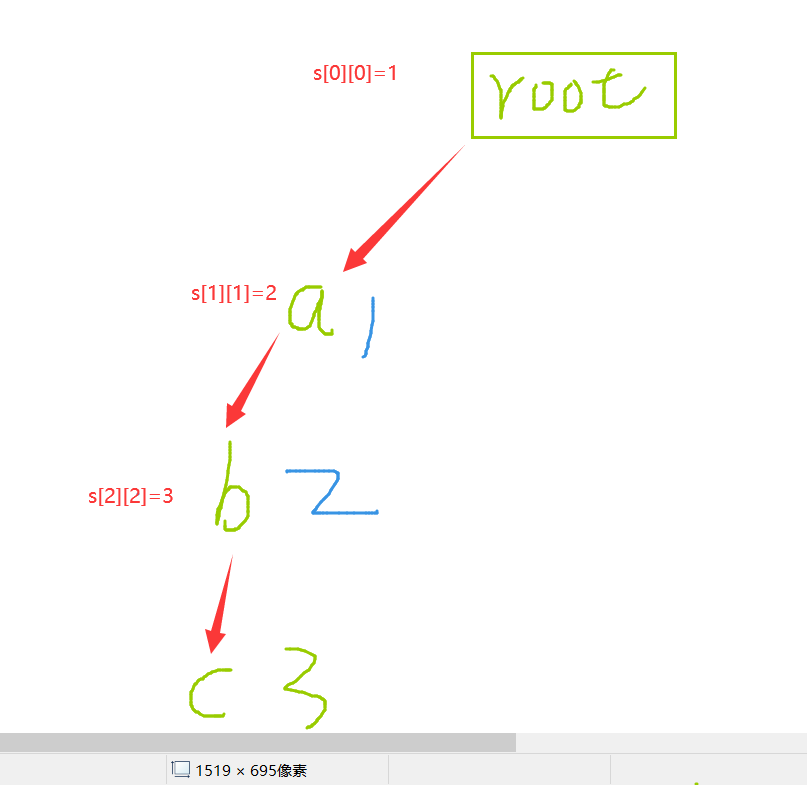
其实只要把字符串的每条路径当成一个单链表，就十分的容易理解了。
最后cnt[p] 的含义
就是该字符串出现的次数。比如上图的: abc 这条字符串单链表已经到头了，那么我们就 cnt[p]++,
p代表的就是c字符所对应的idx,idx我已经说了它和一个字符是唯一对应的，这里的唯一对应不仅是字符对应的关系还有位置(即树的层数)。
因为第1层的" a " 和 第二层的 " a ” 是不同的。
总的代码:
#include<cstdio>
#include<iostream>
using namespace std;
const int N=100010;
int s[N][26],cnt[N],idx;
void insert(string str)
{
int p=0;
for(int i=0;str[i];i++)
{
int u=str[i]-'a';
if(!s[p][u]) s[p][u]=++idx;
p=s[p][u];
}
cnt[p]++;
}
int query(string str)
{
int p=0;
for(int i=0;str[i];i++)
{
int u=str[i]-'a';
if(!s[p][u]) return 0;//没有找到
p=s[p][u];//下一个结点的指针
}
return cnt[p];
}
int main(void)
{
int n; cin>>n;
while(n--)
{
string op,str;cin>>op>>str;
if(op=="I") insert(str);
else cout<<query(str)<<endl;
}
}
还有一点就是我们每次是从根节点开始找的，找到就继续找，没有找到就创建子结点。
并查集
836. 合并集合
837. 连通块中点的数量
y神模板:
(1)朴素并查集：
int p[N]; //存储每个点的祖宗节点
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化，假定节点编号是1~n
for (int i = 1; i <= n; i ++ ) p[i] = i;
// 合并a和b所在的两个集合：
p[find(a)] = find(b);
(2)维护size的并查集：
int p[N], size[N];
//p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化，假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
size[i] = 1;
}
// 合并a和b所在的两个集合：
size[find(b)] += size[find(a)];
p[find(a)] = find(b);
(3)维护到祖宗节点距离的并查集：
int p[N], d[N];
//p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x)
{
int u = find(p[x]);
d[x] += d[p[x]];
p[x] = u;
}
return p[x];
}
// 初始化，假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
d[i] = 0;
}
// 合并a和b所在的两个集合：
p[find(a)] = find(b);
d[find(a)] = distance; // 根据具体问题，初始化find(a)的偏移量
堆
838. 堆排序
839. 模拟堆
y神模板：
// h[N]存储堆中的值, h[1]是堆顶，x的左儿子是2x, 右儿子是2x + 1
// ph[k]存储第k个插入的点在堆中的位置
// hp[k]存储堆中下标是k的点是第几个插入的
int h[N], ph[N], hp[N], size;
// 交换两个点，及其映射关系
void heap_swap(int a, int b)
{
swap(ph[hp[a]],ph[hp[b]]);
swap(hp[a], hp[b]);
swap(h[a], h[b]);
}
void down(int u)
{
int t = u;
if (u * 2 <= size && h[u * 2] < h[t]) t = u * 2;
if (u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
if (u != t)
{
heap_swap(u, t);
down(t);
}
}
void up(int u)
{
while (u / 2 && h[u] < h[u / 2])
{
heap_swap(u, u / 2);
u >>= 1;
}
}
// O(n)建堆
for (int i = n / 2; i; i -- ) down(i);
哈希表
840. 模拟散列表
一般哈希：
(1) 拉链法
int h[N], e[N], ne[N], idx;
// 向哈希表中插入一个数
void insert(int x)
{
int k = (x % N + N) % N;
e[idx] = x;
ne[idx] = h[k];
h[k] = idx ++ ;
}
// 在哈希表中查询某个数是否存在
bool find(int x)
{
int k = (x % N + N) % N;
for (int i = h[k]; i != -1; i = ne[i])
if (e[i] == x)
return true;
return false;
}
(2) 开放寻址法
int h[N];
// 如果x在哈希表中，返回x的下标；如果x不在哈希表中，返回x应该插入的位置
int find(int x)
{
int t = (x % N + N) % N;
while (h[t] != null && h[t] != x)
{
t ++ ;
if (t == N) t = 0;
}
return t;
}
字符串哈希：
841. 字符串哈希
y神模板:
核心思想：将字符串看成P进制数，P的经验值是131或13331，取这两个值的冲突概率低
小技巧：取模的数用2^64，这样直接用unsigned long long存储，溢出的结果就是取模的结果
typedef unsigned long long ULL;
ULL h[N], p[N]; // h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64
// 初始化
p[0] = 1;
for (int i = 1; i <= n; i ++ )
{
h[i] = h[i - 1] * P + str[i];
p[i] = p[i - 1] * P;
}
// 计算子串 str[l ~ r] 的哈希值
ULL get(int l, int r)
{
return h[r] - h[l - 1] * p[r - l + 1];
}
最后
以上就是高兴白猫为你收集整理的第二章 数据结构 【完结】单链表[静态]双链表[静态]栈队列单调栈单调队列KMPTrie并查集堆哈希表的全部内容，希望文章能够帮你解决第二章 数据结构 【完结】单链表[静态]双链表[静态]栈队列单调栈单调队列KMPTrie并查集堆哈希表所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
![第二章 数据结构 【完结】单链表[静态]双链表[静态]栈队列单调栈单调队列KMPTrie并查集堆哈希表](/uploads/reation/bcimg13.png)
发表评论 取消回复