我是靠谱客的博主 内向唇膏，最近开发中收集的这篇文章主要介绍相机运动估计 一、2D - 2D一、不同求解方法的分类 二、2D - 2D 对极几何三、讨论 ，觉得挺不错的，现在分享给大家，希望可以做个参考。
概述
目录
一、不同求解方法的分类
二、2D - 2D 对极几何
1 对极约束
2 本质矩阵
3 单应矩阵
三、讨论
三角测量
一、不同求解方法的分类
假设我们已经有了匹配好的特征点对，然后根据点对估计相机运动，优于相机的原理不同，情况发生了变化：
情况一：当相机为单目时，我们只知道
2D
的像素坐标，因而问题是根据
两组
2D
点
估计运 动。该问题用对极几何
来解决。
情况二：当相机为双目、
RGB-D
时，或者我们通过某种方法得到了距离信息，那问题就是根 据两组
3D
点
估计运动。该问题通常用
ICP
来解决。
情况三：如果我们有
3D
点和它们在相机的投影位置，也能估计相机的运动。该问题通过
PnP 求解。
二、2D - 2D 对极几何
1 对极约束
现在，假设我们从两张图像中，得到了一对配对好的特征点，像图
7-7
里显示的那样。 如果我们有若干对这样的匹配点，
就可以通过这些二维图像点的对应关系，恢复出在两帧 之间摄像机的运动。这里“若干对”具体是多少对呢？我们会在下文介绍。
先来看看两个 图像当中的匹配点有什么几何关系吧。
2 本质矩阵
3 单应矩阵
除了基本矩阵和本质矩阵，我们还有一种称为单应矩阵（
Homography
）
H
的东西，它 描述了两个平面之间的映射关系。
若场景中的特征点都落在同一平面上（比如墙，地面等），则可以通过单应性来进行运动估计。
这种情况在无人机携带的俯视相机，或扫地机携带顶视相机中比较常见。由于之前没提到过单应，我们稍微介绍一下。
单应矩阵通常描述处于共同平面上的一些点，在两张图像之间的变换关系。考虑在图 像 I
1
和
I
2
有一对匹配好的特征点
p
1
和
p
2
。
这些特征点落在某平面上。设这个平面满足 方程：
请注意这里的等号是在非零因子下成立的。我们在实际处理中，通常乘以一个非零因子使得
h
9
= 1
（在它取非零值时）。
然后根据第三行，去掉这个非零因子，于是有：
这种做法把
H
矩阵看成了向量，通过解该向量的线性方程来恢复
H
，又称直接线性 变换法（Direct Linear Transform
）。
与本质矩阵相似，求出单应矩阵以后需要对其进行分 解，才可以得到相应的旋转矩阵 R
和平移向量
t
。
分解的方法包括数值法
[42, 43]
与解析 法 [44]
。与本质矩阵的分解类似，单应矩阵的分解同样会返回四组旋转矩阵与平移向量，并
且同时可以计算出它们分别对应的场景点所在平面的法向量。如果已知成像的地图点的深 度全为正值（即在相机前方），
则又可以排除两组解。最后仅剩两组解，这时需要通过更多 的先验信息进行判断。通常我们可以通过假设已知场景平面的法向量来解决，
如场景平面 与相机平面平行，那么法向量 n
的理论值为
1
T
。 单应性在 SLAM
中具重要意义。当特征点共面，或者相机发生纯旋转的时候，基础矩
阵的自由度下降，这就出现了所谓的退化（degenerate）。现实中的数据总包含一些噪声，这时候如果我们继续使用八点法求解基础矩阵，
基础矩阵多余出来的自由度将会主要由噪声决定。为了能够避免退化现象造成的影响，通常我们会同时估计基础矩阵 F 和单应矩阵
H
，选择重投影误差比较小的那个作为最终的运动估计矩阵。
三、讨论
E
和
F
之差相差了相机内参矩阵。虽然它们在数值 上并不直观，但可以验证它们的数学关系。从 E
,
F
和
H
都可以分解出运动，不过
H
需
要假设特征点位于平面上。对于本实验的数据，这个假设是不好的，所以我们这里主要用
E
来分解运动。
值得一提的是，由于
E
本身具有尺度等价性，它分解得到的
t
,
R
也有一个尺度等价 性。而 R
∈
SO
(3)
自身具有约束，
所以我们认为
t
具有一个
尺度
。换言之，在分解过程 中，对 t
乘以任意非零常数，分解都是成立的。因此，我们通常把
t
进行
归一化
，让它的 长度等于 1
。
尺度不确定性
对
t
长度的归一化，直接导致了
单目视觉的尺度不确定性（
Scale Ambiguity
）
。例 如，程序中输出的 t
第一维约
0.822
。
这个
0.822
究竟是指
0.822
米呢，还是
0.822
厘米 呢，我们是没法确定的。因为对 t
乘以任意比例常数后，对极约束依然是成立的。
换言之， 在单目 SLAM
中，对轨迹和地图同时缩放任意倍数，我们得到的图像依然是一样的。这在 第二讲中就已经给读者介绍过了。
在单目视觉中，我们对两张图像的
t
归一化，相当于
固定了尺度
。虽然我们不知道它 的实际长度为多少，但我们以这时的 t
为单位
1
，
计算相机运动和特征点的
3D
位置。这 被称为单目 SLAM
的
初始化
。在初始化之后，就可以用
3D-2D
来计算相机运动了。初始
化之后的轨迹和地图的单位，就是初始化时固定的尺度。因此，单目
SLAM
有一步不可避 免的初始化
。初始化的两张图像必须有一定程度的平移，
而后的轨迹和地图都将以此步的 平移为单位。 除了对 t
进行归一化之外，另一种方法是令初始化时所有的特征点平均深度为
1
，也
可以固定一个尺度。相比于令
t
长度为
1
的做法，把特征点深度归一化可以控制场景的规 模大小，使计算在数值上更稳定些。不过这并没有理论上的差别。
初始化的纯旋转问题
三角测量
之前两节，我们使用对极几何约束估计了相机运动，也讨论这种方法的局限性。在得 到运动之后，下一步我们需要用相机的运动估计特征点的空间位置。
在单目 SLAM
中，仅 通过单张图像无法获得像素的深度信息，我们需要通过三角测量（
Triangulation
）（或三 角化）的方法来估计地图点的深度。
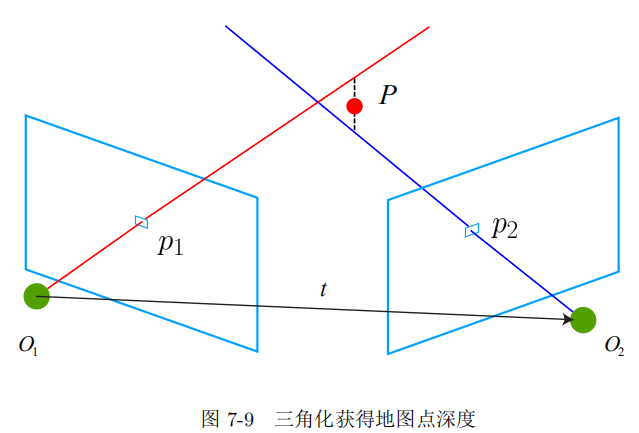
三角测量是指，通过在两处观察同一个点的夹角，确定该点的距离。三角测量最早由 高斯提出并应用于测量学中，它在天文学、地理学的测量中都有应用。例如，我们可以通
过不同季节观察到星星的角度，估计它离我们的距离。在
SLAM
中，我们主要用三角化来 估计像素点的距离。
最后
以上就是内向唇膏为你收集整理的相机运动估计 一、2D - 2D一、不同求解方法的分类 二、2D - 2D 对极几何三、讨论 的全部内容，希望文章能够帮你解决相机运动估计 一、2D - 2D一、不同求解方法的分类 二、2D - 2D 对极几何三、讨论 所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复