机器学习错题集(1)

• 生成模型与判别模型的区别：

  • 在机器学习中，对于有监督学习可以将其分为两类模型：判别式模型和生成式模型。简单地说，判别式模型是针对条件分布建模，而生成式模型则针对联合分布进行建模。已知输入变量x：

    • 生成模型（generative model）通过对观测值和标注数据计算联合概率分布P(x,y)来达到判定估算y的目的。常见的生成模型有朴素贝叶斯（Naive Bayes）, 隐马尔科夫模型（HMM）,贝叶斯网络（Bayesian Networks）和隐含狄利克雷分布（Latent Dirichlet Allocation）。生成模型：$关注数据是如何生成的$。

      • 学习时先得到P(x,y)，继而得到 P(y∣x)。预测时应用最大后验概率法（MAP）得到预测类别 y。生成式模型比判别式模型计算量更大。为了使生成的分布函数与真实世界中的分布函数尽可能接近，需要大量的数据来生成模型。

      • 生成模型： 源头导向。尝试去找到底这个数据是怎么产生的，然后再对一个信号进行分类。基于你学习到的生成假设，判断哪个类别最有可能产生这个信号，这个样本就属于那个类别。

      • 总结：生成式模型主要通过学习样本，形成多个Y分布，然后计算联合概率P(X,Y)，根据P(X,Y)的值预测新的样本属于哪个类。对于二分类问题，如果P(X,Y1)>P(X,Y2)，则新样本X判定为Y1。

    • 判别模型(discriminative model)通过求解条件概率分布P(y|x)或者直接计算y的值来预测y。常见的判别模型有线性回归（Linear Regression）,逻辑回归（Logistic Regression）,支持向量机（SVM）, 传统神经网络（Traditional Neural Networks）,线性判别分析（Linear Discriminative Analysis），条件随机场（Conditional Random Field）。判别模型： $关注类别之间的差别$。

      • 直接学习得到P(y∣x)，利用MAP得到y。或者直接学得一个映射函数 y=f(x)。

      • 判别模型： 结果导向。并不关心样本数据是怎么生成的，它只关心样本之间的差别，然后用差别来简单对给定的一个样本进行分类。

• 中文分词方法：

  • 中文分词的基本方法可以分为基于语法规则的方法、基于词典的方法和基于统计的方法。

  • 基于语法规则的分词法基本思想是在分词的同时进行句法、语义分析, 利用句法信息和语义信息来进行词性标注, 以解决分词歧义现象。因为现有的语法知识、句法规则十分笼统、复杂, 基于语法和规则的分词法所能达到的精确度远远还不能令人满意, 目前这种分词系统应用较少。

  • 在基于词典的方法中，可以进一步分为最大匹配法，最大概率法，最短路径法等。最大匹配法指的是按照一定顺序选取字符串中的若干个字当做一个词，去词典中查找。根据扫描方式可细分为：正向最大匹配，反向最大匹配，双向最大匹配，最小切分。最大概率法指的是一个待切分的汉字串可能包含多种分词结果，将其中概率最大的那个作为该字串的分词结果。最短路径法指的是在词图上选择一条词数最少的路径。

  • 基于统计的分词法的基本原理是根据字符串在语料库中出现的统计频率来决定其是否构成词。词是字的组合，相邻的字同时出现的次数越多, 就越有可能构成一个词。因此字与字相邻共现的频率或概率能够较好的反映它们成为词的可信度。常用的方法有HMM（隐马尔科夫模型），MAXENT（最大熵模型），MEMM（最大熵隐马尔科夫模型），CRF（条件随机场）。

• 分类器评价指标：

  • 对于分类器，主要的评价指标有precision，recall，F-score，以及ROC曲线等。

  • 在二分类问题中，我们主要关注的是测试集的正样本能否正确分类。当样本不均衡时，比如样本中负样本数量远远多于正样本，此时如果负样本能够全部正确分类，而正样本只能部分正确分类，那么(TP+TN)可以得到很高的值，也就是Accuracy是个较大的值，但是正样本并没有取得良好的分类效果。

• I3D算法：

  • ID3算法（IterativeDichotomiser3，迭代二叉树3代）是一个由RossQuinlan发明的用于决策树的算法。可以归纳为以下几点： 使用所有没有使用的属性并计算与之相关的样本熵值选取其中熵值最小的属性 生成包含该属性的节点 D3算法对数据的要求：

    • 1)所有属性必须为离散量；

    • 2)所有的训练例的所有属性必须有一个明确的值；

    • 3)相同的因素必须得到相同的结论且训练例必须唯一。

• 过拟合问题：

  • 机器学习中发生过拟合的主要原因有：

    • （1）使用过于复杂的模型；

    • （2）数据噪声较大；

    • （3）训练数据少。

  • 对应的降低过拟合的方法有：

    • （1）简化模型假设，或者使用惩罚项限制模型复杂度；

    • （2）进行数据清洗，减少噪声；

    • （3）收集更多训练数据。

• bagging和boosting的区别：Understanding the Bias-Variance Tradeoff (fortmann-roe.com)

  • 集成学习是指将若干弱分类器组合之后产生一个强分类器。弱分类器（weak learner）指那些分类准确率只稍好于随机猜测的分类器（error rate < 50%）。如今集成学习有两个流派，一种是bagging流派，它的特点是各个弱学习器之间没有依赖关系，可以并行拟合，随机森林算法就属于bagging派系；另一个是boosting派系，它的特点是各个弱学习器之间有依赖关系，Adaboost算法就属于boosting派系。在实现集成学习算法时，很重要的一个核心就是如何实现数据的多样性，从而实现弱分类器的多样性

  • 在学习总结Bagging和Boosting方法之前，有一个预备知识需要学习：Bias(偏差) & Variance（方差），Bias 和 Variance 分别代表 准 和 确 两个概念。

  • 

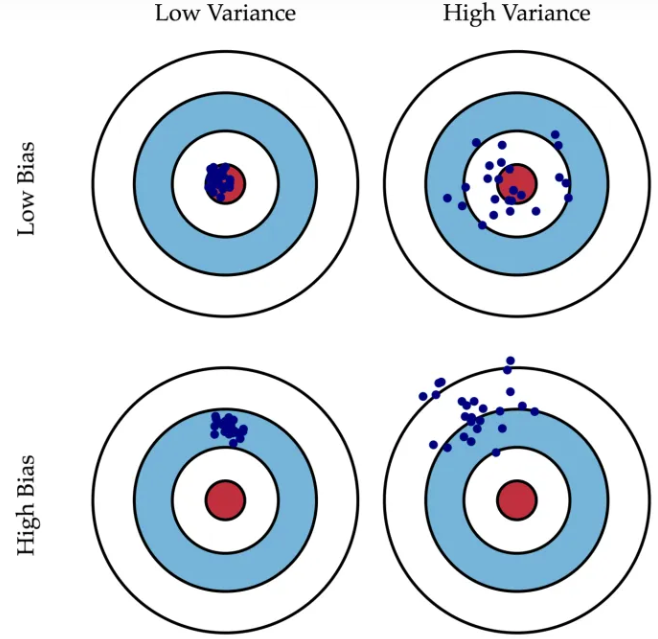
  • Bagging (bootstrap aggregating)

    • Bagging是Bootstrap aggregating的缩写。中文意思是自助聚合。而Bootstrap本身是一种有放回的抽样方法（可能抽到重复的样本）。

      • 从原始样本集中随机采样。每轮从原始样本集中有放回的选取n个训练样本（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中）。共进行k轮抽取，得到k个训练集。（bootstrap的过程，由于是有放回抽样，所以k个训练集之间相互独立）

      • 每次使用一份训练集训练一个模型，k 个训练集共得到 k 个基模型。（注：这里并没有具体的分类算法或回归方法，我们可以根据具体问题采用不同的分类或回归方法，如决策树、感知器等）

      • 利用这k个基模型对测试集进行预测，将k个预测结果进行聚合。(aggregating的过程)

    • 分类问题：将上步得到的k个模型采用投票的方式得到分类结果

    • 回归问题：计算上述模型的均值作为最后的结果。（所有模型的重要性相同）

  • Bagging算法特点：

    • 可并行的集成方法。每个基模型可以分别、独立、互不影响地生成。

    • 主要降低 Variance，对 Bias 无明显作用。因此，适用于 High Variance & Low Bias 的模型。

  • Boosting：核心思想是将多个弱分类器组装成一个强分类器 。关于Boosting的两个核心问题：

    • 在每一轮如何改变训练数据的权值或概率分布？通过提高那些在前一轮被弱分类器分错样例的权值，减小前一轮分对样例的权值，来使得分类器对误分的数据有较好的效果。有传递接力的思想。

    • 通过什么方式来组合弱分类器？通过加法模型将弱分类器进行线性组合，比如AdaBoost通过加权多数表决的方式，即增大错误率小的分类器的权值，同时减小错误率较大的分类器的权值。

  • Boosting算法特点：

    • 序贯式集成方法（Sequential Ensemble）。每轮迭代生成的基模型，主要提升前一代基模型表现不好的地方。

    • 不断迭代弱分类器，从而降低 Bias。因此，适用于 Low Variance & High Bias 的模型。如AdaBoost、GBDT、XGBoost等。

  • Bagging，Boosting二者之间的区别

    • 样本选择：

      • Bagging：训练集是在原始集中有放回选取的，从原始集中选出的各轮训练集之间是独立的。

      • Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。

    • 样例权重：

      • Bagging：使用均匀取样，每个样例的权重相等

      • Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大。

    • 预测函数：

      • Bagging：所有预测函数的权重相等。

      • Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重。

    • 并行计算：

      • Bagging：各个预测函数可以并行生成

      • Boosting：各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果。

  • 这两种方法都是把若干个分类器整合为一个分类器的方法，只是整合的方式不一样，最终得到不一样的效果，将不同的分类算法套入到此类算法框架中一定程度上会提高了原单一分类器的分类效果，但是也增大了计算量。

  • 使用单一决策树对比bagging方法（使用葡萄酒数据集进行建模）

  • import numpy as np
    from matplotlib import pyplot as plt
    import pandas as pd
    df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data',header=None)
    df_wine.columns = ['Class label', 'Alcohol','Malic acid', 'Ash','Alcalinity of ash','Magnesium', 'Total phenols',
                       'Flavanoids', 'Nonflavanoid phenols','Proanthocyanins','Color intensity', 'Hue','OD280/OD315 of diluted wines','Proli i4
    print(df_wine['Class label'].vaunts()
    '''
    2    71
    1    59
    3    48
    Name: Class label, dtype:lue_counts())
    '''
    

  • 有三个类别的葡萄酒，每个类别分别有59，71，48条数据。

  • 数据预处理，问题简单化，只选用两类数据进行二分类：

  • df_wine = df_wine[df_wine['Class label'] != 3]  # drop 1 class
    y = df_wine['Class label'].values
    X = df_wine[['Alcohol','OD280/OD315 of diluted wines']].values
    from sklearn.model_selection import train_test_split  # 切分训练集与测试集
    from sklearn.preprocessing import LabelEncoder   # 标签化分类变量
    le = LabelEncoder()
    y = le.fit_transform(y)  #吧y值改为0和1 ，原来是2和3
    X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=1,stratify=y)  #2、8分
    

• 使用单一决策树进行分类

• ## 我们使用单一决策树分类：
  from sklearn.tree import DecisionTreeClassifier
  tree = DecisionTreeClassifier(criterion='entropy',random_state=1,max_depth=None)   #选择决策树为基本分类器
  from sklearn.metrics import accuracy_score  #计算准确率
  tree = tree.fit(X_train,y_train)
  y_train_pred = tree.predict(X_train)
  y_test_pred = tree.predict(X_test)
  tree_train = accuracy_score(y_train,y_train_pred)  #训练集准确率
  tree_test = accuracy_score(y_test,y_test_pred)  #测试集准确率
  print('Decision tree train/test accuracies %.3f/%.3f' % (tree_train,tree_test))
  

• Decision tree train/test accuracies 1.000/0.846

• ## 我们使用BaggingClassifier分类：
  from sklearn.ensemble import BaggingClassifier
  tree = DecisionTreeClassifier(criterion='entropy',random_state=1,max_depth=None)   #选择决策树为基本分类器
  bag = BaggingClassifier(base_estimator=tree,n_estimators=500,max_samples=1.0,max_features=1.0,bootstrap=True,
                          bootstrap_features=False,n_jobs=1,random_state=1)
  from sklearn.metrics import accuracy_score
  bag = bag.fit(X_train,y_train)
  y_train_pred = bag.predict(X_train)
  y_test_pred = bag.predict(X_test)
  bag_train = accuracy_score(y_train,y_train_pred)
  bag_test = accuracy_score(y_test,y_test_pred)
  print('Bagging train/test accuracies %.3f/%.3f' % (bag_train,bag_test))
  

• Bagging train/test accuracies 1.000/0.885

• 可视化二分类边界

  • 

  • 从结果图看起来，三个节点深度的决策树分段线性决策边界在Bagging集成中看起来更加平滑

• 随机事件 X 所包含的信息量与其发生的概率有关。发生的概率越小，其信息量就越大；反之，必定发生的事件（如太阳东升西落），其信息量为 0。 信息量公式：I(X) = −logp(X) ，其中 I 是 information 的缩写。

  • 信息量公式的单位： log 以2为底，记作lb，单位比特（bit） log 以e为底，记作ln，单位奈特（nat） log 以10为底，记作lg，单位哈脱来（hat）

  • 信息熵：随机变量 X 不确定性的度量，是对 X 所有可能值产生的信息量的期望。

    • $$H(X)=-\sum _{i=1}^{n}p(x_i)logp(x_i)$$

    • 由公式可知：信息熵只与随机变量X的概率分布 p(x) 有关。

  • 条件熵：表示在已知随机变量 X 的条件下随机变量 Y 的不确定性。

  • $$H(Y|X)=-\sum _{x}p(x)\sum _{y}p(y|x)logp(y|x)$$

  • 已知P(x=-1)=1/4，P(x=1)=3/4，P(y=-1|x=-1)=4/5，P(y=0|x=-1)=1/5，P(y=1|x=1)=3/4，P(y=0|x=1)=1/4，求条件熵H(Y|X)，则：

  • $$H(Y|X)=-[\frac{1}{4}\ast (\frac{4}{5}\ast lo{g}_2\frac{4}{5}+\frac{1}{5}\ast lo{g}_2\frac{1}{5})+\frac{3}{4}\ast (\frac{3}{4}\ast lo{g}_2\frac{3}{4}+\frac{1}{4}\ast lo{g}_2\frac{1}{4})]$$

• 线性判别分析（Linear Discriminant Analysis）简称 LDA，在二分类问题上最早由Fisher提出，故又称Fisher判别分析。 在二分类问题上，Fisher判别分析的基本思想是：在训练时，将训练样本投影到某条直线上，这条直线可以使得同类型样本的投影点尽可能接近，而异类型样本的投影点尽可能远离。在预测时，将待预测数据投影到训练时学习到的直线上，根据投影点的位置来判断所属于的类别。如图所示：

  • 

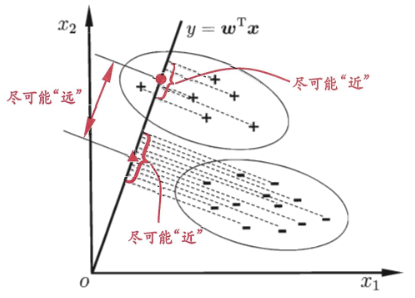
  • Fisher判别分析可以将二维特征向量投影到一维空间。推广到多分类任务中，Fisher判别分析可以将 M 维特征向量投影到 M-1 维空间，即：Fisher判别函数的求解过程是将M维特征矢量投影到M-1维空间中进行求解。 补充：Fisher判别分析（即LDA）经常被视为一种经典的有监督降维技术。

• “不能求解线性不可分情况下的分类问题” 即：“不能求解非线性分类问题”，感知器算法属于线性分类模型，故不能求解非线性分类问题。

• 朴素贝叶斯的条件就是每个变量相互独立。在贝叶斯理论系统中，都有一个重要的条件独立性假设：假设所有特征之间相互独立，这样才能将联合概率拆分。 此外，若高度相关的特征在模型中引入两次, 这样增加了这一特征的重要性, 则它的性能因数据包含高度相关的特征而下降。正确做法是评估特征的相关矩阵，并移除那些高度相关的特征。

• K-L变换与PCA变换是不同的概念，PCA的变换矩阵是协方差矩阵，K-L变换的变换矩阵可以有很多种（二阶矩阵、协方差矩阵、总类内离散度矩阵等等）。当K-L变换矩阵为协方差矩阵时，等同于PCA。

• 聚类的任务只是把数据按照相似性原则进行划分，不存在分类问题中由于训练集样本存在噪声数据，从而影响分类结果的情况。 在类别已知的情况下，直接按照样本的类别标签进行聚类就可以了，用不到复杂的聚类算法，所以也就不存在影响聚类算法结果这么一说了。分类准则是指选取什么特征将该特征相似的数据聚为一类，这个会直接影响到样本聚类的结果；特征选取、相似性测度也是影响聚类算法结果的因素。

• 欧氏距离是在N维空间中两个点的真实距离；马氏距离表示数据的协方差距离。 而欧式距离的特征是：平移不变性、旋转不变性。 马式距离的特征则是：平移不变性、旋转不变性、尺度不变性、不受量纲影响、考虑了模式分布。 所以马式距离相比欧式距离的优点：尺度不变性、不受量纲影响、考虑了模式分布。换句话说，不属于马式距离较之于欧式距离的优点是：平移不变性、旋转不变性。

• 传统的Ｋ均值算法随机选取初始聚类中心，往往会造成聚类结果陷入局部最优解，故改进初始类中心的选取方法可以提升Ｋ均值算法的聚类效果。样本的输入顺序会影响到初始类中心的选取结果。 模式相似性测度是指数据相似性的测量标准，比如通过计算两个数据的欧式距离大小，来判定他们的相似程度，进而确定他们是否属于同类。欧氏距离越小，说明数据越接近，相似性越大。此外，相似性测度还有马氏距离、余弦相似度等，不同的测度会影响到K-均值算法聚类的结果，这和应聘面试是一个道理，不同的用人单位选用不同的标准，同样的你去应聘成功的概率也会不同。 聚类准则：相似的数据被聚为一类。这个准则是不会变的，故不会对Ｋ均值算法产生影响。

• 在贝叶斯决策中，对于先验概率未知时可以使用聂曼-皮尔逊决策(N-P决策)来计算决策面。最小最大损失规则主要是解决在使用最小损失规则时先验概率未知或难以计算的问题的；最小误判概率准则就是判断p(w1|x)和p(w2|x)哪个大，x为特征向量，w1和w2为两分类，根据贝叶斯公式，需要用到先验知识。

• 线性分类器有三大类：感知器准则函数、SVM、Fisher准则，而贝叶斯分类器不是线性分类器。

  • 感知准则函数 ：准则函数以使错分类样本到分界面距离之和最小为原则。其优点是通过错分类样本提供的信息对分类器函数进行修正，这种准则是人工神经元网络多层感知器的基础。

  • 支持向量机 ：基本思想是在两类线性可分条件下，所设计的分类器界面使两类之间的间隔为最大，它的基本出发点是使期望泛化风险尽可能小。（使用核函数可解决非线性问题）

  • Fisher 准则 ：更广泛的称呼是线性判别分析（LDA），将所有样本投影到一条远点出发的直线，使得同类样本距离尽可能小，不同类样本距离尽可能大，具体为最大化“广义瑞利商”。 根据两类样本一般类内密集，类间分离的特点，寻找线性分类器最佳的法线向量方向，使两类样本在该方向上的投影满足类内尽可能密集，类间尽可能分开。这种度量通过类内离散矩阵 Sw 和类间离散矩阵 Sb 实现。

• Logistic回归是一种十分常见的分类模型，是的严格来说这是一个分类模型，之所以叫做回归也是由于历史原因。不同于线性回归中对于参数的推导，我们在这里运用的方式不再是最小二乘法，而是极大似然估计。

• 支持向量机SVM，考虑加入正则化项的原因：想象一个完美的数据集，y>1是正类，y<-1是负类，决策面y=0，加入一个y=-30的正类噪声样本，那么决策面将会变“歪”很多，分类间隔变小，泛化能力减小。加入正则项之后，对噪声样本的容错能力增强，前面提到的例子里面，决策面就会没那么“歪”了，使得分类间隔变大，提高了泛化能力。

• EM算法： 只有观测序列，无状态序列时来学习模型参数，即Baum-Welch算法；维特比算法： 用动态规划解决HMM的预测问题，不是参数估计；前向后向算法：用来算概率；极大似然估计：即观测序列和相应的状态序列都存在时的监督学习算法，用来估计参数 注意的是在给定观测序列和对应的状态序列估计模型参数，可以利用极大似然发估计。如果给定观测序列，没有对应的状态序列，才用EM，将状态序列看不不可测的隐数据。

• L1范数是向量中各个元素的绝对值之和，又叫稀疏规则算子。L1正则化通过向代价函数中添加权重向量的L1范数（即正则化项），使得优化后的模型中无用特征对应的权值变为0，相当于减少了特征维数，实现了特征的自动选择，所以LR中加入L1范数可以进行特征选择、解决维度灾难问题、加快计算速度；

• L2范数是向量中各个元素平方和的1/2次方。L2正则化通过向代价函数中添加权重向量的L2范数，使得优化后的模型中所有的权值w尽可能趋于0但不为0，通过L2范数，可以实现对模型空间的限制，从而在一定程度上避免了过拟合； 过拟合的时候，拟合函数需要顾忌每一个点，最终形成的拟合函数波动很大， 在某些小区间里，函数值的变化很大，也就是w非常大。所以LR中加入L2范数可以在一定程度上防止过拟合； 在LR中同时加入L1和L2范数不会产生结果更准确的效果。

• L1正则化/Lasso L1正则化将系数w的l1范数作为惩罚项加到损失函数上，由于正则项非零，这就迫使那些弱的特征所对应的系数变成0。因此L1正则化往往会使学到的模型很稀疏（系数w经常为0），这个特性使得L1正则化成为一种很好的特征选择方法。

• L2正则化/Ridge regression L2正则化将系数向量的L2范数添加到了损失函数中。由于L2惩罚项中系数是二次方的，这使得L2和L1有着诸多差异，最明显的一点就是，L2正则化会让系数的取值变得平均。 对于关联特征，这意味着他们能够获得更相近的对应系数。还是以Y=X1+X2为例，假设X1和X2具有很强的关联，如果用L1正则化，不论学到的模型是Y=X1+X2还是Y=2X1，惩罚都是一样的，都是2alpha。但是对于L2来说，第一个模型的惩罚项是2alpha，但第二个模型的是4*alpha。可以看出，系数之和为常数时，各系数相等时惩罚是最小的，所以才有了L2会让各个系数趋于相同的特点。 可以看出，L2正则化对于特征选择来说一种稳定的模型，不像L1正则化那样，系数会因为细微的数据变化而波动。所以L2正则化和L1正则化提供的价值是不同的，L2正则化对于特征理解来说更加有用：表示能力强的特征对应的系数是非零。 因此，一句话总结就是：L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。Lasso在特征选择时候非常有用，而Ridge就只是一种规则化而已。

• 隐马尔科夫模型有三个基本问题：

• 1 概率计算问题：给定模型和观测序列，计算在模型下观测序列出现的概率。

• 2 学习问题：已知观测序列，估计模型中的参数，使得在该模型下观测序列概率最大，即用极大似然估计的方法估计参数。

• 3 预测问题：也称解码问题，已知模型和观测序列，给定观测序列，求最可能的对应的状态序列。

• 解决隐马尔科夫模型三个基本问题的算法：

  • 概率计算算法：前向算法、后向算法

  • 学习算法：Baum-Welch算法

  • 预测算法：近似算法、维特比算法

• 评估问题就是概率计算问题，相应的算法是前向算法和后向算法；解码问题就是预测问题，相应的算法是维特比算法，学习问题相应的算法是Baum-Welch算法，

• 一般情况下，越复杂的系统，过拟合的可能性就越高，一般模型相对简单的话泛化能力会更好一点。一般认为，增加隐层数可以降低网络误差（也有文献认为不一定能有效降低），提高精度，但也使网络复杂化，从而增加了网络的训练时间和出现“过拟合”的倾向， svm高斯核函数比线性核函数模型更复杂，容易过拟合 .径向基(RBF)核函数/高斯核函数的说明,这个核函数可以将原始空间映射到无穷维空间。对于参数 ，如果选的很大，高次特征上的权重实际上衰减得非常快，实际上（数值上近似一下）相当于一个低维的子空间；反过来，如果选得很小，则可以将任意的数据映射为线性可分——当然，这并不一定是好事，因为随之而来的可能是非常严重的过拟合问题。不过，总的来说，通过调整参数 ，高斯核实际上具有相当高的灵活性，也是 使用最广泛的核函数之一。

• AR模型是一种线性预测，即已知N个数据，可由模型推出第N点前面或后面的数据（设推出P点），所以其本质类似于插值。

• MA模型(moving average model)滑动平均模型，其中使用趋势移动平均法建立直线趋势的预测模型。

• ARMA模型(auto regressive moving average model)自回归滑动平均模型，模型参量法高分辨率谱分析方法之一。这种方法是研究平稳随机过程有理谱的典型方法。它比AR模型法与MA模型法有较精确的谱估计及较优良的谱分辨率性能，但其参数估算比较繁琐。

• GARCH模型称为广义ARCH模型，是ARCH模型的拓展，由Bollerslev(1986)发展起来的。它是ARCH模型的推广。GARCH(p,0)模型，相当于ARCH§模型。GARCH模型是一个专门针对金融数据所量体订做的回归模型，除去和普通回归模型相同的之处，GARCH对误差的方差进行了进一步的建模。特别适用于波动性的分析和预测，这样的分析对投资者的决策能起到非常重要的指导性作用，其意义很多时候超过了对数值本身的分析和预测。

• PCA 提取的是数据分布方差比较大的方向，隐藏层可以提取有预测能力的特征

• CNN卷积核卷积计算时可以重复用。 RNN序列的每个时间步的参数都是共享的。

• batch normalization 就是对数据做批规范化，使得数据满足均值为0,方差为1的正太分布。其主要作用是缓解DNN训练中的梯度消失/爆炸现象，加快模型的训练速度。 但是注意是对数据做批规范化，不是对权重。 BN的优点：

  • ①极大提升了训练速度，收敛过程大大加快；

  • ②增加了分类效果，一种解释是这是类似于Dropout的一种防止过拟合的正则化表达方式，所以不用Dropout或正则化也能达到相当的效果；

  • ③简化了调参过程，对于初始化参数权重不太敏感，允许使用较大的学习率

• 传统Ｋ均值算法随机选取初始聚类中心，往往会造成聚类结果陷入局部最优解，改进初始类中心的选取方法可以提升Ｋ均值算法的聚类效果，获得全局最优解。

• 对数损失, 即对数似然损失(Log-likelihood Loss), 也称逻辑斯谛回归损失(Logistic Loss)或交叉熵损失(cross-entropy Loss), 是在概率估计上定义的.它常用于(multi-nominal, 多项)逻辑斯谛回归和神经网络,以及一些期望极大算法的变体. 可用于评估分类器的概率输出。 对数损失通过惩罚错误的分类,实现对分类器的准确度(Accuracy)的量化. 最小化对数损失基本等价于最大化分类器的准确度.为了计算对数损失, 分类器必须提供对输入的所属的每个类别的概率值, 不只是最可能的类别.

• Pearson相关系数只能衡量线性相关性，但无法衡量非线性关系。如y=x^2，x和y有很强的非线性关系。

• 常采用特征选择方法。常见的六种特征选择方法：

  • 1）DF(Document Frequency) 文档频率 DF:统计特征词出现的文档数量，用来衡量某个特征词的重要性

  • 2）MI(Mutual Information) 互信息法 互信息法用于衡量特征词与文档类别直接的信息量。 如果某个特征词的频率很低，那么互信息得分就会很大，因此互信息法倾向"低频"的特征词。 相对的词频很高的词，得分就会变低，如果这词携带了很高的信息量，互信息法就会变得低效。

  • 3）(Information Gain) 信息增益法 通过某个特征词的缺失与存在的两种情况下，语料中前后信息的增加，衡量某个特征词的重要性。

  • 4）CHI(Chi-square) 卡方检验法 利用了统计学中的"假设检验"的基本思想：首先假设特征词与类别直接是不相关的 如果利用CHI分布计算出的检验值偏离阈值越大，那么更有信心否定原假设，接受原假设的备则假设：特征词与类别有着很高的关联度。

  • 5）WLLR(Weighted Log Likelihood Ration)加权对数似然

  • 6）WFO（Weighted Frequency and Odds）加权频率和可能性

• 主成分分析（PCA）通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维； 线性鉴别法（LDA）通过降维找到一个类内距离最小、类间距离最大的空间实现分类； 稀疏自编码（SparseAutoEncoder）就是用少于输入层神经元数量的隐含层神经元去学习表征输入层的特征，相当于把输入层的特征压缩了，所以是特征降维； 在PCA算法中用到了SVD，类似于PCA降维； 至于最小二乘法是用来回归的，不能用于特征降维。

• LASSO通过参数缩减达到降维的目的； 主成分分析法（PCA）通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维； 线性鉴别法（LDA）通过降维找到一个类内距离最小、类间距离最大的空间实现分类； 小波分析有一些变换的操作降低其他干扰，可以看做是降维； 拉普拉斯特征映射将处于流形上的数据，在尽量保留原数据间相似度的情况下，映射到低维下表示，实现降维； 聚类分析不能用来对高维数据进行降维。

• 自回归滑动平均模型(ARMA) 其建模思想可概括为：逐渐增加模型的阶数，拟合较高阶模型，直到再增加模型的阶数而剩余残差方差不再显著减小为止。

• 相对强弱指数 (RSI, Relative Strength Index) 是通过比较一段时期内的平均收盘涨数和平均收盘跌数来分析市场买沽盘的意向和实力 , 从而作出未来市场的走势 .

• 移动平均聚散指标 (MACD, Moving Average Convergence Divergence), 是根据均线的构造原理 , 对股票价格的收盘价进行平滑处理 , 求出算术平均值以后再进行计算 , 是一种趋向类指标

• 随机指标 (KDJ) 一般是根据统计学的原理 , 通过一个特定的周期 ( 常为 9 日 ,9 周等 ) 内出现过的最高价 , 最低价及最后一个计算周期的收盘价及这三者之间的比例关系 , 来计算最后一个计算周期的未成熟随机值 RSV, 然后根据平滑移动平均线的方法来计算 K 值 , D 值与 J 值 , 并绘成曲线图来研判股票走势 .

• SVM核函数包括线性核函数、多项式核函数、径向基核函数、高斯核函数、幂指数核函数、拉普拉斯核函数、ANOVA核函数、二次有理核函数、多元二次核函数、逆多元二次核函数以及Sigmoid核函数。 核函数的定义并不困难，根据泛函的有关理论，只要一种函数 K ( x i , x j ) 满足Mercer条件，它就对应某一变换空间的内积．对于判断哪些函数是核函数到目前为止也取得了重要的突破，得到Mercer定理和以下常用的核函数类型：

  • (1)线性核函数 K ( x , x i ) = x ⋅ x i

  • (2)多项式核 K ( x , x i ) = ( ( x ⋅ x i ) + 1 ) d

  • (3)径向基核（RBF） K ( x , x i ) = exp ( − ∥ x − x i ∥ 2 σ 2 ) Gauss径向基函数则是局部性强的核函数，其外推能力随着参数 σ 的增大而减弱。多项式形式的核函数具有良好的全局性质。局部性较差。

  • (4)傅里叶核 K ( x , x i ) = 1 − q 2 2 ( 1 − 2 q cos ( x − x i ) + q 2 )

  • (5)样条核 K ( x , x i ) = B 2 n + 1 ( x − x i )

  • (6)Sigmoid核函数 K ( x , x i ) = tanh ( κ ( x , x i ) − δ ) 采用Sigmoid函数作为核函数时，支持向量机实现的就是一种多层感知器神经网络，应用SVM方法，隐含层节点数目(它确定神经网络的结构)、隐含层节点对输入节点的权值都是在设计(训练)的过程中自动确定的。

• 支持向量机的理论基础决定了它最终求得的是全局最优值而不是局部最小值，也保证了它对于未知样本的良好泛化能力而不会出现过学习现象。 核函数的选择 在选取核函数解决实际问题时，通常采用的方法有：

  • 一是利用专家的先验知识预先选定核函数；

  • 二是采用Cross-Validation方法，即在进行核函数选取时，分别试用不同的核函数，归纳误差最小的核函数就是最好的核函数．如针对傅立叶核、RBF核，结合信号处理问题中的函数回归问题，通过仿真实验，对比分析了在相同数据条件下，采用傅立叶核的SVM要比采用RBF核的SVM误差小很多．

  • 三是采用由Smits等人提出的混合核函数方法，该方法较之前两者是目前选取核函数的主流方法，也是关于如何构造核函数的又一开创性的工作．将不同的核函数结合起来后会有更好的特性，这是混合核函数方法的基本思想．

• boostrap是提鞋自举的意思(武侠小说作者所说的左脚踩右脚腾空而起). 它的过程是对样本(而不是特征)进行有放回的抽样, 抽样次数等同于样本总数. 这个随机抽样过程决定了最终抽样出来的样本, 去除重复之后, 占据原有样本的1/e比例.

• 解决多重公线性, 可以使用相关矩阵去除相关性高于75%的变量 (有主观成分). 也可以VIF, 如果VIF值<=4说明相关性不是很高, VIF值>=10说明相关性较高. 我们也可以用 岭回归和lasso回归的带有惩罚正则项的方法. 也可以在一些变量上加随机噪声, 使得变量之间变得不同, 但是这个方法要小心使用, 可能会影响预测效果。

• bias表示模型预测值的均值与样本实际值的差距，它反映了模型对样本数据的拟合能力。bias越低，说明模型越复杂，参数越多，对样本数据的拟合效果越好，但是容易过拟合；bias越高，说明模型越简单，参数太少，对样本数据的拟合效果不好，这就是欠拟合。 降低bias的方法是增加数据的特征维数，从而实现模型参数的增加，提高模型复杂度，增强模型对样本数据的拟合能力，拟合能力越高bias越低。 增加样本数量并没有增加模型训练时的参数，所以不会提高模型复杂度，也就无法降低bias。

• 条件熵越小，信息增益越大。信息增益：Outlook > Humidity > Windy > Temperature，

  • 

• 所谓径向基函数 (Radial Basis Function 简称 RBF), 就是某种沿径向对称的标量函数。 通常定义为空间中任一点x到某一中心点xc之间欧氏距离的单调函数 , 可记作 k(||x-xc||), 其作用往往是局部的 , 即当x远离xc时函数取值很小。最常用的径向基函数是高斯核函数 ,形式为 k(||x-xc||)=exp{- ||x-xc||^2/(2*σ2) } 其中xc为核函数中心,σ为函数的宽度参数 , 控制了函数的径向作用范围。由radial basis: exp(-gamma*|u-v|^2)可知, gamma越小, 模型越简单, 平滑度越好, 分类边界越不容易过拟合.

• 增加树的深度, 会导致所有节点不断分裂, 直到叶子节点是纯的为止. 所以, 增加深度, 会延长训练时间. 决策树没有学习率参数可以调. (不像集成学习和其它有步长的学习方法) 决策树只有一棵树, 不是随机森林

• KNN算法不需要训练参数, 而所有神经网络都需要训练参数, 因此神经网络帮不上忙 . 最简单的神经网络, 感知器, 其实就是线性回归的训练 .可以用一层的神经网络构造对数几率回归

• 只要是和时间序列问题有关的 , 都可以试试HMM,隐马尔科夫(HMM)模型

最后

以上就是朴素树叶为你收集整理的机器学习错题集(1)的全部内容，希望文章能够帮你解决机器学习错题集(1)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。