LeetCode-63. 不同路径 II

103 阅读 0 评论 68 点赞

我是靠谱客的博主健忘画笔，最近开发中收集的这篇文章主要介绍LeetCode-63. 不同路径 II，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目来源
63. 不同路径 II

递归

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int row = obstacleGrid.length-1;
        int col = obstacleGrid[0].length-1;
        return process(row,col,0,0,obstacleGrid);
    }

    private int process(int row ,int col,int i,int j,int[][] obstacleGrid){
        if(i>row || j>col){
            return 0;
        }
        if(obstacleGrid[i][j]==1){
            return 0;
        }
        if(i == row && j==col){
            return 1;
        }
        return process(row,col,i+1,j,obstacleGrid) + process(row,col,i,j+1,obstacleGrid);
    }
}

在这里插入图片描述

动态规划

动规五部曲：

1.确定dp数组（dp table）以及下标的含义

dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。

2.确定递推公式

dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。

因为有了障碍，(i, j)如果就是障碍的话应该就保持初始状态（初始状态为0）。

dp[i][j] = obstacleGrid[i][j]==0?dp[i-1][j]+dp[i][j-1]:0;

3.dp数组如何初始化

因为从(0, 0)的位置到(i, 0)的路径只有一条，所以dp[i][0]一定为1，dp[0][j]也同理。
但如果(i, 0) 这条边有了障碍之后，障碍之后（包括障碍）都是走不到的位置了，所以障碍之后的dp[i][0]应该还是初始值0。
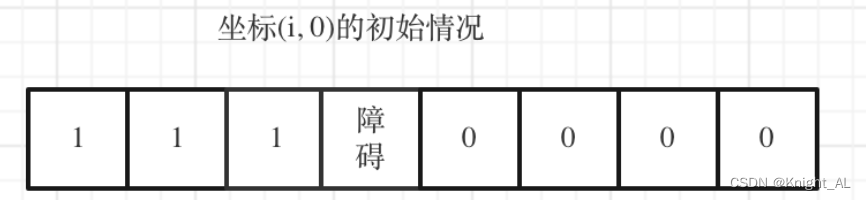
在这里插入图片描述

        for(int i = 0;i<row && obstacleGrid[i][0]==0;i++){
            dp[i][0] = 1;
        }
        for(int j = 0;j<col && obstacleGrid[0][j]==0;j++){
            dp[0][j] = 1;
        }

注意代码里for循环的终止条件，一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作，dp[0][j]同理

4.确定遍历顺序

从递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 中可以看出，一定是从左到右一层一层遍历，这样保证推导dp[i][j]的时候，dp[i - 1][j] 和 dp[i][j - 1]一定是有数值。

        for(int i = 1;i<row;i++){
            for(int j = 1;j<col;j++){
                dp[i][j] = obstacleGrid[i][j]==0?dp[i-1][j]+dp[i][j-1]:0;
            }
        }

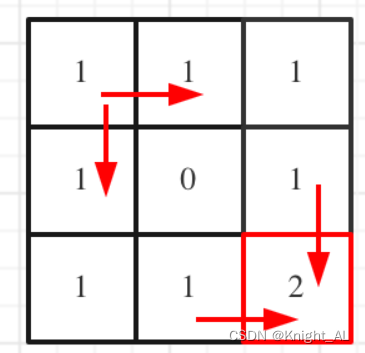
5.举例推导dp数组

对应的dp table 如图：

在这里插入图片描述
完整代码

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int row = obstacleGrid.length;
        int col = obstacleGrid[0].length;
        int[][] dp = new int[row][col];
        for(int i = 0;i<row && obstacleGrid[i][0]==0;i++){
            dp[i][0] = 1;
        }
        for(int j = 0;j<col && obstacleGrid[0][j]==0;j++){
            dp[0][j] = 1;
        }
        for(int i = 1;i<row;i++){
            for(int j = 1;j<col;j++){
                dp[i][j] = obstacleGrid[i][j]==0?dp[i-1][j]+dp[i][j-1]:0;
            }
        }
        return dp[row-1][col-1];
    }
}