2021 acm-icpc区域赛(上海)补题笔记

前言

赛前打几场重现赛模拟一下，争取把力所能及的题都补了

yysy，今年大部分赛站卷的程度已经非往年可比的了…

比赛链接：https://ac.nowcoder.com/acm/contest/24872

题目一览

签到题：D,E,G,I

铜牌题：H

银牌题：J,K,M

金牌题：B

大概不是我能做的题：A,C,F,L

本场差不多是5题铜，6.5题银，8题金

D.Strange_Fractions(签到)

题意

思路

初中数学，设 $x=\frac{a}{b}$ , 有 $\frac{p}{q}=x+\frac{1}{x}$ , 求根公式解出来即可。

E.Strange_Integerss(签到)

题意

从 n 个数中选出 m 个数使得两两之差绝对值不低于 k ， 要求最⼤化 m 。

11 2
3 1 4 1 5 9 2 6 5 3 5

4

思路

排序后从⼩到⼤贪⼼选取合法且尽可能接近的数字即可

G.Edge Groups（树形dp)

题意

求树分解成若⼲⻓度为2 的路径的⽅案数。

7
1 2
1 3
1 7
4 7
5 7
6 7

3

思路

很板子的树dp，队友写的，没看。官方题解：

I.Steadily Growing Steam(背包)

题意：

题目有点长，大意是：

n件物品具有体积 $t_i$ 和价值 $v_i$ ，选出⾄多 $k$ 件物品 将其体积翻倍，然后选出若⼲物品并将其分为 体积和 相同的两堆$S,T$，问选出的物品 价值之和 最⼤是多少。

输入

4 1
10 1
-5 3
5 1
6 1

输出

21

One possible scheme:

Double $t_1$ and choose that S = { 1 } , T = { 3 , 4 } S={1},T={3,4} S={1},T={3,4}, where the point number sum are both 2, and the sum of the card values is $10+5+6=21$.

思路：

很显然是01背包，其实挺签到的，但却把我们卡了一个多钟。

主要是一直在想两个集合怎么相互转移的问题。

后来想到两个集合是可以合并的。

我们假设装进集合S的物品体积为 $+t_i$ , 那么可以假设装进集合T的物品体积为 $-t_i$ ,这样动态转移的终点就会在体积和 $V=0$ 处了。

具体地，设 $dp[N][V][K]$ 表示当前在第i个物品 ， 体积和为V，已经将K件物品翻倍。

然后第$i$个物品只会从第 $i-1$ 个物品转移，所以第一维的N可以用滚动数组滚掉，变成 $dp[2][V][K]$.

我们将每个物品拆分成四个：

$aa=(v_i,t_i)$ ,$bb=(v_i,-t_i)$

$cc=(v_i,2\ast t_i),$$dd=(v_i,-2\ast t_i)$

那么：

$dp[i][V][K]=max(dp[i][V][K],dp[i\oplus 1][V-aa][j]+v[i])$

$dp[i][V][K]=max(dp[i][V][K],dp[i\oplus 1][V-bb][j]+v[i])$

$dp[i][V][K]=max(dp[i][V][K],dp[i\oplus 1][V-cc][j-1]+v[i])$ $,K>0$

$dp[i][V][K]=max(dp[i][V][K],dp[i\oplus 1][V-dd][j-1]+v[i])$ $,K>0$

代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 111;
int dp[2][5555][111];
int n,k;
int v[N],t[N];
signed main(){
    ios::sync_with_stdio(false);
    cin>>n>>k;
    for(int i=1;i<=n;i++){
        cin>>v[i]>>t[i];
    }
    for(int i=0;i<=5500;i++)
        for(int j=0;j<=110;j++)
            dp[0][i][j] = dp[1][i][j] = -1e15;
        int now = 0,ans = 0;
        dp[now][2800][0] = 0;
        for(int i=1;i<=n;i++){
            now = now^1;
            int aa = t[i],bb = -t[i],cc = 2*t[i],dd = -2*t[i];
            for(int V=-2600;V<=2600;V++){
                for(int j=0;j<=k;j++){
                    int tmp = V+2800;
                    dp[now][tmp][j] = dp[now^1][tmp][j];
                    dp[now][tmp][j] = max(dp[now][tmp][j],dp[now^1][tmp-aa][j]+v[i]);
                    dp[now][tmp][j] = max(dp[now][tmp][j],dp[now^1][tmp-bb][j]+v[i]);
                    if(k>0){
                        dp[now][tmp][j] = max(dp[now][tmp][j],dp[now^1][tmp-cc][j-1]+v[i]);
                        dp[now][tmp][j] = max(dp[now][tmp][j],dp[now^1][tmp-dd][j-1]+v[i]);
                    }
                    ans = max(ans,dp[now][tmp][j]);
                }
            }
        }
        cout<<ans<<endl;
}

H.Life is a Game (kruskal重构树+树上倍增)

题意：

⼀张带边权带点权⽆向图。从某点出发，有初始声望。 每第⼀次到达⼀个点将获得点权等值的声望加成。

经过⼀条边需要满⾜边权等值的最低声望限制。 多次给出起点和初始声望，询问能达到的最⼤声望。

思路：

铜牌题越来越难了啊。

我们不会kruskal重构树，那天用堆+启发式合并硬搞出来的。

现在补题主要写一写kruskal重构树的解法，毕竟可以离线做这道题。

洛谷上的kruskal重构树：https://www.luogu.com.cn/problem/P7834 （不过洛谷这题加了主席树维护第k大）

其实就是在kruskal的过程中建树：

把边按边权从小到大排序，并查集合并两端点$u,v$ 的同时新建一个节点$tot$ , 节点$tot$连接$u,v$ , 且维护$u,v$点的共同信息

在本题中 ， $tot$ 节点可以维护两个信息 ，$a_u+a_v$ 和 $w(u,v)$ 。

本题的感想是kruskal重构树是一个很好的思路，它用很少的时间和空间维护了并查集的一些关键信息。

样例的重构树长这样：

然后树上倍增维护每个节点的第i级父节点，查询的时候倍增地查就好了。

官方解答：

代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5+100;
struct node{
    int u;
    int v;
    int w;
    bool operator<(node B) const{
        return w<B.w;
    }
}e[N<<1];
int a[N<<1];
int n,m,q;
int fa[N<<1];
vector<int> g[N<<1];
int val[N<<1];
int ff[N<<1][22];
int tot;
int find_fa(int x){
    return (fa[x]==x)?fa[x]:fa[x] = find_fa(fa[x]);
}
void Kruskal(){
    tot = n;
    for(int i=1;i<=m;i++){
        int u = find_fa(e[i].u),v = find_fa(e[i].v),w = e[i].w;
        if(find_fa(u)!= find_fa(v)){
            tot++;
            val[tot] = w;
            g[tot].push_back(u);
            g[tot].push_back(v);
            g[u].push_back(tot);
            g[v].push_back(tot);
            fa[u] = fa[v] = fa[tot] = tot;
        }
    }
}
void dfs(int u,int f){
    ff[u][0] = f;
    for(int i=1;i<=20;i++){
        ff[u][i] = ff[ff[u][i-1]][i-1];
    }
    for(auto v:g[u]){
        if(v==f) continue;
        dfs(v,u);
        a[u] += a[v];
    }
}
signed main(){
    ios::sync_with_stdio(false);
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++) cin>>a[i],fa[i] = i;
    for(int i=1;i<=m;i++){
        int x,y,z;
        cin>>x>>y>>z;
        e[i] = {x,y,z};
    }
    sort(e+1,e+1+m);
    Kruskal();
    dfs(tot,0);
    val[0] = 1e15+7;
    while(q--){
        int u,x;
        cin>>u>>x;
        int now = x+a[u];
        while(now!=tot){
            //cout<<u<<" "<<x<<endl;
            bool ok = false;
            for(int i=20;i>=0;i--){
                if(val[ff[u][i]]<=now){
                    u = ff[u][i];
                    ok = true;
                }
            }
            if(!ok) break;
            now = x+a[u];
        }
        cout<<now<<endl;
    }
    return 0;
}

K.Circle of Life(打表+构造)

题意

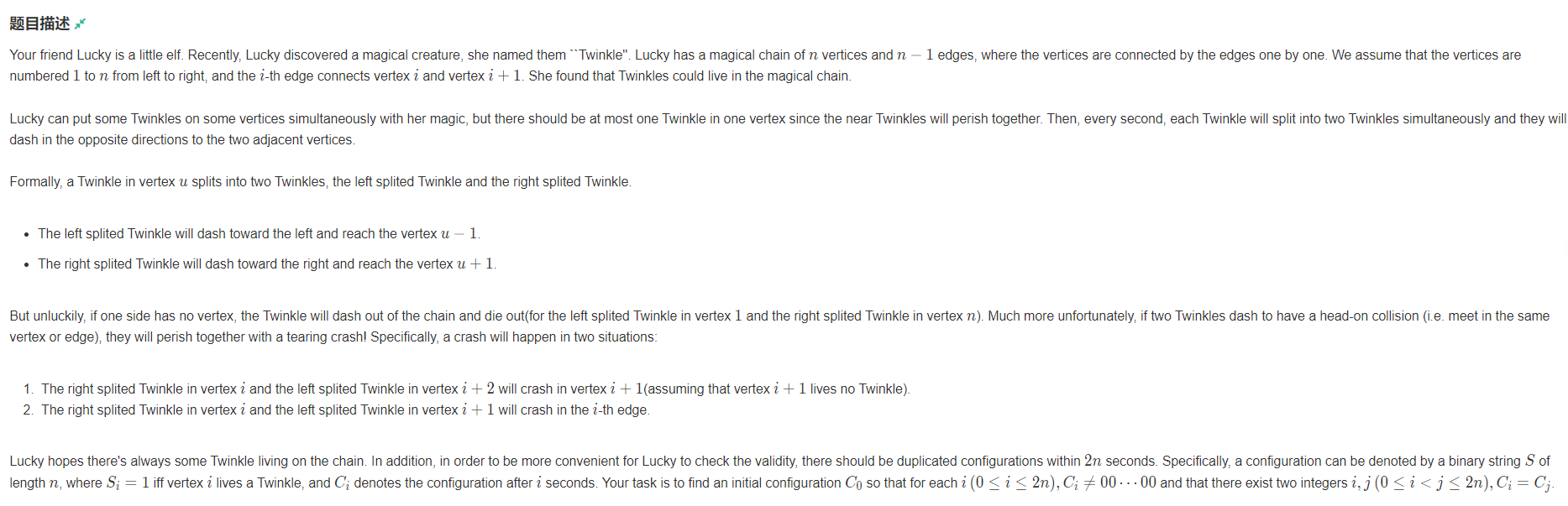
思路

找规律题，感觉如果把重构树写完还能剩一些时间的话大概率都能写写这题。。。

把题意模拟出来，然后发现是构造

发现n = 6时只有两种解：100110，（另一个忘了）

然后以这两个为主去找规律，发现1001可以作为循环节，然后没了。

代码：

#include<bits/stdc++.h>
using namespace std;
string s[4] = {"1001","10001","100110","1001010"};
int main(){
    ios::sync_with_stdio(false);
    int n;
    cin>>n;
    if(n==2){
        cout<<"10"<<endl;
    }
    else if(n==3){
        cout<<"Unlucky"<<endl;
    }
    else if(n<=7){
        cout<<s[n-4]<<endl;
    }
    else{
        int tot = (n-4)/4;
        int res = (n-4)%4;
        for(int i=0;i<tot;i++) cout<<"1001";
        cout<<s[res]<<endl;
    }
}

J.Two Binary Strings Problem（bitset+位运算）

题意：

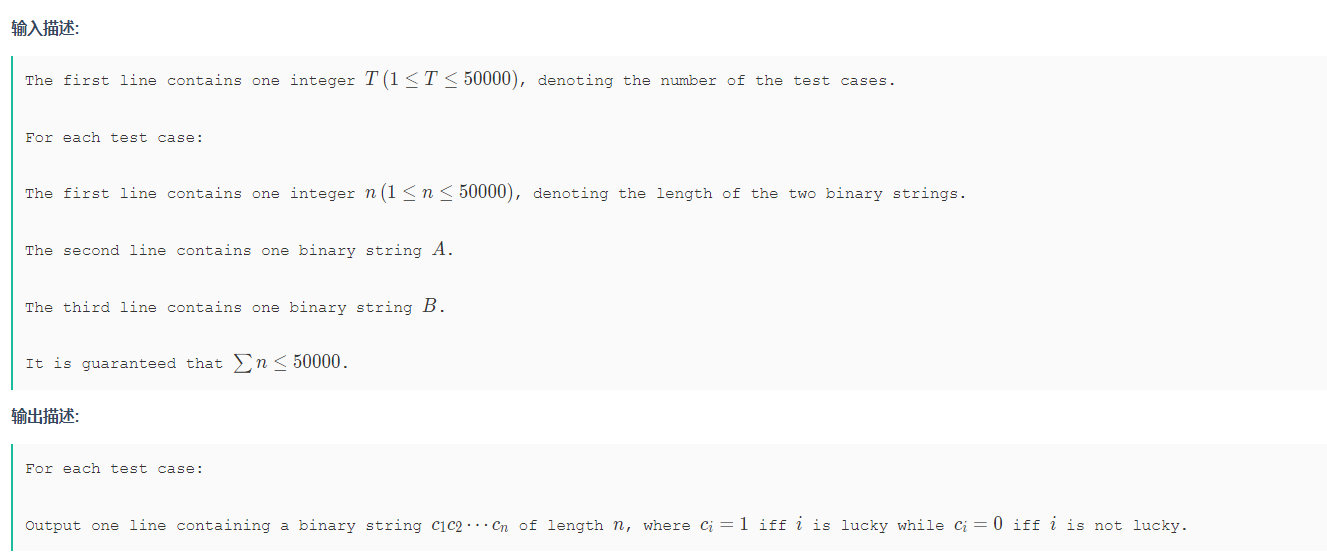
输入

2
5
11010
11000
8
11110000
11111100

输出

01000
00001100

思路：

会不会用bitset决定了这题能不能写。。。。

很显然，打暴力的话复杂度是 $O（n^2)$

对于32位整型INT ， 用bitset通过位运算打暴力的复杂度是 $O(\frac{n^2}{32})$

但是细节很多，对着逆十字的代码看了半天才弄明白。。。

把0变成-1，然后维护前缀和$sum[]$

把前缀和排个序，大的在前面

然后按顺序遍历一遍

于是惊奇的发现，如果前面访问的位置$i$比之后访问的位置$j$小，那么$j$这个位置肯定是不行的

因为既然有 $sum[i]>sum[j]$ 且 $i<j$

那么就必然存在一个 $k$ ,使得 $sum[j]-sum[j-k]<=0$ ,也就是 $[j-k,j]$ 这个区间的0不比1少

所以开一个bitset A ， 把顺序遍历时对应的位置pos标上，代表该位置被访问了。

对于 $b[i]=0$ 的情况，其实就是将$b[i]=1$时的各项取反

那么再开一个bitset one,置为全1 ， 因为二进制数 异或 全1就是取反。

然后一个bitset ans 记录答案，每次遍历时拿bitset A 更新ans.

代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 50500;
char a[N],b[N];
int s[N],id[N];
bitset<N> A,ans,one;
bool cmp(int xx,int yy){
    return s[xx]==s[yy]?xx<yy:s[xx]>s[yy];
}
int main(){
    ios::sync_with_stdio(false);
    int t;
    cin>>t;

    while(t--){
        A.reset(),ans.reset(),one.reset();
        int n;
        cin>>n;
        cin>>(a+1);
        cin>>(b+1);
        int tg = n+1;
        for(int i=1;i<=n;i++) one[i] = 1;
        id[0] = 0;
        for(int i=1;i<=n;i++){
            s[i] = s[i-1]+((a[i]=='1')?1:-1);
            id[i] = i;
        }
        sort(id,id+1+n,cmp);
        for(int i=0;i<=n;i++){
            int pos = id[i];
            if(pos) {
                if (b[pos] == '1') {
                    ans = ans | (A >> (n - pos));
                    if (s[pos] <= 0) tg = min(tg, pos + 1);
                } else {
                    ans = ans | ((A ^ one) >> (n - pos));
                    if (s[pos] > 0) tg = min(tg, pos + 1);
                }
            }

            A[n-pos] = 1;
        }
        for(int i=1;i<=n;i++){
            if(ans[i]||i>=tg) cout<<0;
            else cout<<1;
        }
        cout<<endl;
    }
}

B.Strange Permutations （生成函数 / NTT+容斥）

呜呜呜，不会生成函数，不会快速傅里叶变换，不会数论变换

呜呜呜，我怎么什么都不会呀

有空再更吧。。。。

---

2022-4-5 我来补作业了.jpg

题意

在 $1--n$的排列中，给出了$n$个限制：

$(i,p_i)$不能为排列中的相邻元素 ， 问有多少个满足条件的排列？

输入

4
3 4 1 2

输出

8

给出的限制为 ：

 (1,3),(2,3),(3,1),(4,2)

满足的排列为：

{1,2,3,4} {1,4,3,2} {2,1,4,3} {2,3,4,1}
{3,2,1,4} {3,4,1,2} {4,1,2,3} {4,3,2,1}

思路

类似于在完全图中找一条经过$n$ 个点的哈密顿路 ，其中有$n$ 条边禁选。

首先是一个经典容斥问题：

$an{s}_i$表示选择了 $i$ 条禁选边的方案数

那么 ，答案就是 $sum={\sum }_{i=0}^n(-1{)}^i\ast an{s}_i\ast (n-i)!$

现在问题变成了如何求 $an{s}_i$

显然我们选边不能乱选，因为可能会成环。

可以知道，所有的禁选边会组成 若干个环,我们可以在每个环中取最多 “环的边数-1” 条边。

也就是说，现在有 $n$ 个环 $s{r}_1,s{r}_2,s{r}_3,...s{r}_n$。

我们可以在第1个环中取 {0, 1 ,2 ,3 ,… ,$s{r}_n-1$} 条边，对应的组合数是：

$F(1)$ = [$C_{s{r}_1}^0$ $C_{s{r}_1}^1$ $C_{s{r}_1}^2$ $C_{s{r}_1}^3$ … … $C_{s{r}_1}^{s{r}_1-1}$ ]

同理，对于其它环，对应的组合数是：

$F(2)$ = [$C_{s{r}_2}^0$ $C_{s{r}_2}^1$ $C_{s{r}_2}^2$ $C_{s{r}_2}^3$ … … $C_{s{r}_2}^{s{r}_2-1}$ ]

$F(3)$ = [$C_{s{r}_3}^0$ $C_{s{r}_3}^1$ $C_{s{r}_3}^2$ $C_{s{r}_3}^3$ … … $C_{s{r}_3}^{s{r}_3-1}$ ]

…

$F(n)$ = [$C_{s{r}_n}^0$ $C_{s{r}_n}^1$ $C_{s{r}_n}^2$ $C_{s{r}_n}^3$ … … $C_{s{r}_n}^{s{r}_n-1}$ ]

那么，我们将他们都卷积起来对应的位置 $i$ 就是取 $i$ 个数的答案 $an{s}_i$ 呀 (好像和生成函数没啥关系.jpg)

代码

#include<bits/stdc++.h>
using namespace std;
#define int long  long
const int N = 8e5+100;
const int mod = 998244353;
struct E{
    int to;
    int nxt;
}e[N<<1];
int head[N],tot;
bool vis[N<<1];
int fac[N],inv[N];
vector<int> sr;
int ksm(int a,int b,int p){
    int ans = 1;
    while(b){
        if(b&1ll){
            ans = ans*a%p;
        }
        a = a*a%p;
        b>>=1;
    }
    return ans;
}
void pre(){
    fac[0] = 1;
    for(int i=1;i<=200000;i++){
        fac[i] = fac[i-1]*i%mod;
    }
    inv[200000] = ksm(fac[200000],mod-2,mod)%mod;
    for(int i=200000-1;i>=0;i--)
        inv[i] = inv[i+1]*(i+1)%mod;
}
int C(int n,int m){
    return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
void add_edge(int u,int v){
    e[++tot].nxt =head[u];
    e[tot].to = v;
    head[u] = tot;
}
void dfs(int u,int rt,int sum){
    for(int i=head[u];i;i=e[i].nxt){
        int v = e[i].to;
        if(vis[i]) continue;
        vis[i] = true;
        if(v==rt){
            sr.push_back(sum);
            return;
        }
        dfs(v,rt,sum+1);
    }
}

struct NTT{
    int a[N],b[N];
    int r[N];
    int n;
    void fft(int *x,int opt){
        int i,j,k,m,gn,g,tmp;
        for(i=0;i<n;i++)
            if(r[i]<i) swap(x[i],x[r[i]]);
        for(m=2;m<=n;m<<=1){
            k = m>>1;
            gn = ksm(3,(mod-1)/m,mod);
            for(i=0;i<n;i+=m){
                g = 1;
                for(j=0;j<k;j++,g = g*gn%mod){
                    tmp = x[i+j+k]*g%mod;
                    x[i+j+k] = (x[i+j]-tmp+mod)%mod;
                    x[i+j] = (x[i+j]+tmp)%mod;
                }
            }
        }
        if(opt==-1){
            reverse(x+1,x+n);
            int invv = ksm(n,mod-2,mod);
            for(i=0;i<n;i++)
                x[i] = x[i]*invv%mod;
        }
    }
    void init(int len,vector<int> _a,vector<int> _b){
        int m;
        for(n=1,m=0;n<=len;n<<=1,m++);
        for(int i=0;i<n;++i){
            r[i]=r[i>>1]>>1|(1ll&i)<<(m-1);
            a[i]=b[i]=0;
        }
        for(int i=0;i<_a.size();i++)
            a[i] = _a[i];
        for(int i=0;i<_b.size();i++)
            b[i] = _b[i];
    }
    void cal(){
        fft(a,1);
        fft(b,1);
        for(int i=0;i<n;i++)
            a[i] = a[i]*b[i]%mod;
        fft(a,-1);
    }
    vector<int> cdq(int L,int R){
        if(L==R){
            vector<int> now;
            for(int i=0;i<sr[L];i++)
                now.push_back(C(sr[L],i));
            return now;
        }
        int mid = (L+R)>>1;
        vector<int> aa = cdq(L,mid);
        vector<int> bb = cdq(mid+1,R);
        init(aa.size()+bb.size()-1,aa,bb);
        cal();
        vector<int> ans;
        for(int i=0;i<aa.size()+bb.size()-1;i++)
            ans.push_back(a[i]);
        return ans;
    }
}nt;
signed main(){
    ios::sync_with_stdio(false);
    pre();
    int n;
    cin>>n;
    sr.push_back(0);
    for(int i=1;i<=n;i++){
        int x;
        cin>>x;
        add_edge(i,x);
    }
    for(int i=1;i<=n;i++){
        dfs(i,i,1);
    }
    vector<int> ans = nt.cdq(1,sr.size()-1);
    int sum = 0;
    for(int i=0;i<ans.size();i++){
        if(i&1ll) sum = (sum-ans[i]*fac[n-i]%mod+mod)%mod;
        else sum = sum+ans[i]*fac[n-i]%mod;
    }
    cout<<sum%mod<<endl;
}

最后

以上就是结实抽屉为你收集整理的2021 acm-icpc区域赛(上海)补题笔记的全部内容，希望文章能够帮你解决2021 acm-icpc区域赛(上海)补题笔记所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。