G.Edge Groups-2021-ICPC上海站

80 阅读 0 评论 53 点赞

我是靠谱客的博主长情老鼠，最近开发中收集的这篇文章主要介绍G.Edge Groups-2021-ICPC上海站，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目大意

给你一棵n个节点的树，n为奇数，问将所有边两两分成一组，且每组的两条边有一个公共点，有多少方案数。

树形DP

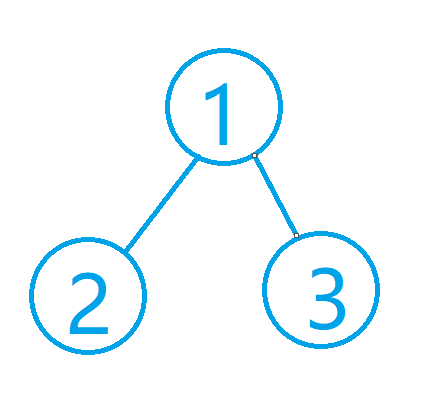
在这里插入图片描述
首先分析最基本的情况，这种情况下只有一组，接下来增加叶节点个数

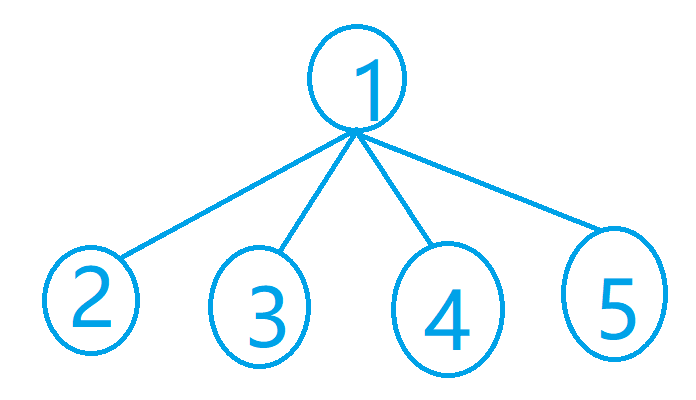
在这里插入图片描述
当有四个节点时，我们可以分析发现，有3×1种方案（2可以与3,4,5分别组队，公共点为1，当2与其他节点组队后，剩下的两个节点只有一种组队方案）,扩展到6个节点的情况下可以以相同的方式推理。

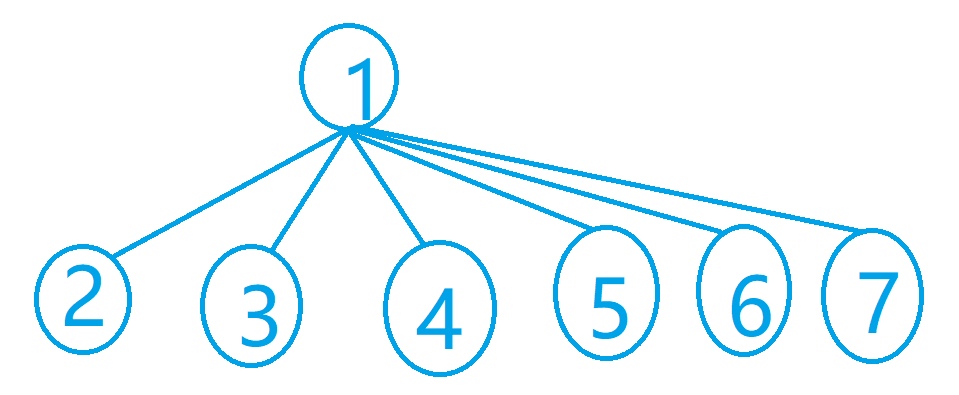
在这里插入图片描述
2可以与3,4,5,6,7组队，则此时剩下4个叶节点，最终的方案数量为（5×3×1）。可以发现，当根节点下有偶数个叶节点时，不会用到根节点与根节点的父节点的那条边（并且不能用到，否则这个根节点的叶节点不能全部匹配了）

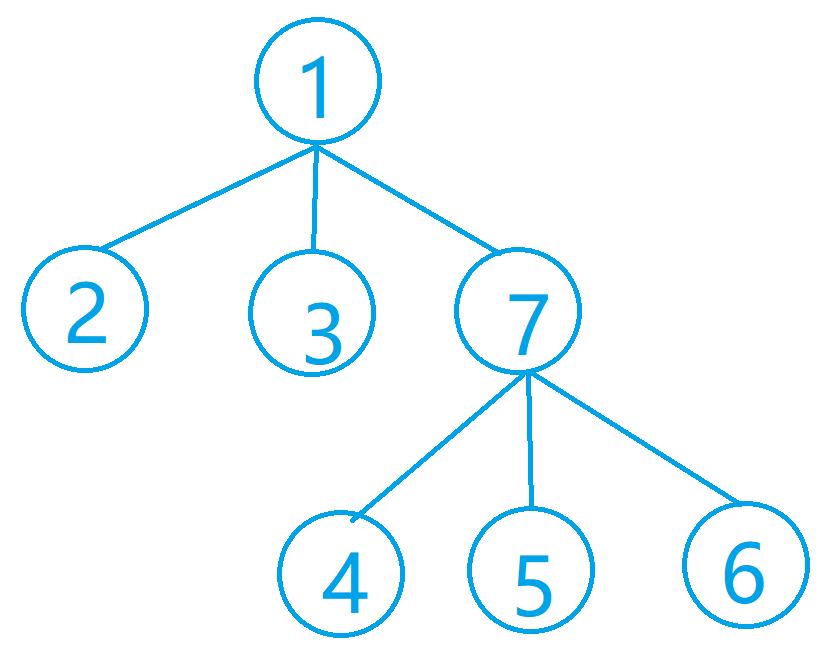
在这里插入图片描述
如节点7所示，有三个叶节点，无论如何匹配都需要用到7-1的这条边，那么当考虑1的子节点的匹配时，不能考虑1-7的这条边，而计算以7位根节点的匹配方案数量时，就需要将7的叶节点边数加1。然后计算所有奇数的乘积。
（7节点共三个叶节点，3是奇数，匹配时要带上7的父节点的那条边，最终的计算结果为3×1）

当计算1的时候，需要忽略1-7的这条边，因为这条边不能与1的其他节点再匹配了，最终的结果应该是1的可以匹配的节点的方案数乘上下面匹配过的节点的方案数量。
（1×(3×1)）

代码实现
f[N]数组记录i节点下的匹配方案数，1作为根节点。
从根节点开始广搜，函数返回值为这条边能不能用来匹配，如果可以用来匹配那么用cnt变量来记录下，搜完所有的边后乘上这一层的匹配量。

#include <iostream>
#include <cstring>

using namespace std;
using ll = long long;

const int N = 1e5 + 10, M = 2 * N;
const int mod = 998244353;

int h[N], e[M], ne[M], idx;
ll f[N];
int n;

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

bool bfs(int u, int fa)
{
    f[u] = 1;
    int cnt = 0;
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (j == fa) continue;
        if (bfs(j, u)) // 如果不用借用父边，那么cnt记录下
        {
            cnt++;
        }
        f[u] = f[u] * f[j] % mod;
    }
    if (cnt % 2) // 奇数, 需要借用父边
    {
        for (int i = cnt + 1; i >= 2; i -= 2)
        {
            f[u] = (i - 1) * f[u] % mod;
        }
    }
    else
    {
        for (int i = cnt; i >= 2; i -= 2)
        {
            f[u] = (i - 1) * f[u] % mod;
        }
    }
    return (cnt % 2 == 0); 
    // 如果可以用来匹配的边个数为偶数，那么就是可以用它和根节点的那条边 
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n;
    for (int i = 1; i < n; i++)
    {
        int a, b;
        cin >> a >> b;
        add(a, b);
        add(b, a);
    }
    bfs(1, -1); // 1作为根节点，根节点没有父节点，父节点为-1
    cout << f[1] << endl;
    return 0;
}