The Preliminary Contest for ICPC Asia Nanjing 2019
【A. The beautiful values of the palace】
【题目大意】
有一个n * n的矩阵,n为奇数,矩阵中的数字为n * n的正序排列,且顺时针增大,左下角标号(1, 1),右上角标号(n, n)

现在告诉你矩阵中有m个数字被标记,并给出了标记数字的标号,然后给出p个询问,每个询问包括一个子矩阵的左下角下标和右上角下标,问你在该子矩阵中被标记的数字的各个位数之和为多少
即 25 = 2 + 5,18 = 1 + 8
问你所有的数字的和为多少
【解题思路】
首先第一步,要想求和,首先得知道数字与标号间的关系,考虑将矩阵分为n个圈层,每一层按顺时针增大
如上图第一层:

可以发现,每一圈层最后一个数字是由右上角第一个数子加上4次(n - 圈层数)得到的
那么定义圈层标号为t(从右至左依次为1,2,3…),圈层开始的数字为s,则其迭代式为:
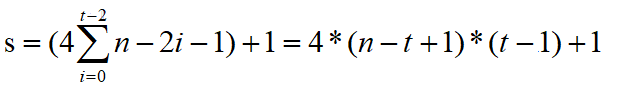
而对于任一圈,开头数字的坐标永远是(n - t +1, n - t +1),那么即可根据对应坐标推出相应数字
inline ll Getnum(ll x, ll y) {
ll t = min(min(x, y), min(n - x + 1, n - y + 1)); //找到该坐标所在的圈层数
ll res = 4 * (t - 1) * (n - t + 1);
if (n - x + 1 == t) res += n - t - y + 2; //在圈层的右边
else if (y == t) res += 2 * n - 3 * t - x + 3; //在圈层的下边
else if (x == t) res += 2 * n - 5 * t + y + 3; //在圈层的左边
else res += 3 * n - 7 * t + x + 4; //在圈层的上边
return res;
}
那么对于每一个数字,我们便可以预先处理出他的各位数之和
数字搞定了,再来看怎么求和,暴力显然超时,我们可以考虑用树状数组对区间进行离散化
首先我们已知需要求解的区间为(x1, y1),(x2, y2),我们把它分为四个区间,处理坐标(1, 1)与(xi, yi)的区间和,利用前缀的思想不难想到
S = S(x2, y2) - S(x1 - 1, y2) - S(x2, y1 - 1) +S(x1, y1)
其中S为待求区间,S(xi, yi)表示(1, 1)与(xi, yi)形成的区间
那么我们利用扫描线的思想,想像有一条平行于y轴的直线从左往右进行扫描,每遇到一个标记数字就将其加入树状数组,每遇到一个待求区间就GetSum
但是,如何保证单调性才是问题的关键,树状数组是一种离线做法,那么我们可以将所有的区间和点优先按x升序,次先按y升序,如果点和区间的坐标相同,那么按点优先进行排序,则可以保证是单调的
证明:
首先对于x,按照扫描线,优先从x小的开始处理,则按x升序保证了x轴上的单调性
其次对于y,由于优先将点加入树状数组,那么在处理区间时,一定是从小至大依次处理,且处理区间前一定可以保证区间内的所有点都已经处理完毕,保证了y轴的单调性
那么区间和点的单调性显然保证
证毕
对于区间和点的区分可以按照离散化的处理时间进行区分
还有一些细节建议结合代码查看
【AC代码】
#include <bits/stdc++.h>
#define lowbit(x) ((x) & (-(x)))
using namespace std;
typedef long long ll;
const int maxn = 4e6 + 10;
struct Palace {
int x, y, val; //坐标和数字
int id; //记录离散化的时间
int flag; //标记区间的+、-
Palace() { flag = x = y = val = id = 0; }
Palace(int mx, int my, int mval, int mid, int mflag) :x(mx), y(my), val(mval), id(mid), flag(mflag) {}
inline bool operator < (const Palace& b)const {
if (x == b.x) {
if (y == b.y) {
return id < b.id;
}
return y < b.y;
}
return x < b.x;
} //排序保证单调性
}a[maxn]; //记录点和坐标的信息,可以看作一个队列
ll b[maxn]; //记录y轴上的一维区间和
ll c[maxn]; //离线记录答案最后输出
ll n, m, p;
inline ll min(ll a, ll b) { return a < b ? a : b; }
inline void Update(int i, ll k) { //树状数组单点更新,用于添加点
while (i <= n) {
b[i] += k;
i += lowbit(i);
}
}
inline ll Getsum(int i) { //树状数组区间求和
ll res = 0;
while (i > 0) {
res += b[i];
i -= lowbit(i);
}
return res;
}
inline ll Getnum(ll x, ll y) { //根据坐标获取数字
ll t = min(min(x, y), min(n - x + 1, n - y + 1));
ll res = 4 * (t - 1) * (n - t + 1);
if (n - x + 1 == t) res += n - t - y + 2;
else if (y == t) res += 2 * n - 3 * t - x + 3;
else if (x == t) res += 2 * n - 5 * t + y + 3;
else res += 3 * n - 7 * t + x + 4;
return res;
}
inline void init() { //清空数组
memset(b, 0, sizeof(b));
memset(c, 0, sizeof(c));
}
int main() {
int t;
scanf("%d", &t);
while (t--) {
init();
scanf("%lld%lld%lld", &n, &m, &p);
for (int i = 1; i <= m; ++i) {
a[i].val = 0; //别忘了一开始数字置0
scanf("%d%d", &a[i].x, &a[i].y);
ll temp = Getnum(a[i].x, a[i].y);
while (temp) { //求得各个位数之和
a[i].val += temp % 10;
temp /= 10;
}
a[i].id = i; //记录点的离散化时间
}
int cnt = m;
for (int i = 1; i <= p; ++i) {
int x, y, xx, yy;
scanf("%d%d%d%d", &x, &y, &xx, &yy); //对区间进行离散化,分为4个区间,且四个区间离散化时间必须相同
a[++cnt] = Palace(x - 1, y - 1, 0, i + m, 1); //符号为+
a[++cnt] = Palace(xx, y - 1, 0, i + m, -1); //符号为-
a[++cnt] = Palace(x - 1, yy, 0, i + m, -1); //符号为-
a[++cnt] = Palace(xx, yy, 0, i + m, 1); //符号为+
}
sort(a + 1, a + cnt + 1);
for (int i = 1; i <= cnt; ++i) { //扫描线遍历
if (a[i].id <= m) { //遇到的是点,更新树状数组
Update(a[i].y, a[i].val);
}
else { //否则对树状数组进行求和,并更新该区间的答案
c[a[i].id - m] += Getsum(a[i].y) * a[i].flag;
}
}
for (int i = 1; i <= p; ++i) { //离线输出答案
printf("%lldn", c[i]);
}
}
return 0;
}
【B. super_log】
【题目大意】
给定一个函数定义如下:
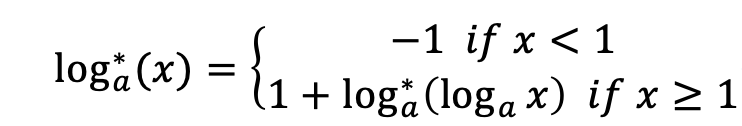
给定a,b,m,问最小的x,使得
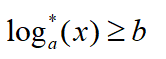
输出x % m的结果
【解题思路】
稍加模拟不难发现

根据拓展欧拉定理降幂即可
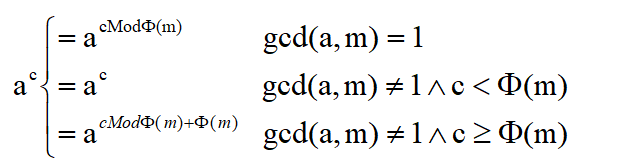
【AC代码】
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a, b, p;
inline ll Mod(ll x, ll p) { //欧拉重定义模运算
return x < p ? x : (x % p + p);
}
inline ll QuickPower(ll a, ll b, ll p) { //快速幂
ll res = 1;
while (b) {
if (b & 1) res = Mod(res * a, p);
a = Mod(a * a, p);
b >>= 1;
}
return res;
}
inline ll euler_phi(ll n) { //欧拉函数
ll m = sqrt(n);
ll ans = n;
for (int i = 2; i <= m; ++i) {
if (n % i == 0) {
ans -= ans / i;
while (n % i == 0) n /= i;
}
}
if (n > 1) ans -= ans / n;
return ans;
}
inline ll solve(ll b, ll p) {
if (b == 1 || p == 1) return Mod(a, p);
return QuickPower(a, solve(b - 1, euler_phi(p)), p);
}
int main() {
int t;
scanf("%d", &t);
while (t--) {
scanf("%lld%ld%lld", &a, &b, &p);
if (a == 1 || b == 0) {
printf("%lldn", 1 % p);
}
else if (b == 1) {
printf("%lldn", a % p);
}
else printf("%lldn", solve(b, p) % p);
}
return 0;
}
【F. Greedy Sequence】
【题目大意】
有多组样例,每组给定序列长度n和一个长度k,给定一个n个数的排列a,问你能够构造出来的序列Si的最大长度为多少,其中Si的定义如下:
1.Si[1] = i
2.Si[j] ≤ Si[j - 1]
3.对于任意的j,Si[j]属于序列a,且在a中的下标距离i在a中的下标超过k
求每一个1 - n的Si的最大序列长度
【解题思路】
有人用主席树,有人用线段树,但是这里我想直接暴力
考虑记录a中每个数字对应的下标,根据动态规划的思想,对于序列Si,如果i - 1距离i不超过k,那么显然Si的序列长度为Si - 1加上1,S1长度显然为1,那么从后往前遍历i,找到距离i不超过k的Si-j的序列长度,再加上1即为Si的序列长度

【AC代码】
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
int a[maxn];
int ans[maxn];
inline int read() //快读
{
register int X = 0, w = 0; register char ch = 0;
while (!isdigit(ch)) { w |= ch == '-'; ch = getchar(); }
while (isdigit(ch)) X = (X << 3) + (X << 1) + (ch ^ 48), ch = getchar();
return w ? -X : X;
}
inline void write(register int x) //快写
{
if (x < 0) putchar('-'), x = -x;
if (x > 9) write(x / 10);
putchar(x % 10 + '0');
}
int main() {
register int t;
t = read();
while (t--) {
register int n, k;
n = read(), k = read();
for (register int i = 1; i <= n; ++i) {
register int x;
x = read();
a[x] = i;
}
for (register int i = 1; i <= n; ++i) {
ans[i] = 1;
for (register int j = i - 1; j >= 1; --j) {
if (abs(a[j] - a[i]) <= k) {
ans[i] = ans[j] + 1;
break;
}
}
write(ans[i]);
if (i == n) puts("");
else putchar(' ');
}
}
return 0;
}
【H. Holy Grail】
【题目大意】
给定有向图G = (n, m),再给你6条边,问你怎么设定这6条边的权值使得图中不产生负环且权值最小(权值可以为负),按顺序输出这6条边的权值,保证在加边之前不存在该边且答案保证存在
【解题思路】
对于G = (n, m),我们可以先求出所有节点间的最短路,考虑要使得权值最小且不产生负环,那么假设要添加的边w = (u, v),那么显然在添加w之前存在一条路径使得v能够到达v,否则答案不存在,那么加入w后图中一定会产生环,则有:
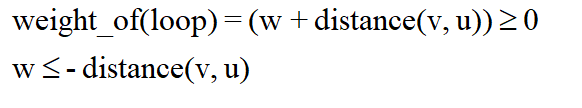
那么答案即为-G[v][u]
注意每一次加入边权后都要重新求解最短路
由于n最大300,直接Floyd,时间复杂度O(T * 6 * n3) = O(810 * 106)
实测684ms
【AC代码】
#include <bits/stdc++.h>
#define Rep(i, n) for(register int i = 0; i < (n); ++i)
using namespace std;
const int INF = 0x3f3f3f3f;
int G[310][310];
struct Edge { int x, y; }edge[7];
inline int read()
{
register int X = 0, w = 0; register char ch = 0;
while (!isdigit(ch)) { w |= ch == '-'; ch = getchar(); }
while (isdigit(ch)) X = (X << 3) + (X << 1) + (ch ^ 48), ch = getchar();
return w ? -X : X;
}
inline void write(register int x)
{
if (x < 0) putchar('-'), x = -x;
if (x > 9) write(x / 10);
putchar(x % 10 + '0');
}
int main() {
register int t;
t = read();
while (t--) {
register int n, m;
n = read(), m = read();
memset(G, INF, sizeof(G));
Rep(i, m) {
register int u, v, w;
u = read(), v = read(), w = read();
G[u][v] = w;
}
Rep(i, 6) {
edge[i].x = read(), edge[i].y = read();
}
register int cnt = -1;
while (cnt < 5) {
Rep(k, n) {
Rep(i, n) {
if (i == k || G[i][k] == INF) continue;
Rep(j, n) {
if (G[i][j] > G[i][k] + G[k][j]) {
G[i][j] = G[i][k] + G[k][j];
}
}
}
}
++cnt;
int temp = G[edge[cnt].y][edge[cnt].x];
G[edge[cnt].x][edge[cnt].y] = -temp;
write(-temp);
puts("");
}
}
return 0;
}
【I. Washing clothes】
【题目大意】
有n个人洗衣服,可以手洗也可以使用洗衣机,每个人到达洗衣房的时间为ti,手洗时间为m,可以同时手洗,但洗衣机一次只能洗一个人,问你洗衣机洗衣时间分别为1至m时最后一个人什么时候洗完衣服
【解题思路】
这题十分玄学,正解李超树,但是有人直接根据函数推出了极值点,也有人直接打暴力,反正各种都有,具体的我就不写了,很多博客已经写得很清楚了,以下为几种不同的题解,仅供参考
【1.正解】

【2.推函数】
参考
https://blog.csdn.net/Scar_Halo/article/details/100549332
这里我就不详细展开了,我就就参考博客中自己当时没看明白的地方讲讲
为什么对于g(i) = max(tj + (n - j + 1) * x)
首先考虑将第一位用洗衣机的人编号为1
对于第1个人,如果第二个人的到来时间t2 - t1 > x,那么显然第一个人用洗衣机的时间对答案没有影响,那么就只用考虑从第二个人往后的人对答案的影响
如果t2 - t1 <= x,那么显然第1个人会影响到第2个人用洗衣机,也就是说对答案可能会产生影响,这里那么由于从第一个人往后全用洗衣机,那么对于第一个人,时间显然要往后延迟(n - 1 + 1) * x
该结论可以拓展到用洗衣机的第i个人身上,这里就不展开了,那么该公式显然正确
【3.打暴力】
李超树和推公式都不会,这里考虑直接暴力
既然已经知道对答案有影响的就是第一个手洗的时间超过之后全用洗衣机的人,那么直接暴力枚举找到这个人,然后从这个人开始往后找max就好了
同样由于数据水,以及该函数的极值点特征,暴力不会T
并且实测356ms
【AC代码】
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1000010;
ll a[maxn];
inline ll max(ll a, ll b) { return a > b ? a : b; }
int main() {
ll n, m;
ios::sync_with_stdio(false);
cin.tie(0);
while (cin >> n >> m) {
for (register int i = 1; i <= n; ++i) {
cin >> a[i];
}
sort(a + 1, a + n + 1);
for (register int i = 1; i < m; ++i) {
register ll ans = 0;
register ll j = n - 1;
for (; j >= 1; --j) {
if (m <= i * (n - j + 1)) break;
}
for (register ll k = n; k > j; --k) {
ans = max(ans, a[k] + i * (n - k + 1));
}
if (j) ans = max(ans, a[j] + m); //有可能遍历到开头也没找到(事实上不可能,除非i = m)
cout << ans << " ";
}
cout << a[n] + m << endl;
}
return 0;
}
最后
以上就是高大钢铁侠最近收集整理的关于The Preliminary Contest for ICPC Asia Nanjing 2019 题解的全部内容,更多相关The内容请搜索靠谱客的其他文章。








发表评论 取消回复