快过年了，不准备点窗花都不能说自己学过物理了？！

107 阅读 0 评论 71 点赞

我是靠谱客的博主难过鲜花，最近开发中收集的这篇文章主要介绍快过年了，不准备点窗花都不能说自己学过物理了？！，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

提起这个月的工作重点，

相信大家都会不约而同的说出——

坐等过年！

实不相瞒，

最近小编在实验室…

拧着螺丝想过年，

做着测试想过年，

改着草稿想过年…

虽然距离过年还有一段时间，

但烘托过年氛围的物件已经可以开始准备起来了！

寒冷的冬天，

在表面微微结霜的窗户上贴上精致有趣的窗花，

是小编过年最喜欢的活动之一啦！

古老的民间艺术——窗花

贴在窗户上蕴含着满满年味儿的窗花，承载了上千年的农耕文化，从宋朝、元朝逐渐流传，逐渐成形。

在明清时期，剪纸手工艺术达到了鼎盛时期。清代也有着“剪画聪明胜剪书，飞翔花鸟泳濒鱼。任他二月春风好，剪出垂杨恐不如。”这样的诗句来描绘剪纸艺术。

时至今日，窗花依然寄托着大家的美好愿望，将节日装点得红火富丽、喜气洋洋。

对于剪纸艺术，你知道有哪些技法吗？

剪纸是一种镂空连接的艺术品，按照镂空形式可以分为阴剪（刻）、阳剪（刻）两大类。

阴剪是将图形从纸上剔除，具有“线线相断”的特点；而阳剪是将图形保留，具有“线线相连”的特点。

阴剪和阳剪示意图 | 图片来源：剪纸大图谱

这技法…好像脑子懂了，手却没懂…

很多图案具有对称性的剪纸作品都是通过折剪的方法得到的——将纸张由于纸张以各种不同方式折叠为多层，在折好的纸上进行剪镂。

通过这样的方法，会在折缝上留下连接点，打开来就是一张具有对称性的剪纸作品。

简单的折剪 | 图片来源：剪纸大图谱

除了技法之外，剪纸作品的图案内容也是非常丰富多彩的，通常是吉祥题材剪纸，多为花卉植物、动物飞禽、瓜果虫鱼、山水风景、人物题材和劳动题材。

春耕/胶南剪纸/民间剪纸艺人刘学芳作 | 图片来源：中国乡村剪纸经典

渔业丰收/乐清细纹刻纸 | 图片来源：中国乡村剪纸经典

花篮花儿香/老剪纸 | 图片来源：中国乡村剪纸经典

除此之外，生肖也是剪纸作品的重要题材之一，为了迎接即将到来的虎年，我们一起来看看精美的虎剪纸吧~

虎生肖/老剪纸 | 图片来源：中国生肖剪纸经典

上面这些剪纸作品是不是很生动活泼、精美绝伦？虽然小编不会做剪纸，但我们可以一起从剪纸里挖一挖物理知识。

变了又没变——对称性

对称性是指一个图案能够在经过一种变换操作后能够和原来的图案重合的性质。

我们一起来看看具有对称性的剪纸作品：

图片来源

仔细看看这些图案，我们会很容易的联想到几何对称——轴对称、旋转对称、镜像对称等等。

我们可以将对称分为：反射对称（reflective symmetry）、旋转对称（rotational symmetry）、平移对称（translational symmetry）。除此之外，还有瑕旋转(Improper Rotation)、滑移反射(Glide Reflection)、螺旋旋转(Screw Rotation)这类在两种变换同时进行的条件下保持不变的对称性。

（关于对称类型的详细介绍可以查看往期内容：什么是对称？）

提到物理学中的对称性，最容易想到的就是——晶体。晶体同时具有宏观对称性和微观对称性：宏观对称性就是点对称性，表现在晶体的几何外形上，同时反映在晶体的宏观物理性质中；而微观对称性除了所有宏观对称操作以外，还多了平移对称性，以及由平移和旋转，反映组合成的新对称元素。

（更多有关晶体对称性的知识可以查看往期内容：哈！原来古老的窗花中蕴含着这样的规律？）

对称性不仅是视觉上的，实际上它是内涵更广的概念，可以理解为“变换下的不变性”。将对称性的思想进一步推广，我们可以看到物理定律中蕴含的对称性。在物理学中，一些基础研究都与某些保持不变的物理量或者模式相关。

当我们处于正在运动的列车中，只要列车不进行加速、减速、转弯等活动，列车里的情况给我们的感受与我们在地面是相同的。这之中所蕴含的知识是：两个惯性参考系中的物理规律完全相同，是一种重要的对称性。

诺特定理指出——物理学里的连续对称性和守恒定律一一对应。

质能守恒对应时间平移不变性；动量守恒对应空间平移不变性；角动量守恒对应于旋转不变性。

艺术美、晶体、物理定律等等都在向我们说明着对称性之美，然而，当对称性被打破，我们会得到更加深刻有趣的结果。

对称性破缺与二次谐波

从光学的角度来看，二次谐波（SHG）就是一种与对称性破缺高度相关的现象。

二次谐波是一种二阶非线性光学现象，属于和频非线性效应中的一种。

两个相同频率光子与非线性材料相互作用后合并成一个两倍频率的新光子。

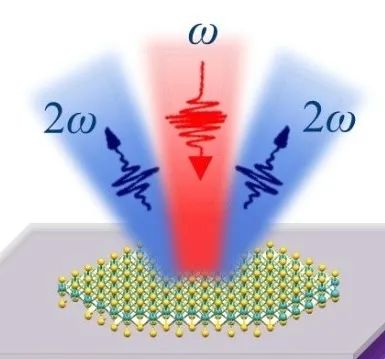
二次谐波示意图 | 图片来源[5]

在应用方面，SHG成像技术被广泛应用于材料科学、多相催化、界面物理化学及生物医学等。

我们在什么情况下才能获得二次谐波呢？

与其他偶数阶非线性光学现象一样，一般我们在具有非中心对称性的化学结构才可以观测到SHG现象。

非线性光学现象广泛的存在于各种不同的介质中，当光场E作用于介质，会产生介质极化强度P。

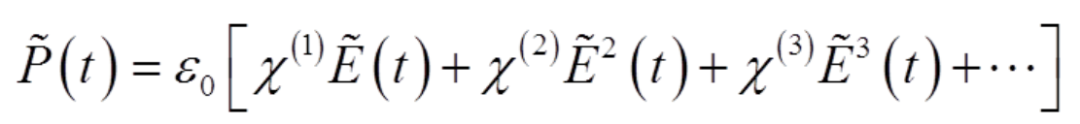
其中，第一项表示线性极化，第二项则对应着二阶非线性光学效应。

在具有中心对称性质的介质中，二阶极化强度之和为零，因此不具有二阶非线性极化。这是对称性破缺在非线性光学领域的一个典型例子。

声波与对称性破缺

除了光与物质相互作用之外，将对称性破缺引入声波也可以带来令人感到惊喜的效果。

伦敦圣保罗大教堂的建筑内有一个奇特的去处——耳语廊，你可以和朋友坐在两面遥遥相对的墙壁旁，对着墙壁悄声对话，虽然看不见对方，却能与对方交流。

图片来源

“耳语廊”模式也被称为“回音壁”模式，由于声波沿着回廊光滑的墙内壁连续反射来进行传播，因而传播损耗很小，这也是对称性在日常生活中很有趣的现象。

基于这种有趣的效应，涌现了大量的研究成果，我们可以通过在器件中人为制造“回音壁”结构，实现声波甚至光波的定向传导。

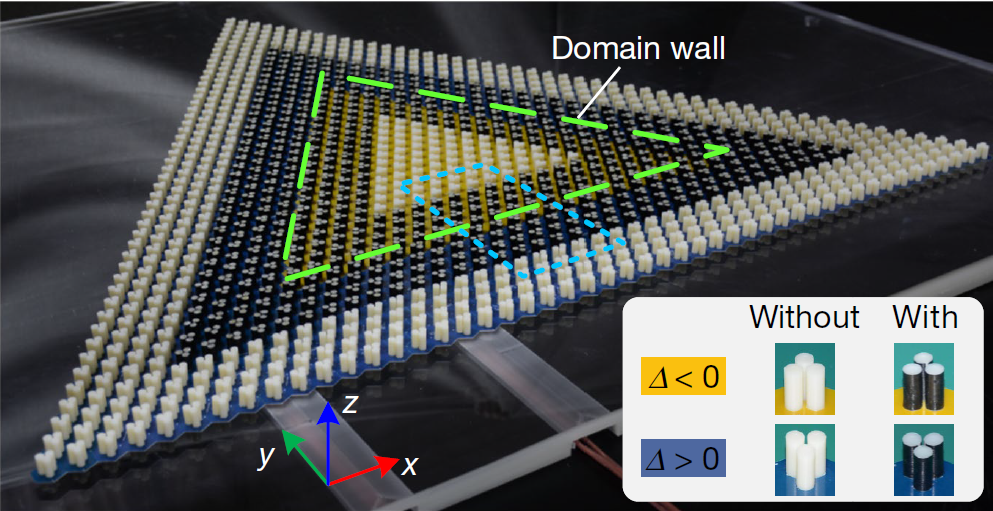
一种人造的“回音壁”结构 | 图片来源[8]

在人造的“回音壁”结构中，可以添加不同的元素来打破声波的对称性：通过打破手性对称性增加增益，允许有选择地放大声波；或者增加拓扑这样的几何布置，打破旋转对称性，允许声波在所需的方向上循环。

这种结构通过引入对称性破缺实现了对声波强度和方向的调控，也具有广泛的应用前景。

对称性破缺与相变

在凝聚态物理领域，朗道将相变与物质结构中对称性的变化相联系。

相变是指物质从一种相转变为另一种相的过程。一级相变是指在发生相变时，物质同时出现体积的变化和热量的吸收或释放。

朗道将从高对称到低对称的相变过程成为“对称破缺”。

另外一个重要的概念是“序参量”，用于反映晶体结构或者电子结构的有序程度。

可能与我们的直觉相反，“对称性”和“有序性”两者是相反的关系。越有序的结构，对称性反而越低。

以水为例，气态水、液态水和冰分别对应水的气、液、固三态，水在这三种状态之间的转变就是相变过程。

冰 | 图片来源：pixabay

水 | 图片来源：pixabay

从对称性来考虑，液相水分子呈无序排列，在每个水分子周围距离相同的位置上，其他原子占据的几率是相同的，因此具有较高的对称性；而固相水分子严格按照周期性排列，其他原子位于某一原子周围的几率是各向异性的，因此相较于液相在结构上对称性较低。

而从有序性来考虑，液态中的水分子做着随机而无规则的布朗运动（Brownian Motion）——没有固定的方向，没有固定的位置，处于完全无序的状态，在任何方向、任何点看起来都是一样的，因此有序性较低；固态中水分子的排列很规则，有序性较高。

根据朗道的理论，从液态水到冰的相变过程就是“对称破缺”而有序性提高的过程。

在发生相变时，体积不变化的情况下，也不伴随热量的吸收和释放，只是热容量、热膨胀系数和等温压缩系数等的物理量发生变化，这一类变化称为二级相变。例如铁磁顺磁相变、零磁场下金属超导态和正常态的转变等。

以铁为例，铁原子具有磁矩，当磁矩排列趋于相同的方向，表现为铁磁性。当我们将温度升高，铁磁性会发生变化，磁矩的方向开始失去规律。当温度升高到某一临界值时，磁矩的排列完全失去了同向性，就全乱了，表现为顺磁性，这一临界温度也被称为居里温度。

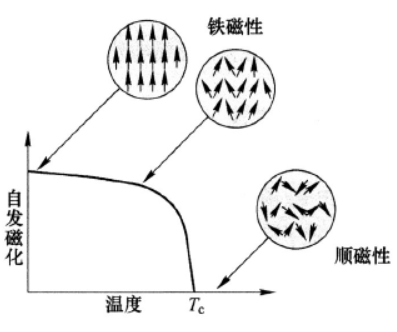
铁磁顺磁相变 | 图片来源

因此，从顺磁到铁磁的相变过程对应着对称性破缺，有序性提升。

朗道相变理论使我们对于各种各样物质状态之间转变的研究更为简洁高效，是凝聚态物理领域重要的基础理论。

两种对称性破缺

对称破缺可以分为：明显对称性破缺（Explicit Symmetry Breaking）和自发对称性破缺（Spontaneous Symmetry Breaking）。

明显性对称破缺源于自然规律，是指对于一些物理系统中不具有物理规律的对称性。

而自发对称性破缺是指物理系统所遵守的自然定律具有某种对称性，而物理系统本身并不具有这种对称性，是一种自发性过程。

如下图所示，假设在墨西哥帽的帽顶有一个圆球，其将处于旋转对称性状态，即围绕帽子中心轴的旋转，圆球的位置不变。

但这种状态是极不稳定的，引入轻微的扰动就会导致圆球掉落——这时帽子仍然具有旋转对称性，而掉落的圆球则导致旋转对称性被打破。

尽管这圆球在帽子谷底的所有可能位置因旋转对称性而相互关联，但实际上，圆球在谷底的位置不具有旋转对称性。这就是一个比较容易理解的自发对称性破缺的例子。

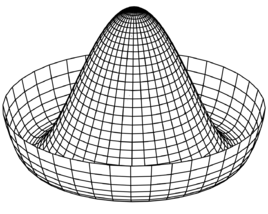
图片来源

我们比较熟悉的BCS理论和希格斯机制都是典型的自发性对称性破缺的例子。更进一步，电磁力和弱相互作用的统一和基本粒子的质量起源问题也由此被解决。

对称性破缺与宇称不守恒

在物理学中，杨振宁、李政道先生在1956年提出的宇称不守恒就与上面提到的明显性对称性破缺相关。

宇称是描述粒子在空间反演下变换性质的相乘性量子数，记为P，只有+1和－1两个值。如果描述某一粒子的波函数在空间反演变换(r→－r)下改变符号，该粒子具有奇宇称(P=－1)，如果波函数在空间反演下保持不变，该粒子具有偶宇称(P=+1)。

宇称不守恒定律，是指在弱相互作用中，互为镜像的物质的运动不对称。

在1956年以前，θ-τ这两种质量和寿命几乎相同，而衰变模式不同的粒子困扰着当时的物理学家们。杨振宁、李政道先生跳出了对称性的思维，转而思考另一种可能性：在弱相互作用中，宇称不守恒。

不久之后，吴健雄先生观测低温下钴60的衰变，为弱相互作用中的宇称不守恒提供了实验证据。

这也是物理学家们在探索自然过程中对称性破缺的思想起到了重要引导作用的著名例子。

读到这里，你还记得我们是怎样一路从窗花讲到这么多的物理知识吗？

有时我们直观感受到很简单的知识和现象，反而能将我们带领到深刻的学术理论中。

对称性破缺的引入确实给我们带来了很有趣且深刻的物理学理论和现象。

那么现在…复杂精美的窗花和深奥优美的物理学知识你掌握了哪个呢？

小编依然感觉…

参考文献：

[1]《剪纸大图谱》

[2]《中国乡村剪纸经典》

[3]《中国生肖剪纸经典》

[4]《中国风·剪纸入门》

[5] https://zhuanlan.zhihu.com/p/165078880

[6]《非线性光学物理》

[7]郭雅文,李源,马宗伟.基于二次谐波产生技术的BaTiO_3薄膜对称性研究[J].光学学报,2021,41(06):191-196.

[8]BolunHu et al, Non-Hermitian topological whispering gallery, Nature (2021).

[9] L.D.Landau，On the theory of phase transitions，1937.

[10]《相变和临界现象》

[11] Nambu,Y.; Jona-Lasinio, G. (April 1961). "DynamicalModel of Elementary ParticlesBased on an Analogy with Superconductivity.I". Physical Review 122:345–358.

[12]宇称不守恒 – 百度

我们是谁：

MatheMagician，中文“数学魔术师”，原指用数学设计魔术的魔术师和数学家。既取其用数学来变魔术的本义，也取像魔术一样玩数学的意思。文章内容涵盖互联网，计算机，统计，算法，NLP等前沿的数学及应用领域；也包括魔术思想，流程鉴赏等魔术内容；以及结合二者的数学魔术分享，还有一些思辨性的谈天说地的随笔。希望你能和我一起，既能感性思考又保持理性思维，享受人生乐趣。欢迎扫码关注和在文末或公众号留言与我交流！