一、RSA算法描述
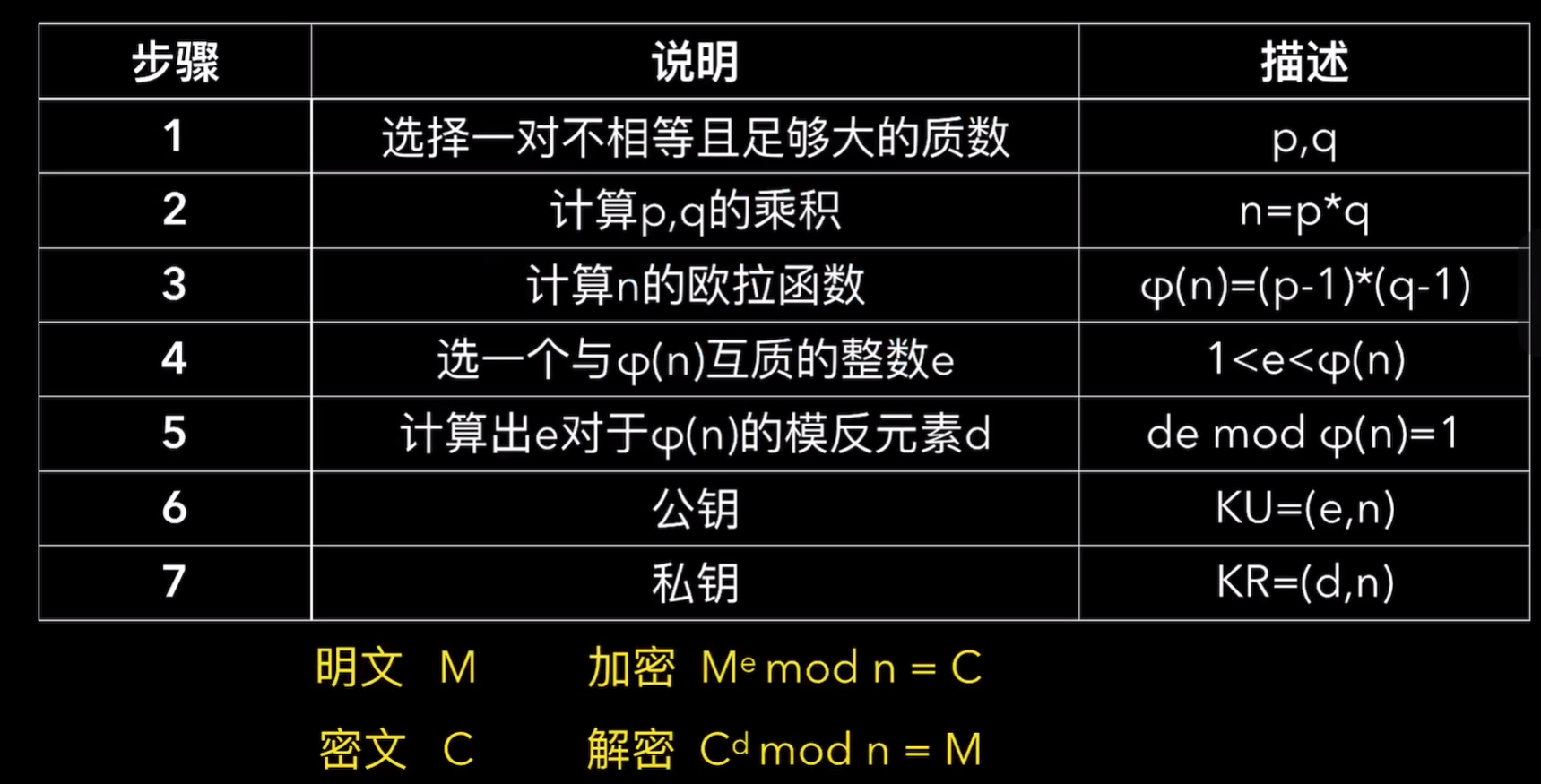
RSA主要利用的是大素数分解的困难性，即知道n如何求出p和q。
二、总体结构
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38//判断是否是素数 public static boolean isPrime(long n) { } //计算欧拉数 public static long Euler(long p, long q) { } //欧几里得算法求两数的最大公因数---a>b static long gcd(long a, long b) { } //求模反元素d（私钥） public static long Key(long e, long euler) { } //递归求n次方 public static long power(long a, long n) { } //加密 public static long encryption(long msg, long e, long n) { } //解密 public static long decryption(long c, long key, long n) { } public static void main(String[] args) { }
三、模块分解
1.判断是否是素数
复制代码
1
2
3
4
5
6
7
8
9
10
11public static boolean isPrime(long n) { boolean b = true; for (long i = 2; i <= Math.sqrt(n); i++) { if (n % i == 0) { b = false; break; } else b = true; } return b; }
2.计算欧拉数
复制代码
1
2
3public static long Euler(long p, long q) { return (p - 1) * (q - 1); }
3.欧几里德算法求两数的最大公因数
复制代码
1
2
3
4
5
6
7
8
9static long gcd(long a, long b) { if (a < b) { long t = a; a = b; b = t; } if (a % b == 0) return b; else return gcd(b, a % b); }
4.求模范元素
复制代码
1
2
3
4
5
6
7public static long Key(long e, long euler) { long key = 1; while ((key * e) % euler != 1) { key++; } return key; }
5.递归求a的n次方
复制代码
1
2
3
4
5
6
7
8public static long power(long a, long n) { long r = 1; if (n == 0) r = 1; else { r = a * power(a, n - 1); } return r; }
6.加密过程
复制代码
1
2
3
4public static long encryption(long msg, long e, long n) { System.out.println("加密中......."); return power(msg, e) % n; }
7.解密过程
复制代码
1
2
3
4public static long decryption(long c, long key, long n) { System.out.println("解密中......."); return power(c, key) % n; }
四、数据结构
long p：大素数p
long q：大素数q
boolean b：判断素数的flag
long euler：p*q的欧拉数
long e：最小的加密密钥e
long key：e对euler的模范元素（即算法描述中的d）
long msg：明文
long c：密文
五、运行结果
这个是选取较小的素数进行测试得到的正确的结果，但是由于long的范围有限，当选取较大的素数进行测试的时候就会因为范围溢出导致数据丢失，从而影响最终的结果，具体如下图所示。
六、源代码
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137package RSA; import java.awt.desktop.SystemEventListener; import java.util.Scanner; public class Demo { //判断是否是素数 public static boolean isPrime(long n) { boolean b = true; for (long i = 2; i <= Math.sqrt(n); i++) { if (n % i == 0) { b = false; break; } else b = true; } return b; } //计算欧拉数 public static long Euler(long p, long q) { return (p - 1) * (q - 1); } //欧几里得算法求两数的最大公因数---a>b static long gcd(long a, long b) { if (a < b) { long t = a; a = b; b = t; } if (a % b == 0) return b; else return gcd(b, a % b); } //求模反元素d（私钥） public static long Key(long e, long euler) { long key = 1; while ((key * e) % euler != 1) { key++; } return key; } //递归求n次方 public static long power(long a, long n) { long r = 1; if (n == 0) r = 1; else { r = a * power(a, n - 1); } return r; } //加密 public static long encryption(long msg, long e, long n) { System.out.println("加密中......."); return power(msg, e) % n; } //解密 public static long decryption(long c, long key, long n) { System.out.println("解密中......."); return power(c, key) % n; } public static void main(String[] args) { System.out.println("--------RSA--------"); //两个大素数 long p; long q; System.out.print("输入两个大素数p、q："); Scanner sc = new Scanner(System.in); p = sc.nextLong(); q = sc.nextLong(); // System.out.println("p = " + p + ",q = " + q); //判断输入的是否是素数 boolean b; //flag //判断p b = isPrime(p); if (b == false) { System.out.println("p = " + p + "不是素数。重新输入p！"); p = sc.nextLong(); b = isPrime(p); while (b = false) { System.out.println("p = " + p + "不是素数。重新输入p！"); p = sc.nextLong(); b = isPrime(p); } } System.out.println(" p = " + p + "是素数。"); //判断q b = isPrime(q); if (b == false) { System.out.println("q = " + q + "不是素数。重新输入q！"); q = sc.nextLong(); b = isPrime(q); while (b = false) { System.out.println("q = " + q + "不是素数。重新输入q！"); q = sc.nextLong(); b = isPrime(q); } } System.out.println(" q = " + q + "是素数。"); //打印最终的p、q System.out.println("p = " + p + ",q = " + q); //计算p、q的欧拉数 long euler = Euler(p, q); System.out.println("Euler(p,q) = " + euler); //选取最小的公钥e，1<e<euler，且与euler互质 long e = 2; while (gcd(e, euler) != 1 || e > euler || e < 1) { e++; } System.out.println("e = " + e); //求出模反元素（私钥） long key = Key(e, euler); System.out.println("key = " + key); //System.out.println(power(2, 2)); //加密过程 System.out.println("输入明文："); long msg = sc.nextLong(); System.out.println("明文：" + msg); long c = encryption(msg, e, p * q);//密文 System.out.println("加密后的密文：" + c); //解密过程 msg = decryption(c, key, p * q); System.out.println("解密后的明文：" + msg); } }
最后
以上就是包容电源最近收集整理的关于RSA算法的Java实现一、RSA算法描述二、总体结构三、模块分解四、数据结构五、运行结果 六、源代码的全部内容，更多相关RSA算法内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
![python 入门学习总结python 入门学习总结[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EU6QwtOg-1658234945849)(C:\Users\luowang\Desktop\2QQ图片20220719200435.png)]](/uploads/reation/bcimg11.png)
发表评论 取消回复