递归算法的优化

/**
 * 递归计算n 的阶乘
 * @param n
 * @return
 */
public long test(long n){

if(n == 1){

return 1;

}else{

return n * test(n-1);

}
}

/**
 * 优化计算 n 的阶乘,尾递归
 * @param n
 * @param result=1
 * @return
 */
public long newTest(long n,long result){

if(n == 1){

return result;

}else{

return newTest(n - 1,n * result);

}
}

分析：上述代码就是递归，通俗的讲就是自己调用自己；
在执行函数test时，他也调用了另外一个函数，只不过这个函数的代码和上一个函数的代码一模一样！是不是很简单 
看一下机器层面的执行过程：
此时就需要引入栈帧的概念了：
1：栈帧将栈分割成N个记录块，每一个记录块的大小是不一样的；
2：这个记录块实际上是编译器用来实现函数调用的数据结构，通俗来讲就是用于活动记录，他用于记录每次函数调用所涉及的相关信息的记录单元；
3：栈帧也是一个函数的执行环境，它包括函数的参数，函数的局部变量函数，执行完之后要返回到哪里等等；

说到这里貌似，大约，好像明白了栈帧原来是用于调用函数的，你每调用一次函数他就会形成一个栈帧用于这个被调用函数的运行环境；
说到这，貌似懂了：上边的test函数在运行时就是形成了一个又一个栈帧啊！

 

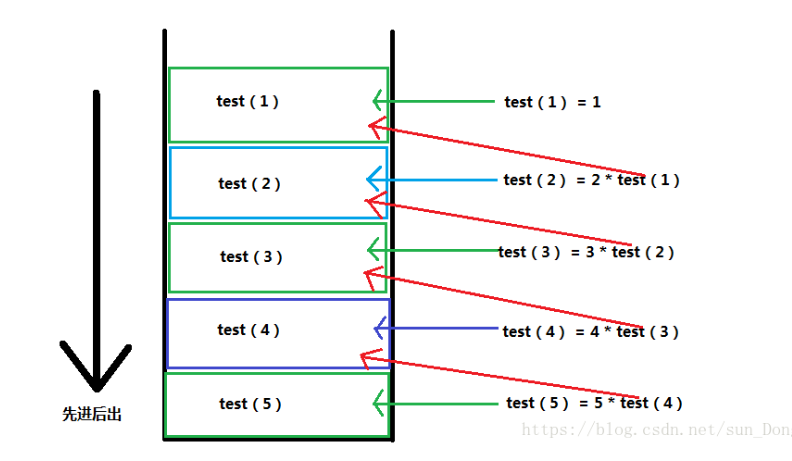
针对上边的递归函数，我画了一幅函数在栈中的执行示意图；
栈是一种先进后出的数据结构！！！
分析：
要求计算5的阶乘；
1）：调用test函数时传入5，即首先在栈中划出一个记录块做为函数test（5）的执行环境；执行到最后结果为： 5 * test（4）；
2）：上一个函数的返回值中调用函数test（4），因此继续指向新的记录块，用于执行函数test（4）；执行到最后结果为： 4 * test（3）；
3）：上一个函数的返回值中调用函数test（3），因此继续指向新的记录块，用于执行函数test（3）；执行到最后结果为： 3 * test（2）；
4）：上一个函数的返回值中调用函数test（2），因此继续指向新的记录块，用于执行函数test（2）；执行到最后结果为： 2 * test（1）；
5）：上一个函数的返回值中调用函数test（1），因此继续指向新的记录块，用于执行函数test（1）；执行到最后test（1）=1；
此时进栈操作已经到达了递归终止的条件，为了计算出最后的test（5）的值需要执行出栈操作；

 

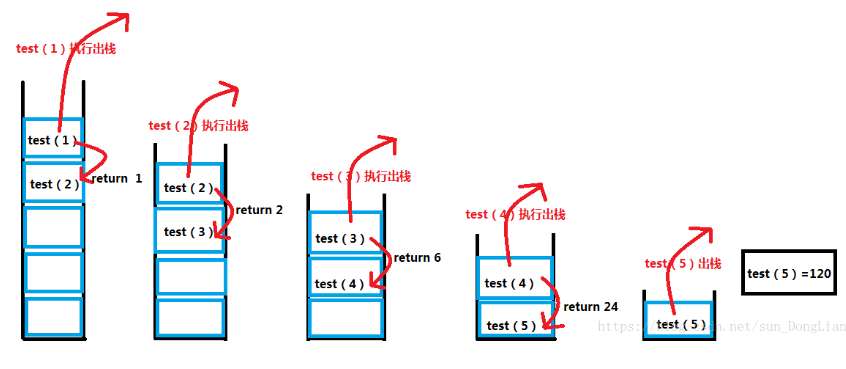
如上图，我画了一幅出栈示意图；栈是先进后出的，所以最后进的要先出。
1）：test（1）出栈，返回值为1；
2）：栈帧test（2）接收test（1）返回值进行计算得出test（2） = 2 * 1 = 2；
3）：test（2）出栈，栈帧test（3）接收test（2）返回值进行计算得出test（3） = 3 * 2 = 6；
4）：test（3）出栈，栈帧test（4）接收test（3）返回值进行计算得出test（4） = 4 * 6 = 24；
5）：test（4）出栈，栈帧test（5）接收test（4）返回值进行计算得出test（5） = 5 * 24 = 120；
6）：test（5）出栈，返回值120，此时表示这一段程序已经执行完毕，计算得出5的阶乘是120；
递归函数写到这一步，貌似是已经完美了，但是你有没有想过：每一个函数test（n） = n * test (n-1)因此每一个栈帧不仅需要保存n值还要记录下一个栈帧的返回值，然后才能计算出来当前栈帧的结果，因此使用多个栈帧是不可避免的，计算5的阶乘就使用了5个栈帧，那要是计算100的呢？10000的呢？。。。。这TM是不是有点始料未及了？栈的大小也是有限的，你就这么用下去，他不给你溢出才怪。

上面的方法实际执行情况

test(10) // 89
test(100) // 堆栈溢出
test()方法100就计算不出来了
newTest(100,1) // 573147844013817200000
newTest(1000,1) // 7.0330367711422765e+208
newTest(10000,1) // Infinity

尾递归优化只在严格模式下生效，那么正常模式下，或者那些不支持该功能的环境中，有没有办法也使用尾递归优化呢？回答是可以的，就是自己实现尾递归优化。

它的原理非常简单。尾递归之所以需要优化，原因是调用栈太多，造成溢出，那么只要减少调用栈，就不会溢出。怎么做可以减少调用栈呢？就是采用“循环”换掉“递归”。

/**
* 循环
* @param n
* @param result=1
* @return
*/
public long doWhell(long n,long result){
while (n>1){
result=result*n;
n--;
}
return
result;
}

综上，递归算法涉及到栈，而栈又是先进后出的原则，因此大量的递归很容易造成栈的内存溢出，因此需要优化。

方向是：递归>>>尾递归>>>循环

所以你不懂递归 还是别玩