Bob has a not even coin, every time he tosses the coin, the probability that the coin's front face up is pq(pq≤21).
The question is, when Bob tosses the coin k times, what's the probability that the frequency of the coin facing up is even number.
If the answer is YX, because the answer could be extremely large, you only need to print (X∗Y−1)mod(109+7).
Input Format
First line an integer T, indicates the number of test cases (T≤100).
Then Each line has 3 integer p,q,k(1≤p,q,k≤107) indicates the i-th test case.
Output Format
For each test case, print an integer in a single line indicates the answer.
样例输入
2 2 1 1 3 1 2
样例输出
500000004 555555560
这题的答案公式很好推,但是怎么化简不好构造;利用了组合数中的二项式展开技巧,因为正面朝上的次数为偶数 所以需要把奇数项消除 构造二项式 令第二项为负数即可消除
思路:
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL mod = 1e9+7;
LL quick(LL x, LL n)
{
LL r=1;
while(n)
{
if(n&1) r=r*x%mod;
n>>=1;
x=x*x%mod;
}
return r%mod;
}
int main()
{
//cout<<quick(2,mod-2)<<endl;
int t;
scanf("%d", &t);
while(t--)
{
LL p, q, k;
scanf("%lld %lld %lld", &p, &q, &k);
LL x=quick(p-2*q,k)*quick(quick(p,k)%mod,mod-2)%mod;
x=(x+1)*quick(2,mod-2)%mod;
printf("%lldn",x);
}
return 0;
}最后
以上就是温柔大象最近收集整理的关于2017 ACM-ICPC 亚洲区(西安赛区)网络赛 Coin(组合数)的全部内容,更多相关2017内容请搜索靠谱客的其他文章。
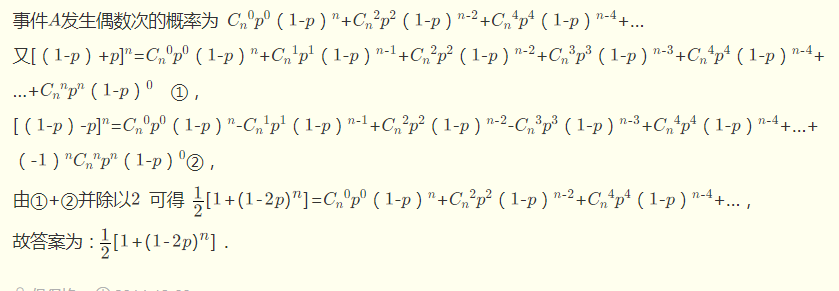








发表评论 取消回复