Finding the Radius for an Inserted Circle 笛卡尔定理 - 2017 ACM-ICPC 亚洲区（南宁赛区）网络赛

96 阅读 0 评论 64 点赞

我是靠谱客的博主冷静板凳，最近开发中收集的这篇文章主要介绍Finding the Radius for an Inserted Circle 笛卡尔定理 - 2017 ACM-ICPC 亚洲区（南宁赛区）网络赛，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

Three circles $C_{a}$ , $C_{b}$ , and $C_{c}$ , all with radius $R$ and tangent to each other, are located in two-dimensional space as shown in Figure $1$ . A smaller circle $C_{1}$ with radius $R_{1}$ ( $R_{1}<R$ ) is then inserted into the blank area bounded by $C_{a}$ , $C_{b}$ , and $C_{c}$ so that $C_{1}$ is tangent to the three outer circles, $C_{a}$ , $C_{b}$ , and $C_{c}$ . Now, we keep inserting a number of smaller and smaller circles $C_{k} (2 leq k leq N)$ with the corresponding radius $R_{k}$ into the blank area bounded by $C_{a}$ , $C_{c}$ and $C_{k-1}$ $(2 \leq k \leq N)$ , so that every time when the insertion occurs, the inserted circle $C_{k}$ is always tangent to the three outer circles $C_{a}$ , $C_{c}$ and $C_{k-1}$ , as shown in Figure $1$

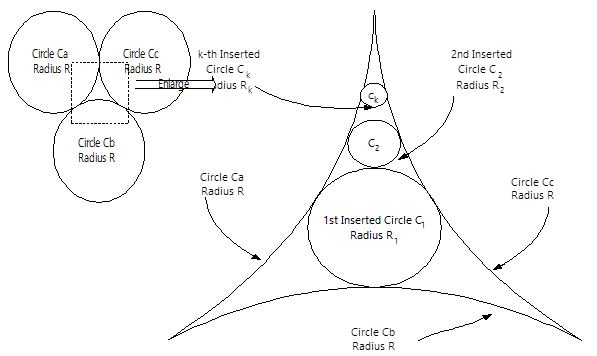
Figure 1.

(Left) Inserting a smaller circle $C_{1}$ into a blank area bounded by the circle $C_{a}$ , $C_{b}$ and $C_{c}$ .

(Right) An enlarged view of inserting a smaller and smaller circle $C_{k}$ into a blank area bounded by $C_{a}$ , $C_{c}$ and $C_{k-1}$ ( $2 \leq k \leq N$ ), so that the inserted circle $C_{k}$ is always tangent to the three outer circles, $C_{a}$ , $C_{c}$ , and $C_{k-1}$ .

Now, given the parameters $R$ and $k$ , please write a program to calculate the value of $R_{k}$ , i.e., the radius of the $k - t h$ inserted circle. Please note that since the value of $R_k$ may not be an integer, you only need to report the integer part of $R_{k}$ . For example, if you find that $R_{k}$ = $1259.8998$ for some $k$ , then the answer you should report is $1259$ .

Another example, if $R_{k}$ = $39.1029$ for some $k$ , then the answer you should report is $39$ .

Assume that the total number of the inserted circles is no more than $10$ , i.e., $N \leq 10$ . Furthermore, you may assume $π = 3.14159$ . The range of each parameter is as below:

$1 \leq k \leq N$ , and $10^{4} leq R leq 10^{7}$ .

Input Format

Contains $l + 3$ lines.

Line $1$ : $l$ ----------------- the number of test cases, $l$ is an integer.

Line $2$ : $R$ ---------------- $R$ is a an integer followed by a decimal point,then followed by a digit.

Line $3$ : $k$ ---------------- test case # $1$ , $k$ is an integer.

$\dots$

Line $i + 2$ : $k$ ----------------- test case # $i$ .

$\dots$

Line $l + 2$ : $k$ ------------ test case # $l$ .

Line $l + 3$ : $- 1$ ---------- a constant $- 1$ representing the end of the input file.

Output Format

Contains $l$ lines.

Line $1$ : $k$ $R_{k}$ ----------------output for the value of $k$ and $R_{k}$ at the test case # $1$ , each of which should be separated by a blank.

$\dots$

Line $i$ : $k$ $R_{k}$ ----------------output for $k$ and the value of $R_{k}$ at the test case # $i$ , each of which should be separated by a blank.

Line $l$ : $k$ $R_{k}$ ----------------output for $k$ and the value of $R_{k}$ at the test case # $l$ , each of which should be separated by a blank.

样例输入

样例输出

1 23665

题目来源

2017 ACM-ICPC 亚洲区（南宁赛区）网络赛

题目如图所示，给出开始时圆的半径，求构造出的第k个圆的半径。

笛卡尔定理如下：

定义一个圆的曲率 k=±1r ，其中 r 是其半径。
若平面有两两相切，且有 6 个独立切点的四个圆，设其曲率为 k1,k2,k3,k4 （若该圆与其他圆均外切，则曲率取正，否则取负）则其满足性质：

(k 1 + k 2 + k 3 + k 4) 2 = 2 (k 21 + k 22 + k 23 + k 24)

接着，套公式算就可以了。

#include <cstdio>
#include <iostream>
#include <string.h>
#include <string>
#include <map>
#include <queue>
#include <vector>
#include <set>
#include <algorithm>
#include <math.h>
#include <cmath>
#include <stack>
#include <iomanip>
#define mem0(a) memset(a,0,sizeof(a))
#define meminf(a) memset(a,0x3f,sizeof(a))
using namespace std;
typedef long long ll;
typedef long double ld;
typedef double db;
const int maxn=100005, inf = 0x3f3f3f3f;
const ll llinf = 0x3f3f3f3f3f3f3f3f;
const ld pi = 3.14159L;
ld ans[15];
int main() {
int cnt = 0,sum=0;
ld l = 0L,r;
int cas,s,i,k;
scanf("%d", &cas);
cin >> r;
l = 1.0L / r ;
r = l;
for (i = 1; i <= 10; i++) {
ans[i] = sqrt(2.0L*((r+r+l)*(r+r+l)-r*r-r*r - l*l));
ans[i] += r + r + l;
//	cout << ans[i] << endl;
l = ans[i];
ans[i] = 1.0L / ans[i];
}
while (cas--) {
scanf("%d", &k);
s = floor(ans[k]);
printf("%d ", k);
cout << s << endl;
}
//
system("pause");
return 0;
}