Recently, Pari and Arya did some research about NP-Hard problems and they found theminimum vertex cover problem very interesting.
Suppose the graph G is given. Subset A of its vertices is called a vertex cover of this graph, if for each edgeuv there is at least one endpoint of it in this set, i.e.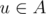 or
or (or both).
(or both).
Pari and Arya have won a great undirected graph as an award in a team contest. Now they have to split it in two parts, but both of them want their parts of the graph to be a vertex cover.
They have agreed to give you their graph and you need to find two disjoint subsets of its vertices A andB, such that both A andB are vertex cover or claim it's impossible. Each vertex should be given to no more than one of the friends (or you can even keep it for yourself).
The first line of the input contains two integers n andm (2 ≤ n ≤ 100 000,1 ≤ m ≤ 100 000) — the number of vertices and the number of edges in the prize graph, respectively.
Each of the next m lines contains a pair of integersui andvi (1 ≤ ui, vi ≤ n), denoting an undirected edge between ui andvi. It's guaranteed the graph won't contain any self-loops or multiple edges.
If it's impossible to split the graph between Pari and Arya as they expect, print "-1" (without quotes).
If there are two disjoint sets of vertices, such that both sets are vertex cover, print their descriptions. Each description must contain two lines. The first line contains a single integerk denoting the number of vertices in that vertex cover, and the second line containsk integers — the indices of vertices. Note that because ofm ≥ 1, vertex cover cannot be empty.
4 2 1 2 2 3
1 2 2 1 3
3 3 1 2 2 3 1 3
-1
In the first sample, you can give the vertex number 2 to Arya and vertices numbered1 and 3 to Pari and keep vertex number4 for yourself (or give it someone, if you wish).
In the second sample, there is no way to satisfy both Pari and Arya.
题意:给你一些顶点和边,让你把他们分成两个组,并且同组内顶点不能有边连接
思路:直接二分图,dfs/bfs来判断,首先分成两组嘛,那就是给这两组进行染色,如果出息你属于同一组的那么一定不是二分图,然后一组染色为1,另一组染色为2进行判断
DFS写法:
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <stack>
using namespace std;
int vist[100030],flag,val[100030],n,m;
vector <int>v[100030];
void dfs(int i,int va) {
vist[i] = 1;
val[i] = va;
for(int j = 0; j < (int)v[i].size(); j++) {
if(!vist[v[i][j]]) {
dfs(v[i][j],3-va);
} else if(val[v[i][j]] == va) {
flag = 1;
return;
}
}
}
int main() {
cin >> n >> m;
memset(vist,0,sizeof(vist));
memset(val,-1,sizeof(val));
while(m--) {
int x,y;
cin >> x >> y;
v[x].push_back(y);
v[y].push_back(x);
}
flag = 0;
for(int i = 1;i<= n;i++){
if(val[i] == -1){
dfs(i,1);
}
if(flag){
break;
}
}
if(flag == 1) {
cout << "-1" <<endl;
} else {
int tot = 0;
for(int i = 1; i <= n; i++) {
if(val[i] == 1) {
tot++;
}
}
cout << tot << endl;
for(int i = 1; i <= n; i++) {
if(val[i] == 1) {
cout << i << " ";
}
}
tot = 0;
for(int i = 1; i <= n; i++) {
if(val[i] == 2) {
tot++;
}
}
cout <<endl <<
tot << endl;
for(int i = 1; i <= n; i++) {
if(val[i] == 2) {
cout << i << " ";
}
}
cout << endl;
}
return 0;
}
BFS写法
#include<iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include <cstring>
using namespace std;
int color[100030];
vector < int > mp[100030];
int n,m;
int bfs(int ss) {
color[ss] = 1;
queue<int>s;
s.push(ss);
while(!s.empty()) {
int u = s.front();
s.pop();
int len=mp[u].size();
for(int i = 0; i < len; i++) {
int v = mp[u][i];
if(u == v)continue;
if(color[v] == -1) {
color[v] = 3-color[u];
s.push(v);
} else {
if(color[u] == color[v]) {
return 0;
}
}
}
}
return 1;
}
int main() {
cin >> n >> m;
memset(color,-1,sizeof(color));
for(int i = 0;i < m;i++){
int x,y;
cin >> x >> y;
mp[x].push_back(y);
mp[y].push_back(x);
}
int tt = 1;
for(int i = 1;i<= n;i++){
if(color[i] == -1){
int ttt = bfs(i);
if(ttt == 0){
tt = 0;
break;
}
}
}
if(tt == 0){
cout << "-1" << endl;
}else{
int tot = 0;
for(int i = 1;i <= n;i++){
if(color[i] == 1){
tot++;
}
}
cout << tot << endl;
for(int i = 1;i <= n;i++){
if(color[i] == 1){
cout << i << " ";
}
}
tot = 0;
for(int i = 1;i <= n;i++){
if(color[i] == 2){
tot++;
}
}
cout <<endl <<
tot << endl;
for(int i = 1;i <= n;i++){
if(color[i] == 2){
cout << i << " ";
}
}
cout << endl;
}
return 0;
}
最后
以上就是舒服金针菇最近收集整理的关于codeforces 688c 二分图判断的全部内容,更多相关codeforces内容请搜索靠谱客的其他文章。








发表评论 取消回复