文章目录
- 我加的概念
- 积和式模2和行列式
- 积和式模2^k
- Permanent:偶图(二部图)的带权完美匹配数目
- 行列式:带符号的图覆盖于带符号的偶图完美匹配
- Pfaffian:带符号的完美匹配
- 反对称矩阵的Pfaffian
- 一般图的pfaffian$le_T$平面图的完美匹配
- 匹配门
- 用平面图模拟一般图
- 匹配门等式
- 用封闭性证明
- Juxtaposition
- jumper
我加的概念
- 匹配:边集,任两边无公共vertex。
- 最大:含边数最多的匹配。
- 完美:若一个图的某匹配,所有点都是匹配点。
- 完美定是最大,并非每个图都有完美。
积和式模2和行列式
- D e s ( A ) = ∣ A ∣ = ∑ π ∈ S n ( − 1 ) ϵ ( π ) ∏ j = 1 n A j , π ( j ) Des(A)=|A|=sum_{piin S_n}(-1)^{epsilon(pi)}prod_{j=1}^{n}A_{j,pi(j)} Des(A)=∣A∣=π∈Sn∑(−1)ϵ(π)j=1∏nAj,π(j)
- poly可计算
- P e r m a n e n t ( A ) = ∣ A ∣ = ∑ π ∈ S n ∏ j = 1 n A j , π ( j ) Permanent(A)=|A|=sum_{piin S_n}prod_{j=1}^{n}A_{j,pi(j)} Permanent(A)=∣A∣=π∈Sn∑j=1∏nAj,π(j)
- 同奇偶
积和式模2^k
Permanent:偶图(二部图)的带权完美匹配数目
- P e r m a n e n t ( A ) = ∣ A ∣ = ∑ π ∈ S n ∏ j = 1 n A j , π ( j ) Permanent(A)=|A|=sum_{piin S_n}prod_{j=1}^{n}A_{j,pi(j)} Permanent(A)=∣A∣=π∈Sn∑j=1∏nAj,π(j)
- n n n个点的有向图, 2 n 2n 2n个点的偶图
- 有向中,有向边的权重
W
(
j
,
k
)
=
A
j
,
k
W(j,k)=A_{j,k}
W(j,k)=Aj,k
- Permanent(A)是有向图的什么呢?Cyclecover呀!
- 置换可以分解为轮换的乘积,轮换就对应一个圈啊。
- 无向偶中,边
W
(
j
,
k
′
)
=
A
j
,
k
W(j,k')=A_{j,k}
W(j,k′)=Aj,k
- Permanent(A)是无向偶图的什么呢?
- 对应这个矩阵 ( O A A ′ O ) left(begin{array}{cc} O&A\ A'&O end{array}right) (OA′AO)完美匹配哦
行列式:带符号的图覆盖于带符号的偶图完美匹配
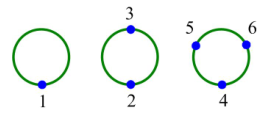
- π = ( 1 ) ( 23 ) ( 456 ) = ( 123456 1 ′ 3 ′ 2 ′ 5 ′ 6 ′ 4 ′ ) pi=(1)(23)(456)=left( begin{array}{cc} 123456\ 1'3'2'5'6'4'\ end{array} right) π=(1)(23)(456)=(1234561′3′2′5′6′4′)
- 圈覆盖怎么看符号?
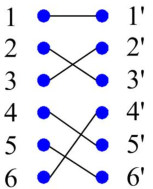
- 偶图完美匹配怎么看符号?
Pfaffian:带符号的完美匹配
- G G G是边权重的, 2 n 2n 2n点的无向图
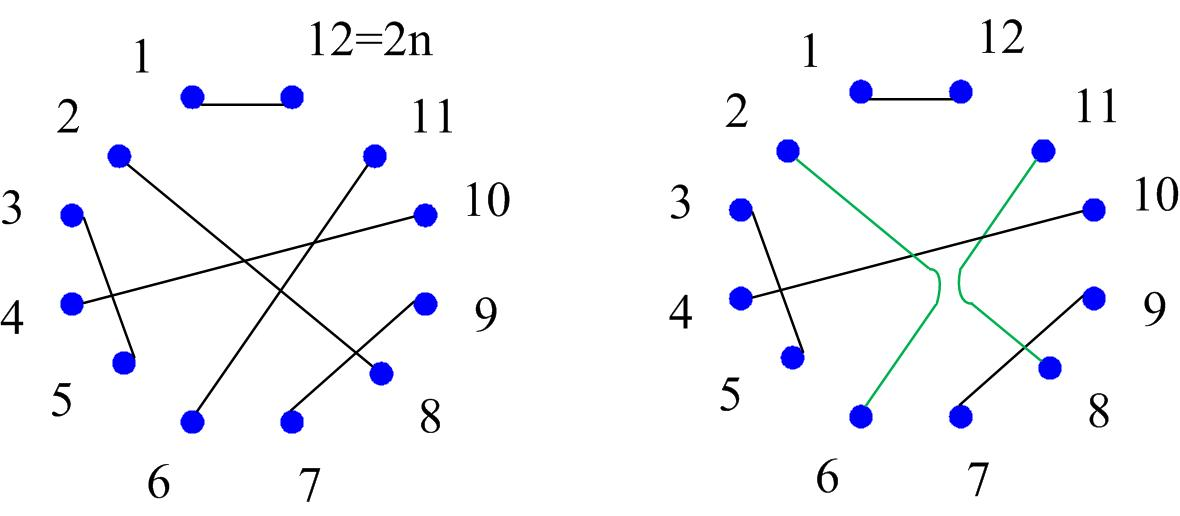
- P f a f f i a n ( G ) = ∑ M 是 G 的 完 配 ( − 1 ) M 交 叉 数 ( M 权 重 ) Pfaffian(G)=sum_{M是G的完配}(-1)^{M交叉数}(M权重) Pfaffian(G)=M是G的完配∑(−1)M交叉数(M权重)
- 交换匹配中两个边的匹配对象,交叉数目变1。
- 还有一个规则,太简单了,就是将7个9交换,然后奇偶性不变,这谁看不出来?
反对称矩阵的Pfaffian
- M j , k = − M k , j M_{j,k}=-M_{k,j} Mj,k=−Mk,j
- 奇数大小的反对称矩阵的 P f a f f i a n = 0 Pfaffian=0 Pfaffian=0
- 如果是偶数
2
n
2n
2n
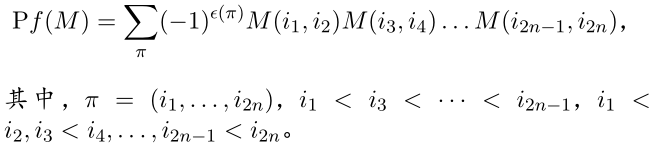
- Pfaffian有类似高斯消元算法
- P f ( A ) 2 = D e t ( A ) Pf(A)^2=Det(A) Pf(A)2=Det(A)
一般图的pfaffian ≤ T le_T ≤T平面图的完美匹配
- 下面这个图的完美匹配是3,带符号的话应该是1+1-1=1,这就是pfaffian,如何将这个归约到平面图的不带符号的完美匹配呢?
- 需要模拟交叉。
- 我们只需要保证插入的 C C C函数在4个地方上有数值,其他为零就ok,想想为什么?
- 注意4个值里面需要有-1去模拟交叉
- 具体是啥见下一页哦
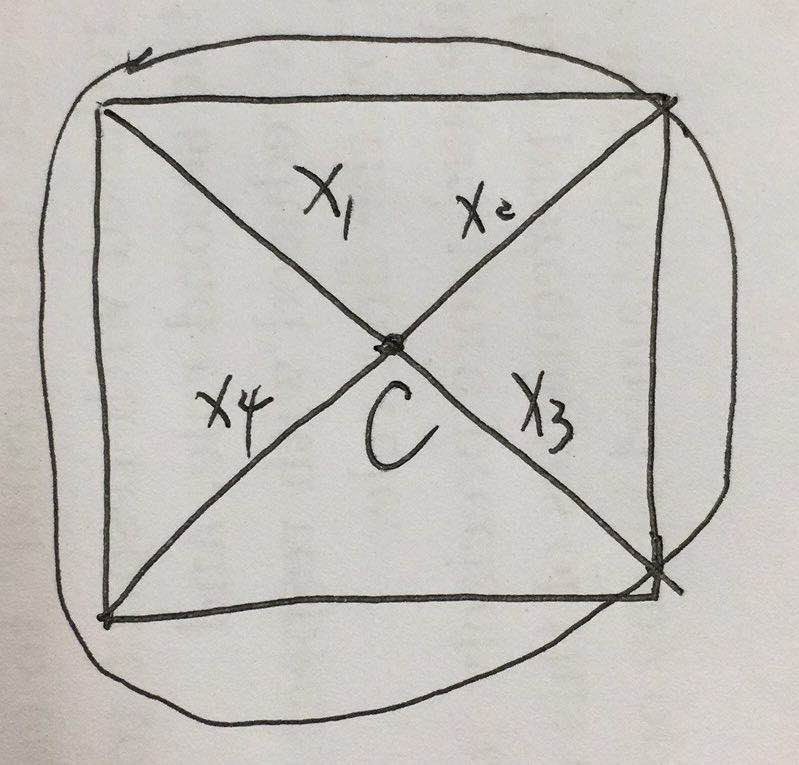
匹配门
-
完美匹配就是 [ 0 , 1 , 0 , . . . 0 ] [0,1,0,...0] [0,1,0,...0]构成的张量网络
-
权重 w w w的边,是在边的中点加上 [ 1 , 0 , w ] [1,0,w] [1,0,w]
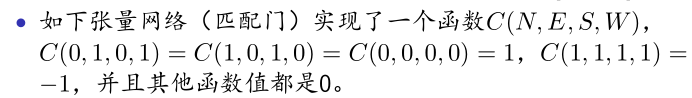
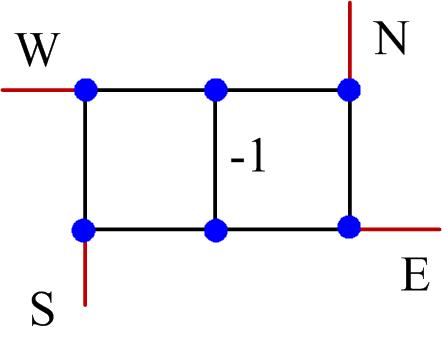
-
不信你可以算一下,过程如下。
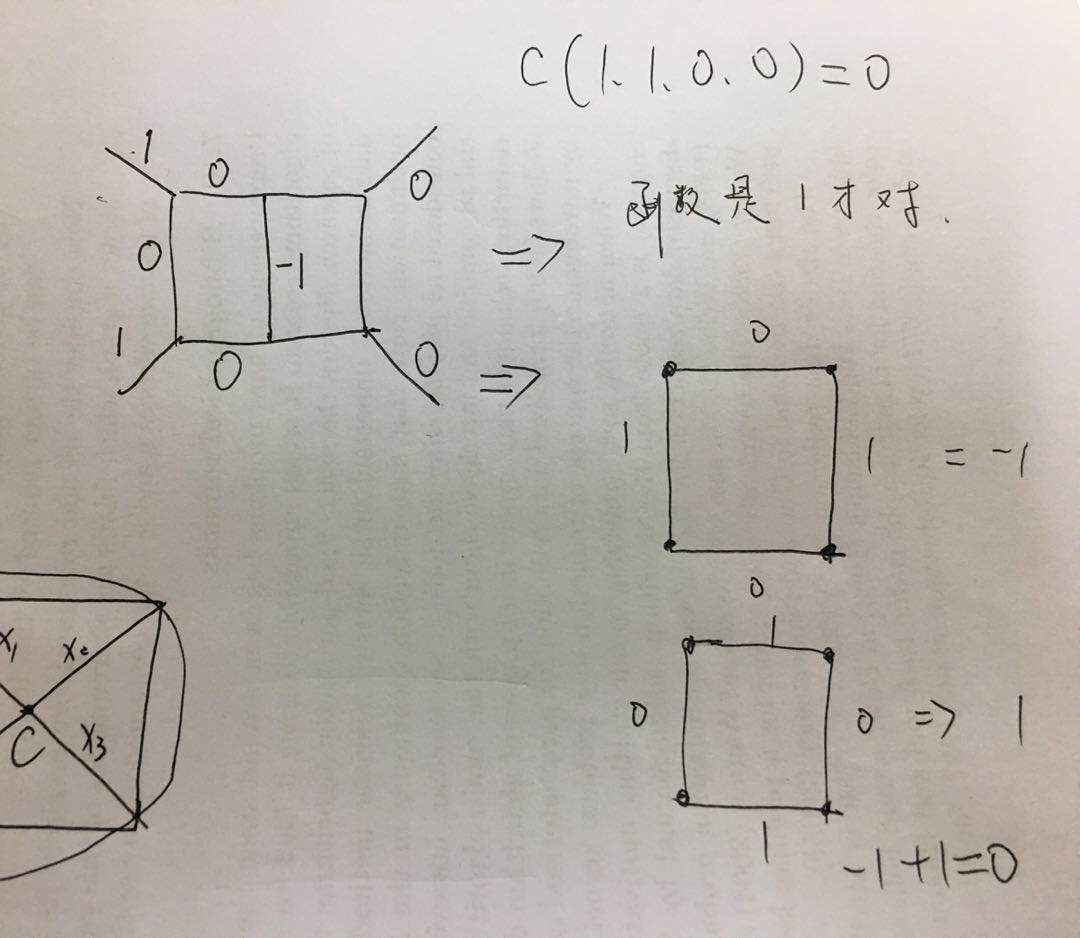
-
实际已经归约了完成了。
用平面图模拟一般图
- 第四点实际上是实现不了的,

匹配门等式
- 一个 # p l a n a r P M #planarPM #planarPM生成的张量网络一定满足下面函数
- e p j 是 单 位 向 量 , e_{p_j}是单位向量, epj是单位向量,只在 p j p_j pj位置是1

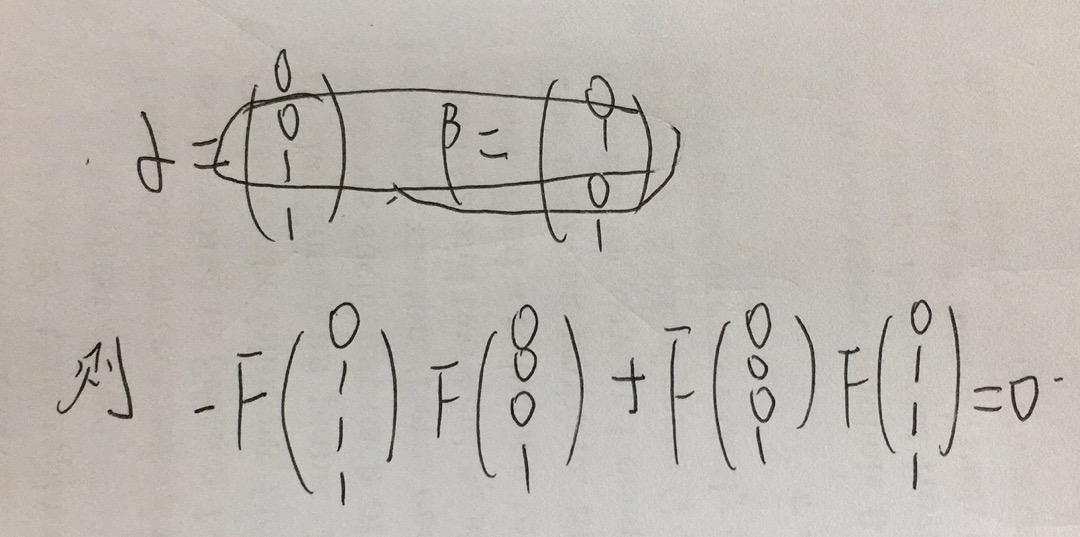
用封闭性证明
- 第一个是说如果 P P P和 Q Q Q是满足等式,那么俩乘积也是的
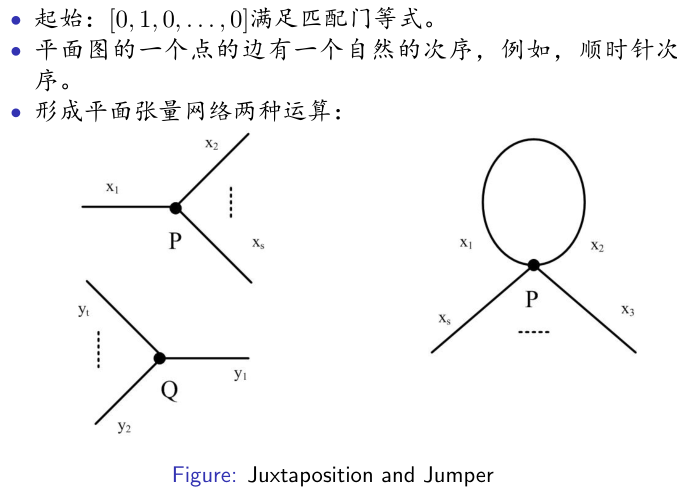
Juxtaposition
- 如果 P P P满足, Q Q Q满足,那么俩个乘积记为 F F F
-
I
(
F
,
α
,
β
)
I(F,alpha,beta)
I(F,α,β)表示作用在哪个函数啊
- 那么
I
(
P
,
α
,
β
)
=
0
I(P,alpha,beta)=0
I(P,α,β)=0,
I
(
Q
,
α
′
,
β
′
)
=
0
I(Q,alpha',beta')=0
I(Q,α′,β′)=0
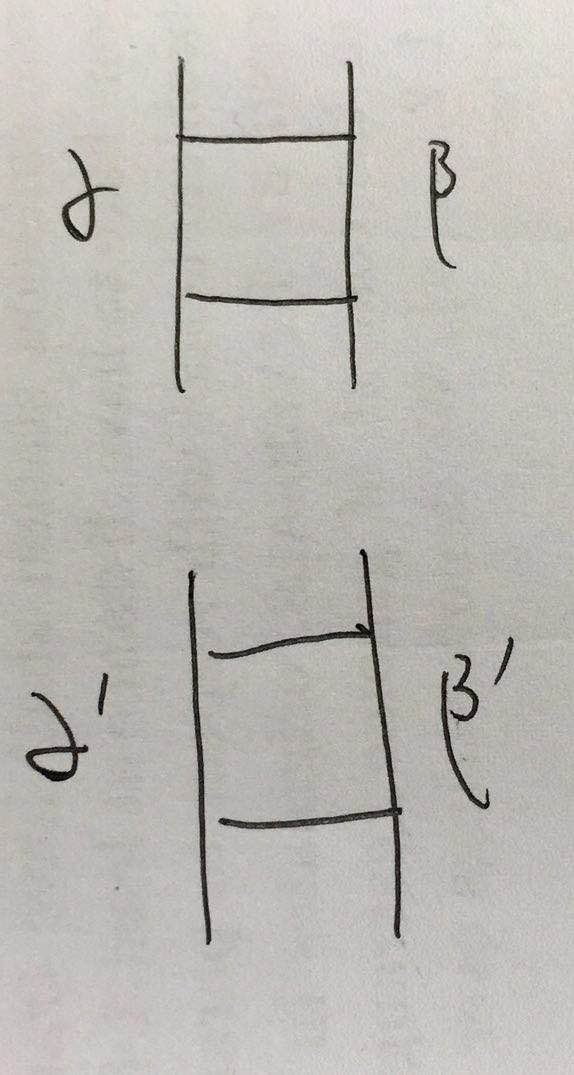
- 那么
I
(
P
,
α
,
β
)
=
0
I(P,alpha,beta)=0
I(P,α,β)=0,
I
(
Q
,
α
′
,
β
′
)
=
0
I(Q,alpha',beta')=0
I(Q,α′,β′)=0
- 结合上面的图,你就知道了为什么 I ( F , α α ′ , β β ′ ) I(F,alphaalpha',betabeta') I(F,αα′,ββ′)等于什么了
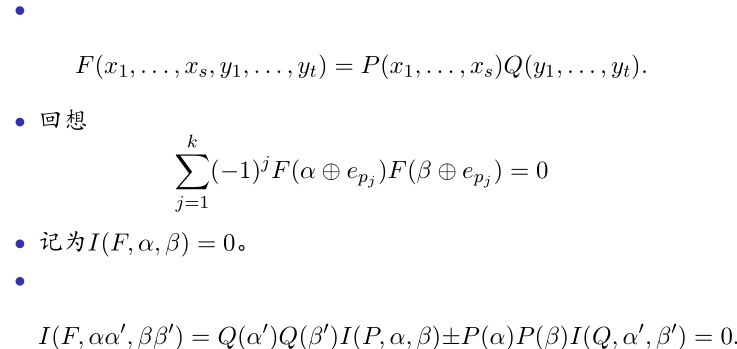
jumper
最后
以上就是拼搏人生最近收集整理的关于完美匹配我加的概念积和式模2和行列式积和式模2^kPermanent:偶图(二部图)的带权完美匹配数目行列式:带符号的图覆盖于带符号的偶图完美匹配Pfaffian:带符号的完美匹配反对称矩阵的Pfaffian一般图的pfaffian ≤ T \le_T 的全部内容,更多相关完美匹配我加的概念积和式模2和行列式积和式模2^kPermanent:偶图(二部图)的带权完美匹配数目行列式:带符号的图覆盖于带符号的偶图完美匹配Pfaffian:带符号的完美匹配反对称矩阵的Pfaffian一般图的pfaffian 内容请搜索靠谱客的其他文章。








发表评论 取消回复