leetcode 120. 三角形最小路径和递归—超时版本记忆化递归自上而下的动态规划自下而上的动态规划动态规划空间优化

131 阅读 0 评论 87 点赞

我是靠谱客的博主欢呼羽毛，这篇文章主要介绍leetcode 120. 三角形最小路径和递归—超时版本记忆化递归自上而下的动态规划自下而上的动态规划动态规划空间优化，现在分享给大家，希望可以做个参考。

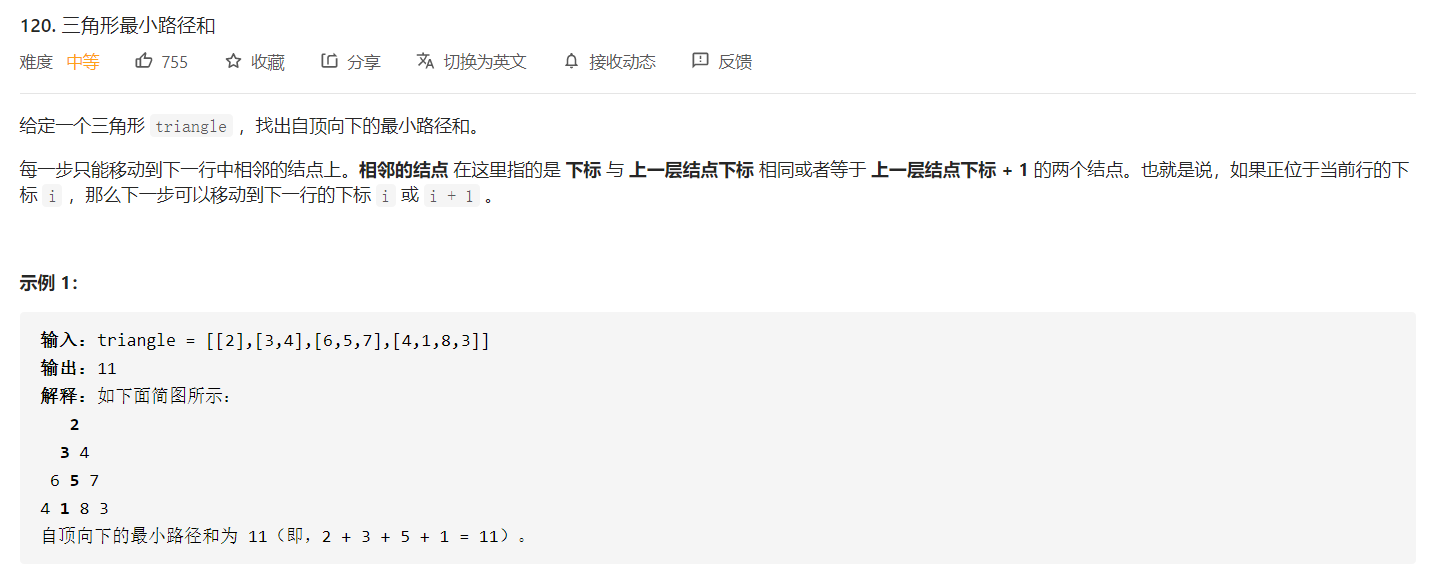
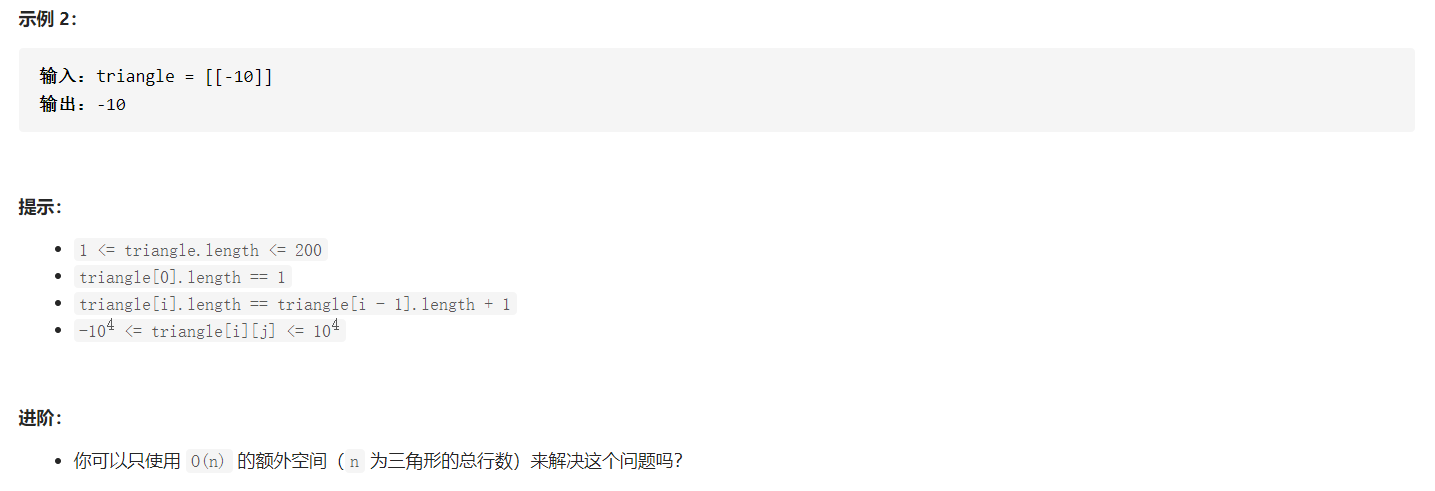
在这里插入图片描述

三角形最小路径和题解整理

递归---超时版本
记忆化递归
自上而下的动态规划
自下而上的动态规划
动态规划空间优化

递归—超时版本

分析：

复制代码

1
2
3
4
5
6
7
8
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
相邻结点：与(i, j) 点相邻的结点为 (i + 1, j) 和 (i + 1, j + 1)。

若定义 f(i, j) 为 (i, j) 点到底边的最小路径和，则易知递归求解式为:
f(i, j) = min(f(i + 1, j), f(i + 1, j + 1)) + triangle[i][j]
由此，我们将任一点到底边的最小路径和，转化成了与该点相邻两点到底边的最小路径和中的较小值，再加上该点本身的值。这样本题的递归解法就完成了。

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
	int minimumTotal(vector<vector<int>>& triangle) {
		return dfs(triangle, 0, 0);
	}
	int dfs(vector<vector<int>>& triangle,int i,int j)
	{
		if (i == triangle.size()) return 0;
		return min(dfs(triangle, i + 1, j),dfs(triangle,i+1,j+1))+triangle[i][j];
	}
};

在这里插入图片描述

记忆化递归

通过一个map容器记录保存计算出来的结果.下一次如果用到了直接返回，不需要再次递归计算

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
	map<pair<int, int>, int> map;
public:
	int minimumTotal(vector<vector<int>>& triangle) {
		return dfs(triangle, 0, 0);
	}
	int dfs(vector<vector<int>>& triangle,int i,int j)
	{
		if (i == triangle.size()) return 0;
		if (map.find({ i,j }) != map.end()) return map[{i, j}];
		return map[{i, j}]=min(dfs(triangle, i + 1, j), dfs(triangle, i + 1, j + 1))+triangle[i][j];
	}
};

在这里插入图片描述

自上而下的动态规划

题目给出的例子看上去不是那么直观，现在我们把例子中的数组位置重新摆放一下。那么自顶向下的移动路线就是这样的
也就是triangle[i][j]可以向triangle[i+1][j]移动，也可以向triangle[i+1][j+1]移动
这个三角形的最小路径和就是2->3->5->1，
我们用一个dp数组保存每次移动的最小值，2->3->5->1这个路径移动后在dp数组中保存的结果就是2->5->10->11
反过来说，对于三角形中任意一个位置triangle[i][j]，只有两个值能移动到这个位置
分别是triangle[i-1][j-1]，以及triangle[i-1][j]，如下图所示
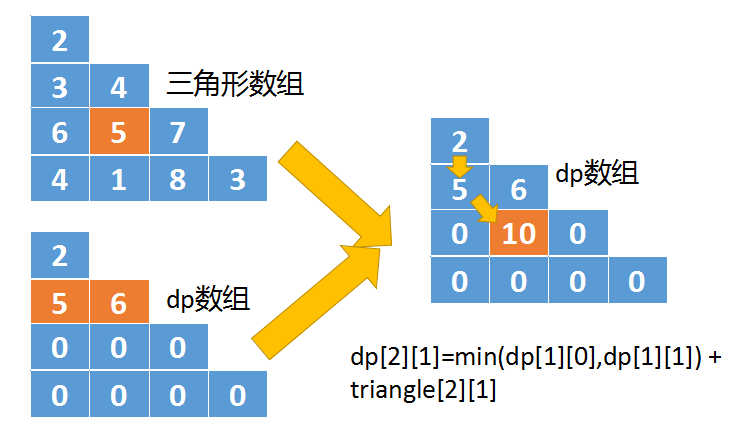
对于triangle[2][1]这个位置，它是从triangle[1][0]，以及triangle[1][1]这两个位置移动而来的。而这两个值我们已经先保存到dp[1][0]和dp[1][1]中了。
我们从dp[1][1]和dp[1][0]中选择一个较小的值，这里就是5，然后再加上triangle[2][1]的值5，将结果10保存到dp[2][1]中。
dp转移公式为：
dp[i][j] = min(dp[i-1][j-1],dp[i-1][j])+triangle[i][j]
使用上面那个转移公式，这题基本上就可以搞定了
但需要注意的是，自上而下推导时，有两个特例
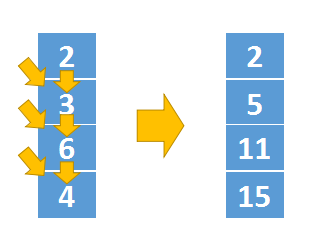
第一列计算的时候，如果用dp[i-1][j-1]获取斜上方值时会出现下标越界。从上图中我们也可以发现，实际上第一列计算的时候，它只有一条转移路径，我们需要单独处理，其计算公式如下，
dp[i][0] = dp[i-1][0] + triangle[i][0]
第二个特例是三角形的斜边
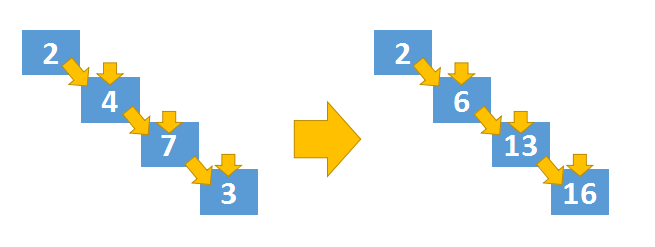
通过上图我们可以发现，这条斜边也是只有一条转移路径，同样也需要单独处理，其计算公式如下:
dp[i][j] = dp[i-1][j-1] + triangle[i][j]
自上而下推到到最后一行就结束了，但最后一行的哪一列是最终值我们并不知道，因为很多条转移路径都会到达最后一行。所以动态规划整个计算过程结束后，我们还需要再计算一下最后一行的min值，这个min值就是最终的结果。
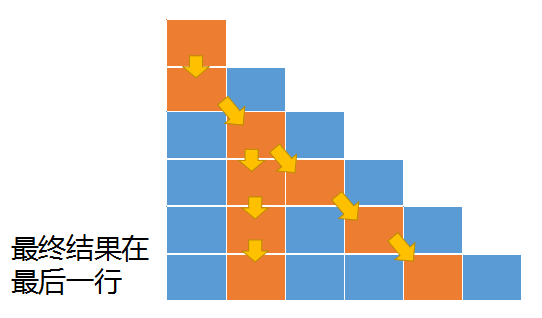
时间复杂度:O(N^2)
空间复杂度:O(N^2)

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
	int minimumTotal(vector<vector<int>>& triangle) 
	{
		if (triangle.empty()) return 0;
		int r = triangle.size();//行
		vector<vector<int>> dp(triangle.size(), vector<int>(triangle[r-1].size()));
		//初始值
		dp[0][0] = triangle[0][0];
		//第一列
		for (int i = 1; i < r; i++)
			dp[i][0] = dp[i - 1][0] + triangle[i][0];
		for (int i = 1; i < r; ++i)
		{
			int j = 1;
			//注意计算的是三角形每一行的长度都不同
            //最后一列需要单独计算(斜边)，所以是从遍历的个数是size()-1
			while (j <triangle[i].size()-1)
			{
				//状态转移公式
				dp[i][j] = min(dp[i - 1][j - 1], dp[i-1][j])+triangle[i][j];
				++j;
			}
			//三角形斜边需要单独计算
			dp[i][j] = dp[i - 1][j - 1] + triangle[i][j];
		}
		//最后一行保存了每条路径的计算结果，对最后一行数组求min即为最终结果
		     int Min = INT_MAX;
			for (int j = 0; j <triangle[r-1].size(); j++)
			{
				Min = min(Min, dp[r-1][j]);
			}
			return Min;
	}
};

在这里插入图片描述

自下而上的动态规划

下图演示的是自下而上的推导过程
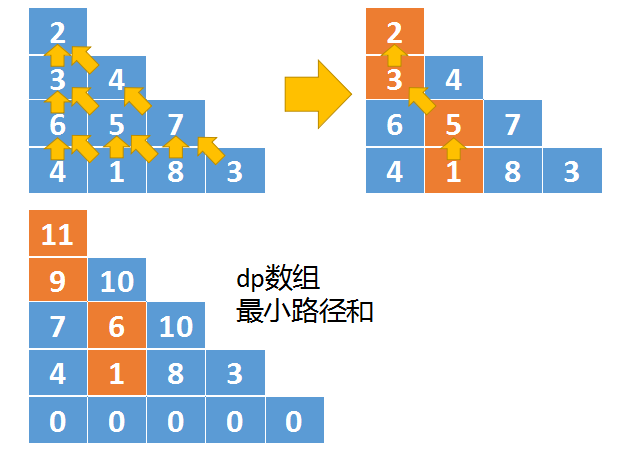
自下而上推导时，结果保存在第一行第一列中，因为三角形第一行只有一个元素，所以最终结果就保存在dp[0][0]中
此外dp数组跟自上而下比也有些变化，这里的dp数组是原始数组的行数+1
之所以以要多加一行，是因为状态转移公式变化导致的，为了处理一些边界条件所以增加了一行
以自下而上的角度看，三角形中任意一个位置triangle[i][j]，只有两个值能移动到这个这里分别是triangle[i+1][j+1]，以及triangle[i+1][j]，如下图所示
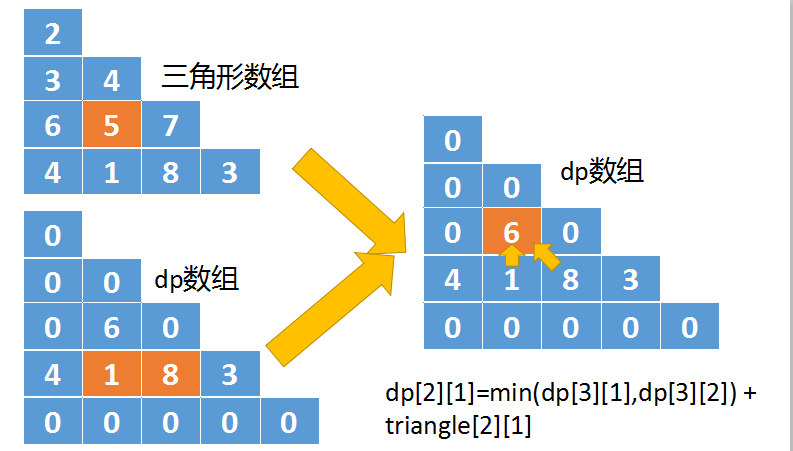
对于triangle[2][1]这个位置，它是从triangle[3][2]，以及triangle[3][1]这两个位置移动而来的。而这两个值保存在dp[3][2]和dp[3][1]中。
我们从dp[3][2]和dp[3][1]中选择一个较小的值，这里是1，然后再加上triangle[2][1]的值5，将结果6保存到dp[2][1]中。
其dp转移公式为：

复制代码

1
2
dp[i][j] = min(dp[i+1][j+1],dp[i+1][j]) + triangle[i][j]

自下而上推导没有自上而下那么直观，但是省去了一些细节处理过程
同时最终的结果就保存在了dp[0][0]中，又省去了一次遍历求min的过程
时间复杂度:O(N^2)
空间复杂度:O(N^2)

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
	int minimumTotal(vector<vector<int>>& triangle) 
	{
		if (triangle.empty()) return 0;
		int r = triangle.size();
		int c = triangle[r-1].size();//最后一行的长度
		vector<vector<int>> dp(r + 1, vector<int>(c + 1,0));
		//自下而上推导
		for (int i = r - 1; i >= 0; i--)
		{
			int j = triangle[i].size()-1;
			while (j >= 0)
			{
				//对于三角形的每一行，从右向左计算
				dp[i][j] = min(dp[i + 1][j + 1], dp[i + 1][j]) + triangle[i][j];
				--j;
			}
		}
		//最终结果就保存在第一行第一列中
		return dp[0][0];
	}
};

在这里插入图片描述

动态规划空间优化

我们用二维数组计算dp[i][j]时只用到了dp[i+1][j+1]和dp[i+1][j]
也就是说这是一个滚动更新的过程，我们只用到了上下两行数据
求dp[i][j]时只需要dp[i+1]这一行的数据即可，dp[i+2]，dp[i+3]…这些都不需要了。
于是我们可以创建一个一维数组，其长度为三角形列数+1
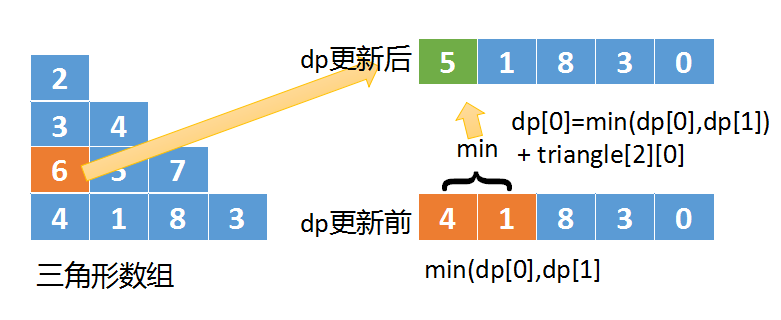
如上图所示，我们还是按照自下而上的方式，但这次的dp数组改成一维的了
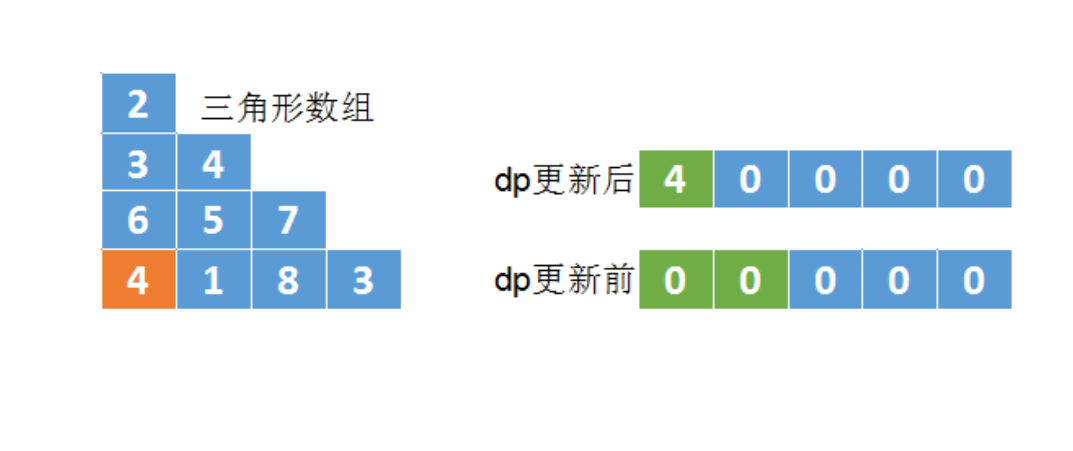
计算triangle[2][0]的最小路径为:
triangle[2][0] + min(dp[0],dp[1])
之后将结果5保存到dp[0]中
所以一维数组的状态转移方程为:
dp[j] = min(dp[j],dp[j+1]) +triangle[i][j]
我们用的是自下而上的计算方式，先计算n-1行，再计算n-2行，一直到第1行
每行计算的时候用的是从左到右的方式，如果是从右到左计算会出现值覆盖
图解演示:

在这里插入图片描述
完整代码:

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
	int minimumTotal(vector<vector<int>>& triangle) 
	{
		if (triangle.empty()) return 0;
		int r = triangle.size();
		int c = triangle[r-1].size();//最后一行的长度
		vector<int> dp(c + 1,0);
	    //自下而上推导
		for (int i = r - 1; i >= 0; i--)
		{
			//从左到右的方式计算
			for (int j = 0; j < triangle[i].size(); ++j)
			{
				dp[j] = min(dp[j], dp[j + 1]) + triangle[i][j];
			}
		}
		//dp数组的第一个元素即为最终结果
		return dp[0];
	}
};