咸鱼了半个多月了,要干点正经事了。
最近在帮老师用神经网络做多变量非线性的回归问题,没有什么心得,但是也要写个博文当个日记。
该回归问题是四个输入,一个输出。自己并不清楚这几个变量有什么关系,因为是跟遥感相关的,就瞎做呗。
- 数据预处理的选择
刚开始选取了最大最小值的预处理方法,调了很久的模型但是最后模型的输出基本不变。
换了z-score的预处理方法,模型的输出才趋于正常。
- 损失函数的选择
对于回归问题,常用的损失函数有三种,一个是平方误差函数,一个是绝对值误差函数,还有一个是交叉熵函数。
在其他参数都不变的时候分别采用这三个损失函数:
1.交叉熵
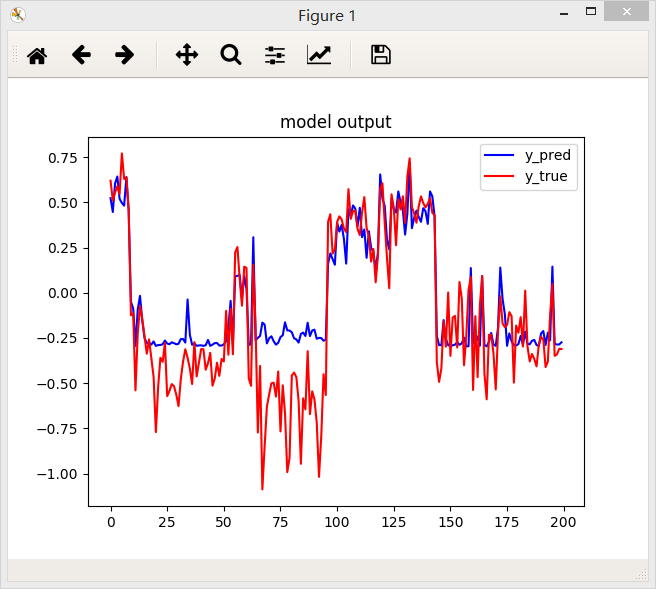
2.绝对值误差函数
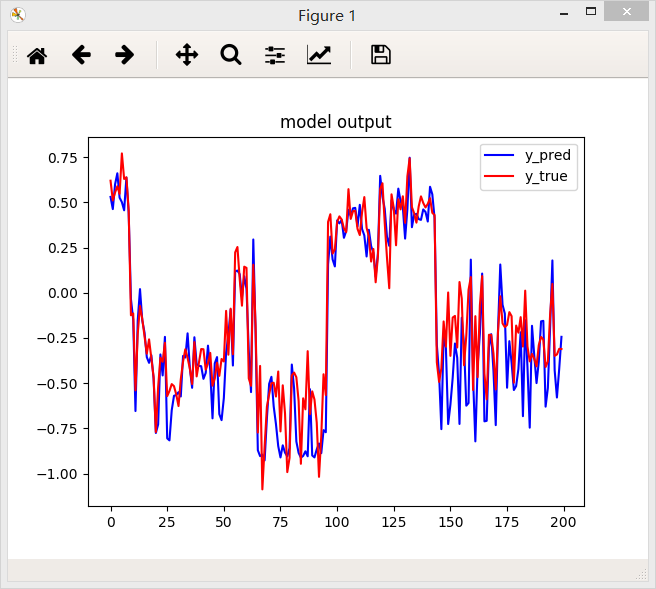
3.平方误差函数

结论:从上面三个图中国可以看出,相同条件下,绝对值误差函数得到的效果好一些。
- batch_size大小的选择
bach_size = 32
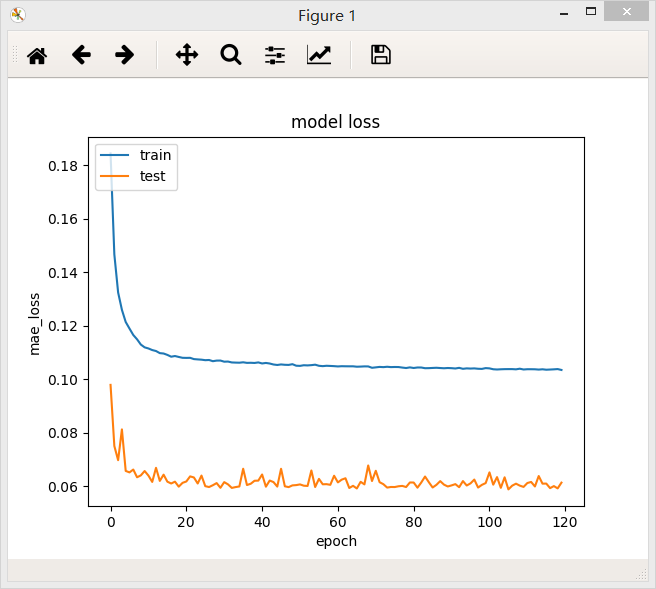
bach_size = 64
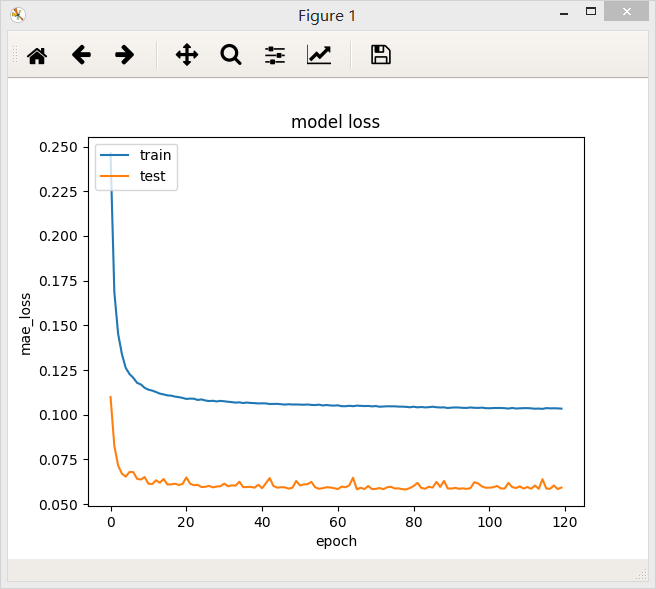
bach_size = 128
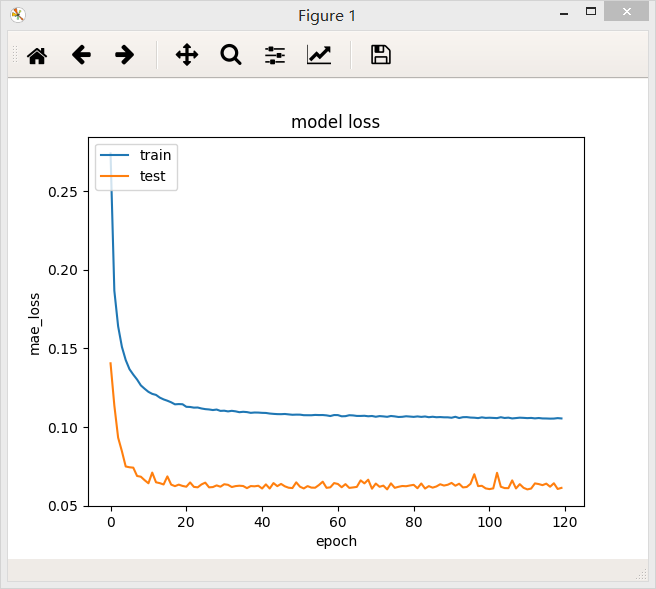
batch_size = 256
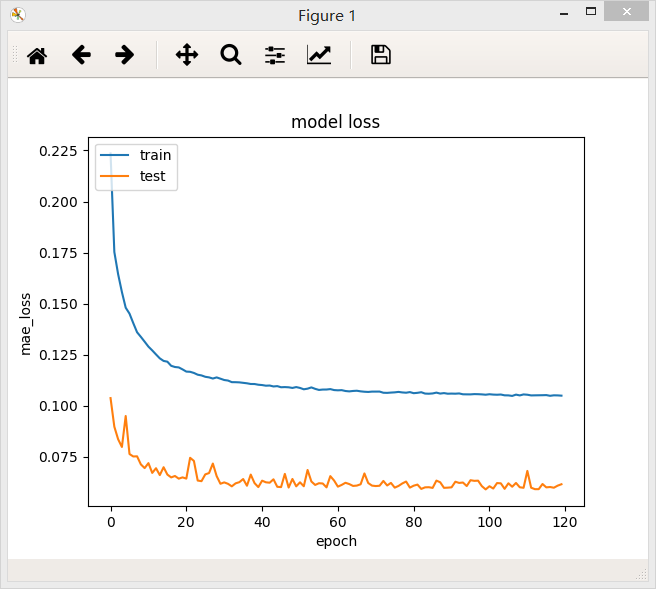
在两个不同的batch_size下,网络最后的loss值都差不多,但是在验证集上,当batch_size = 64/128时,loss曲线比较稳定。
结论:一定范围内,batch_size越大,其确定的下降方向就越准,引起训练震荡越小.随着batch_size增大,处理相同的数据量的速度越快。但是随着batchsize增大,达到相同精度所需要的epoch数量越来越多。过大的batch_size的结果是网络很容易收敛到一些不好的局部最优点。同样太小的batch_size会使得训练速度很慢,训练不容易收敛。
- 是否添Dropout层
不加dropout层
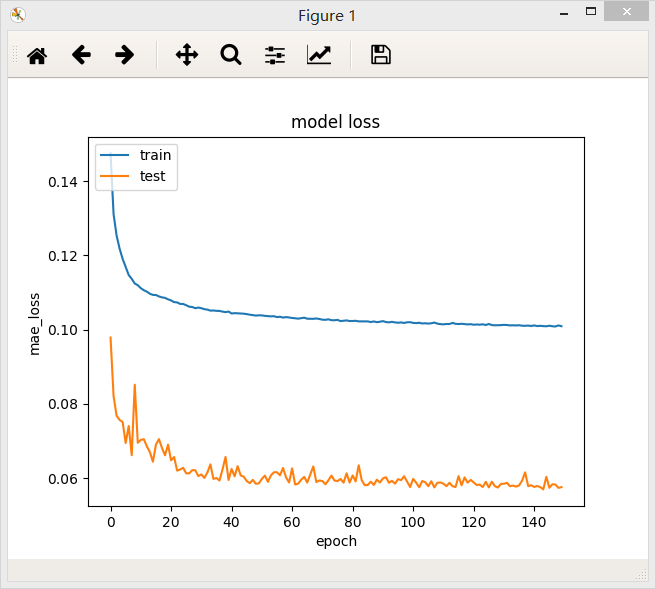
加了Dropout层

加了Dropout层后模型的loss值反而升高,但是测试集上的loss下降能平稳一些。
- 深层网络和浅层网络的选择
我自己觉得这样一个简单的问题其实浅层网络就能解决,但是老师想搭一下深度学习的车,没办法只能用比较一下两个模型。
含有一个隐层的全连接网络,64个神经元,最后模型的loss值为:0.1032
含有两个隐层的全连接网络,第一层32个神经元,第二层16个神经元,最后的loss值为0.0995
含有三个隐层的全连接网络,第一层32个神经元,第二层16个神经元,第三层8个神经元,最后模型的loss值为0.0986
含有四个隐层的全连接网络,第一层32个神经元,第二层16个神经元,第三层8个神经元,第四层4个神经元,最后模型的loss值为0.0993
含有五个隐层的全连接网络,第一层32个神经元,第二层16个神经元,第三层8个神经元,第四层4个神经元,第五层2个神经元,最后模型的loss值为0.0991
含有五个隐层的全连接网络,第一层32个神经元,第二层16个神经元,第三层8个神经元,第四层4个神经元,第五层2个神经元,第六层2个神经元,最后模型的loss值为0.0988
........
结论:在一定范围内,随着网络层的加深,模型的准确率升高。超过一定范围,随着网络层的加深,模型的准确率不但不升反而下降,测试集上的准确率也会下降,所以这并不是出现了过拟合。
- 模型宽度的选择
由于上一个实验中三层模型的loss值最低,所以我选择三层模型来做这个对于模型宽度选择的实验。
1、含有三个隐层的全连接网络,第一层32个神经元,第二层16个神经元,第三层8个神经元,最后模型的loss值为0.0986
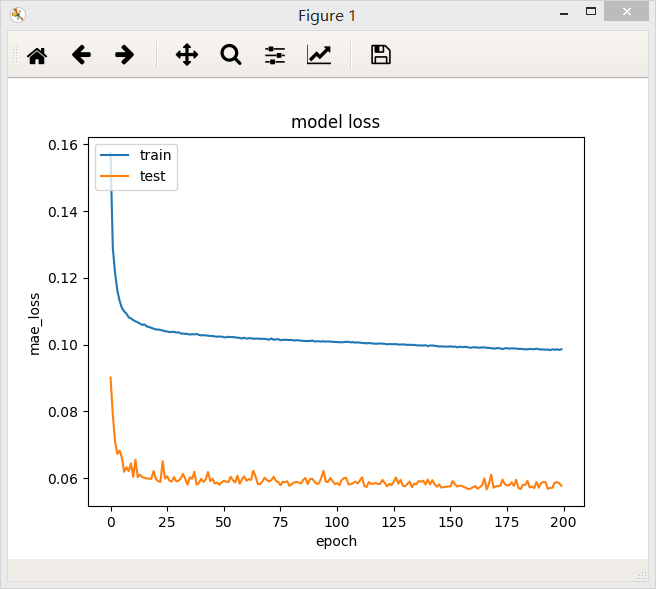
2、含有三个隐层的全连接网络,第一层32个神经元,第二层32个神经元,第三层16个神经元,最后模型的loss值为0.0986
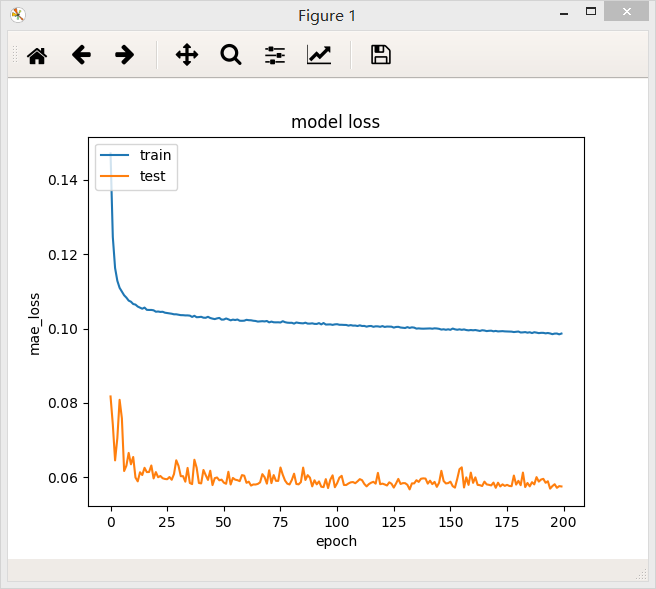
3、含有三个隐层的全连接网络,第一层32个神经元,第二层32个神经元,第三层32个神经元,最后模型的loss值为0.0960
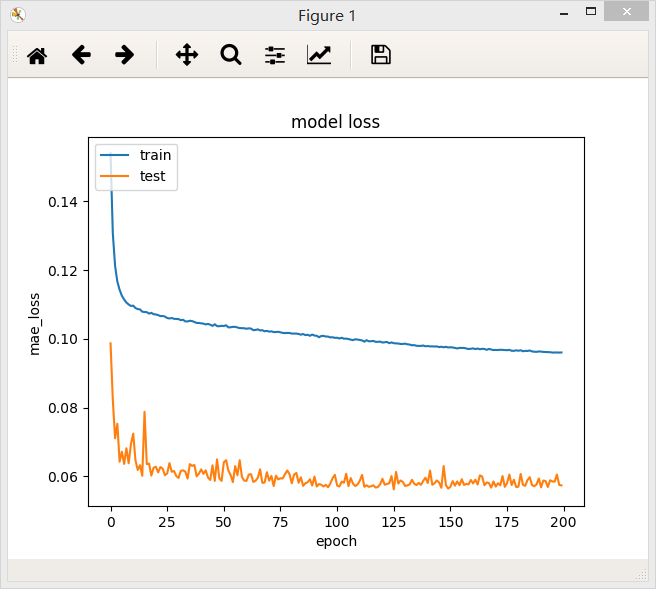
4、含有三个隐层的全连接网络,第一层32个神经元,第二层64个神经元,第三层32个神经元,最后模型的loss值为0.0967
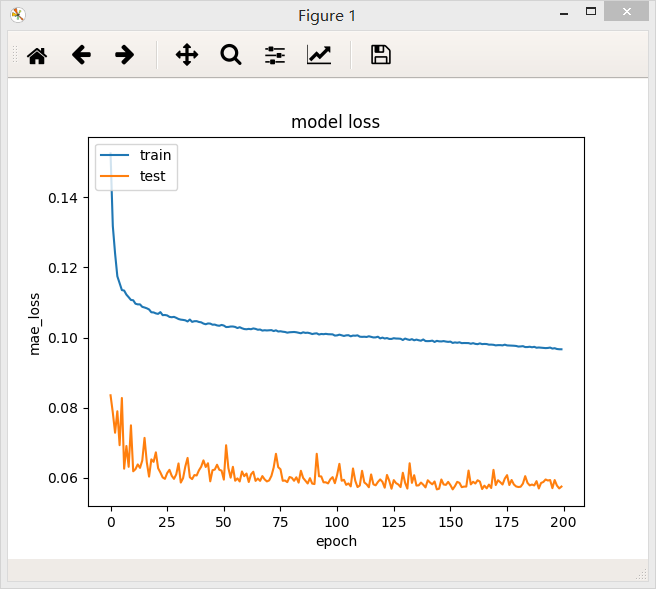
5、含有三个隐层的全连接网络,第一层32个神经元,第二层64个神经元,第三层64个神经元,最后模型的loss值为0.0967

结论:在一定范围内,网络模型越宽,模型的准确率越高,但是超过某一阈值后,模型的准确率不再提高,测试集上loss下降震荡越来越明显,说明模型的复杂度已经高于回归问题真是模型的复杂度。
- 尝试残差网络
第一种残差网络:
def identity_block(x):
out = Dense(32)(x)
#out = BatchNormalization()(out)
out = Activation('tanh')(out)
#out = Dropout(0.1)(out)
out = Dense(32)(x)
#out = Dropout(0.1)(out)
#out = BatchNormalization()(out)
out = Activation('tanh')(out)
out = Dense(4)(out)
#out = BatchNormalization()(out)
out = merge([out,x],mode='sum')
out = Activation('tanh')(out)
return out

结论:和全连接网络相比,残差网络loss下降很快,测试集上loss下降曲线很平滑,但是模型的准确率却不如普通三层的全连接网络,最终的loss值为0.1021。
第二种残差网络:
def fc_block(x):
out = Dense(32)(x)
out = Activation('tanh')(out)
out = Dense(32)(x)
out = Dropout(0.1)(out)
out = Activation('tanh')(out)
out = Dense(32)(out)
x = Dense(32)(x)
out = merge([out, x], mode = 'sum')
out = Activation('tanh')(out)
return out
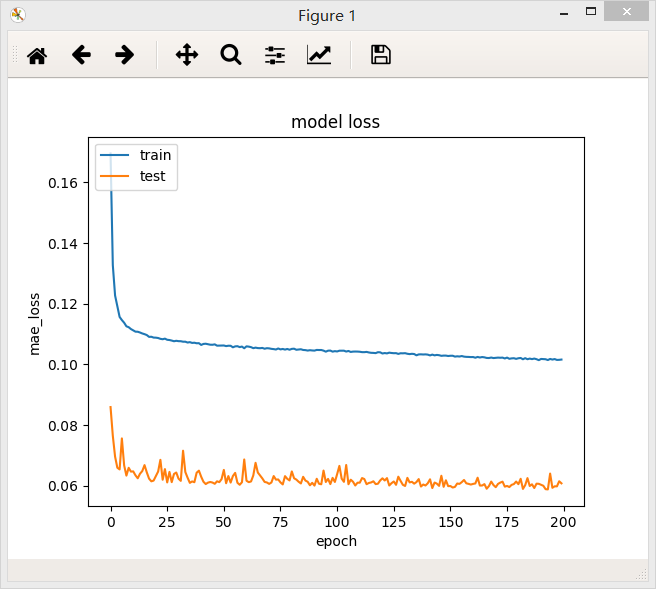
结论:第二种残差网络的loss值为0.1016,比第一种残差网络的效果能好一点。在ResNet中,这两个模块是交替使用的。
将两个模块叠加之后,模型的准确率并没有提升,应该是模型过度复杂了,最后模型的loss值为0.1027。
- relu还是tanh
由于输出值的范围是[-1, 1],因此模型的输出层的激活函数只能选择tanh。
在隐藏层中,可以选择relu和tanh作为隐藏层的激活函数。
模型结构为3层,神经元分别是32,32,32。就是上一个步骤中loss最低的网络结构,在上一个步骤中隐层的激活层使用的是tanh,loss值为0.0960
将tanh换成relu:

采用relu作为激活函数,模型的计算速度会加快,因为求导很简单。在这个问题只使用relu会使模型的准确率下降。一般在复杂的模型中使用relu比较多。
转载于:https://www.cnblogs.com/catpainter/p/8891091.html
最后
以上就是听话钥匙最近收集整理的关于keras神经网络做简单的回归问题的全部内容,更多相关keras神经网络做简单内容请搜索靠谱客的其他文章。








发表评论 取消回复