1. 首页
  2. 文章中心
  3. 经验分享

树状结构(多叉树)在数据库中的设计与存储

65 阅读 0 评论
我是靠谱客的博主 殷勤树叶，最近开发中收集的这篇文章主要介绍树状结构(多叉树)在数据库中的设计与存储，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

无限分层的树状结构，应该如何设计数据库的表结构，并进行存储呢？前段时间被这个老生常谈的问题折磨的遍体鳞伤，正好利用本文给大家做一次分享与记录。当然，这只是一位技术小学生个人见解，肯定还有更优解，欢迎指导！

读完本文，不仅可以获得树状结构存储的数据表结构，还可以获取如何存储的具体实现代码，更有新增节点等操作类的实现思路。满满的代码干货！
本文源码资源： 示例代码资源

首先，先给一个树形结构数据的示例，本文就对它进行蹂躏了：
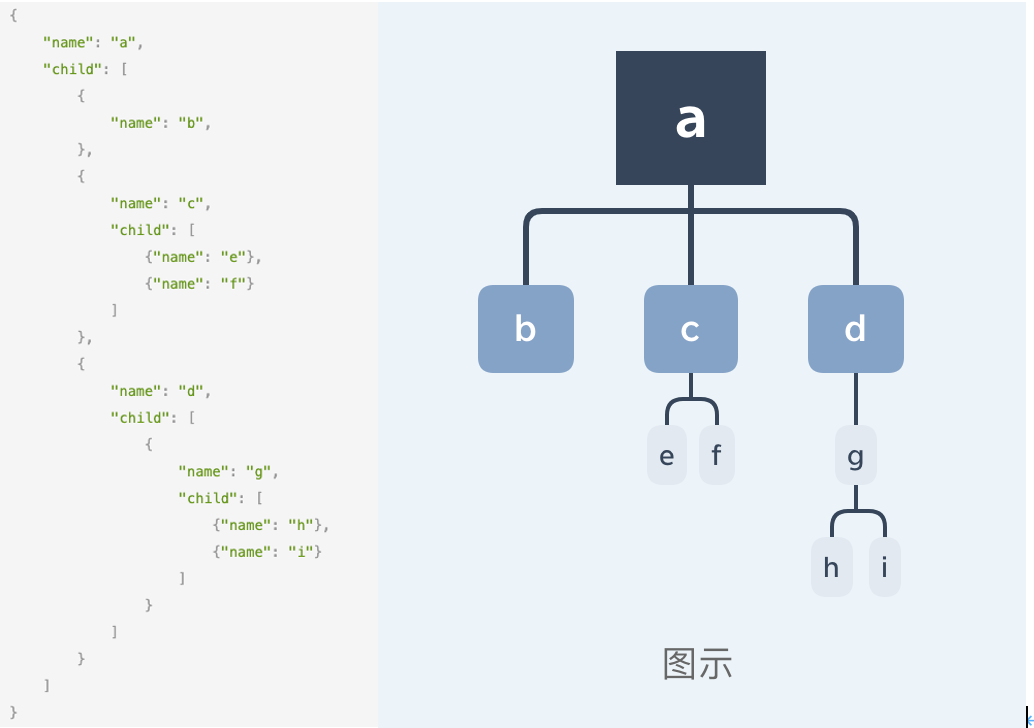
树形结构数据示例

一、数据表的设计

本次存储，要考虑节点之间的继承关系，利用pid与level来实现。同时，为避免树形结构查询时的“递归”过程，还需增加节点左右索引值。

优点：查询当前节点的父级节点或全部子节点或指定层级的节点很容易实现；
缺点：当插入或删除某节点时，大于当前节点的右索引值的全部节点都需全部更新。

比较适用于查询较多，插入与更新较少的场景
若是插入与更新较多的场景，那就不必维护lft与rgt

数据库设计表结构如下：

CREATE TABLE `node`
(
    `id`    int(11)     NOT NULL AUTO_INCREMENT COMMENT '节点ID',
    `pid`   int(11)     NOT NULL DEFAULT '0' COMMENT '父节点ID',
    `lev`   int(11)     NOT NULL DEFAULT '0' COMMENT '当前节点层级，0-N',
    `lft`   int(11)     NOT NULL DEFAULT '0' COMMENT '当前节点左索引值',
    `rgt`   int(11)     NOT NULL DEFAULT '0' COMMENT '当前节点右索引值',
    `title` varchar(32) NOT NULL DEFAULT '' COMMENT '节点标题',
    PRIMARY KEY (`id`),
    KEY `lft` (`lft`),
    KEY `rgt` (`rgt`)
) ENGINE = InnoDB DEFAULT CHARSET = utf8mb4 COMMENT ='节点信息表';

二、数据的存储实现

1. 整体思路
  • 递归获取全路径path，并获取前序遍历后的数据treeMap
  • 利用path与treeMap为树创建索引「父节点pid、当前节点层级level」
  • 递归插入树数据，并更新当前节点左右索引值lft与rgt
2. 递归获取path、treeMap

代码思路：
获取路径path是为第二步创建索引所准备；
获取数据treeMap是为方便存入数据库的数据形式；
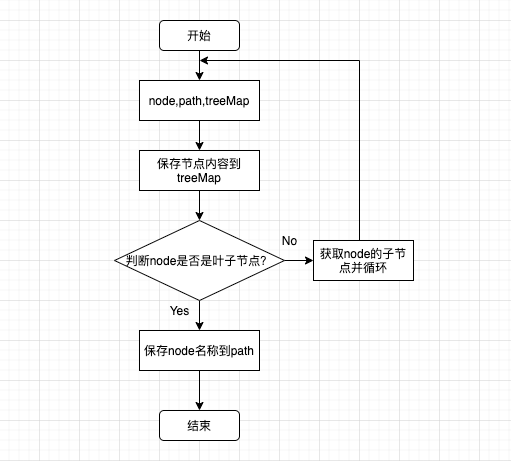
递归获取path、treeMap
具体代码：

# 递归处理 获取全路径path、树节点信息treeMap
def processTreeNode(node, path, tmpPath, treeMap):
    tmpData = copy.deepcopy(node)
    tmpData['pid'], tmpData['left'], tmpData['right'], tmpData['level'] = '', 0, 0, 0
    treeMap[tmpData['name']] = tmpData

    if 'child' not in node.keys() or len(node['child']) <= 0:
        path.append(tmpPath)
        return
    else:
        del tmpData['child']

    for childNode in node['child']:
        cTmpPath = copy.deepcopy(tmpPath)
        cTmpPath.append(childNode['name'])
        processTreeNode(childNode, path, cTmpPath, treeMap)

获取到的path、treeMap:

# path json格式
[["a", "b"], ["a", "c", "e"], ["a", "c", "f"], ["a", "d", "g", "h"], ["a", "d", "g", "i"]]

#treeMap json格式
{
      "a": {"name": "a","pid": "","left": 0,"right":0,"level": 0},
      "b": {"name": "b","pid": "","left": 0,"right": 0,"level": 0},
      "c": {"name": "c","pid": "","left": 0,"right": 0,"level": 0},
      "d": {"name": "d","pid": "","left": 0,"right": 0,"level": 0},
      "e": {"name": "e","pid": "","left": 0,"right": 0,"level": 0},
      "f": {"name": "f","pid": "","left": 0,"right": 0,"level": 0},
      "g": {"name": "g","pid": "","left": 0,"right": 0,"level": 0},
      "h": {"name": "h","pid": "","left": 0,"right": 0,"level": 0},
      "i": {"name": "i","pid": "","left": 0,"right": 0,"level": 0}
}
3. 创建索引pid、level

代码思路：
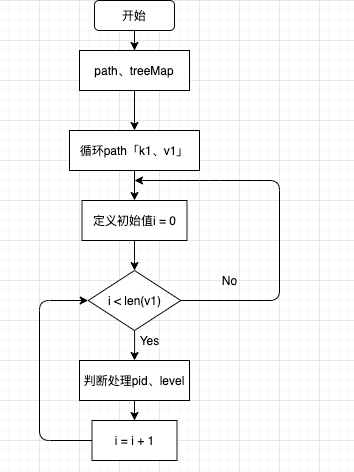
创建索引pid、level
具体代码：

# 创建树索引
def createTreeIndex(path, data):
    for k1, v1 in enumerate(path):
        i = 0
        while i < len(v1):
            id, pid = v1[i], 0

            if 0 < i < len(v1):
                pid = v1[i - 1]

            # 不存在节点,直接跳过
            if id not in data:
                continue
            #  处理pid
            if data[id]['pid'] == '':
                data[id]['pid'] = pid
            # 处理level
            if data[id]['level'] == 0:
                data[id]['level'] = i

            i = i + 1
    return

获取到的treeMap：

{
	"a": {"name": "a", "pid": 0, "left": 0, "right": 0, "level": 0}, 
	"b": {"name": "b", "pid": "a", "left": 0, "right": 0, "level": 1}, 
	"c": {"name": "c", "pid": "a", "left": 0, "right": 0, "level": 1}, 
	"e": {"name": "e", "pid": "c", "left": 0, "right": 0, "level": 2}, 
	"f": {"name": "f", "pid": "c", "left": 0, "right": 0, "level": 2}, 
	"d": {"name": "d", "pid": "a", "left": 0, "right": 0, "level": 1}, 
	"g": {"name": "g", "pid": "d", "left": 0, "right": 0, "level": 2}, 
	"h": {"name": "h", "pid": "g", "left": 0, "right": 0, "level": 3}, 
	"i": {"name": "i", "pid": "g", "left": 0, "right": 0, "level": 3}
}
4. 插入数据，并更新lft与rgt

目前为止，除过节点的左右索引值外，节点的父节点、层级均已获得，我们将采取递归的方式来存储节点更新索引。

代码思路：
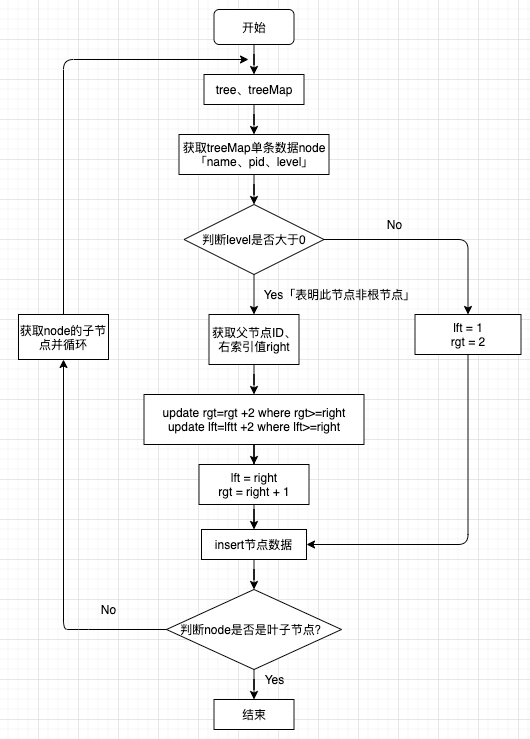
插入数据，并更新lft与rgt
简单来说，在插入节点数据时，每次都需要更新其余部分节点的左右索引值，从代码实现来看相对简单，但效率却是比统一更新索引值慢「我的需求对这个初始数据插入效率没有要求，故采用这种方式，但还是要在后续中找到最优解」

具体代码：

# 插入数据
def insertTree(tree, treeMap):
    node = treeMap[tree['name']]
    name, pid, level = node['name'], node['pid'], node['level']
    if level > 0:
        parentObj = MU.fetchone('tree', 'SELECT `id`,`rgt` FROM node WHERE `title`= "%s";' % pid)
        pid, left, right = parentObj[0], parentObj[1], parentObj[1] + 1

        MU.execute('tree', 'UPDATE node SET rgt = rgt + 2 WHERE rgt >= %d;' % left)
        MU.execute('tree', 'UPDATE node SET lft = lft + 2 WHERE lft >= %d;' % left)
    else:
        left, right = 1, 2

    insertSql = 'INSERT INTO node ( pid, lev, lft,rgt, title ) VALUES ( %d, %d, %d, %d, "%s" )' % (
        pid, level, left, right, name)
    MU.execute('tree', insertSql)

    if 'child' in tree.keys() and len(tree['child']) > 0:
        for child in tree['child']:
            insertTree(child, treeMap)

    return

更新节点的左右索引值比较麻烦，逻辑上也不好理解，下面我直接用图示举例说明：
以此类推，插入节点的同时不断地更新左右索引值。
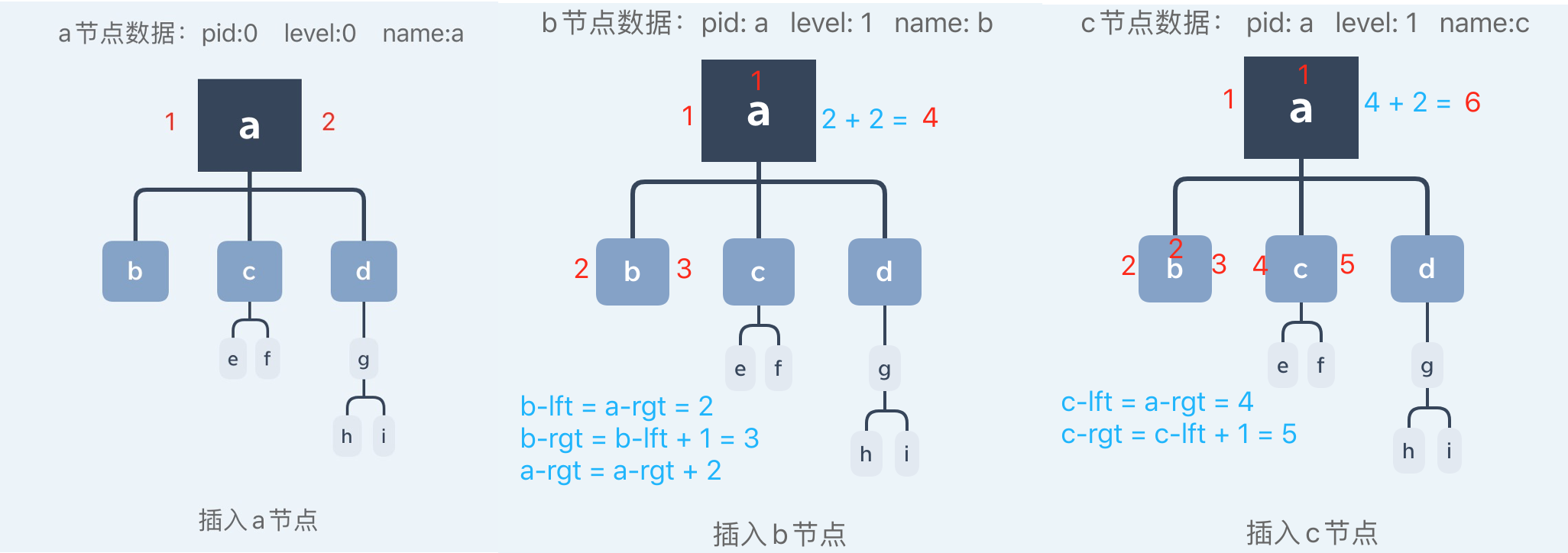
在这里插入图片描述
到此为止，树状结构数据的存储已经完成。

三、节点操作实现思路

1. 判断lft与rgt是否有重复
SELECT * FROM node s WHERE( s.lft, s.rgt ) IN (SELECT lft,rgt FROM node GROUP BY lft,rgt HAVING count(*) > 1);
2. 获取N1节点的所有子孙节点
SELECT @Lft = lft, @Rgt = rgt FROM node WHERE id = N1.id
SELECT * FROM node WHERE lft > @Lft AND rgt < @Rgt

# N1节点的所有子孙节点个数
(@Rgt - @Lft - 1) / 2
3. 获取N1节点的第一层子节点
SELECT @Lft = lft, @Rgt = rgt, @Lev = lev FROM node WHERE id = N1.id
SELECT * FROM node WHERE lft > @Lft AND rgt < @Rgt AND lev = @Lev + 1

# 获取N1节点的任意一层子节点，只需将where条件中的lev改变即可
4. 向N1节点插入子节点N2
SET XACT_ABORT ON  
BEGIN TRANSCTION  
SELECT @Rgt = rgt, @Lev = lev FROM node WHERE id = N1.id
UPDATE node SET rgt = rgt + 2 WHERE rgt >= @Rgt
UPDATE node SET lft = lft + 2 WHERE lft >= @Rgt
INSERT INTO node(title, pid, lev, lft, rgt) values(N2.title, N1.id, @Lev + 1, @Rgt, @Rgt + 1)
COMMIT TRANSACTION  
SET XACT_ABORT OFF
5. 向N1节点插入兄弟节点N2
SET XACT_ABORT ON  
BEGIN TRANSCTION  
SELECT @Rgt = rgt, @Pid = pid, @Lev = lev FROM node WHERE id = N1.id
UPDATE node SET rgt = rgt + 2 WHERE rgt >= @Rgt
UPDATE node SET lft = lft + 2 WHERE lft >= @Rgt
INSERT INTO node(title, pid, lev, lft, rgt) values(N2.title, @Pid, @Lev, @Rgt + 1, @Rgt + 2)
COMMIT TRANSACTION  
SET XACT_ABORT OFF
4. 删除N1节点及其全部子节点
SET XACT_ABORT ON  
BEGIN TRANSCTION  
SELECT @Lft = lft, @Rgt = rgt FROM node WHERE id = N1.id
DELETE FROM node WHERE lft >= @Lft AND rgt <= @Rgt  
UPDATE node SET lft = lft – (@Rgt - @Lft + 1) WHERE lft > @Lft  
UPDATE node SET rgt = rgt – (@Rgt - @Lft + 1) WHERE rgt > @Rgt  
COMMIT TRANSACTION  
SET XACT_ABORT OFF

本文源码资源： 示例代码资源

最后

以上就是殷勤树叶为你收集整理的树状结构(多叉树)在数据库中的设计与存储的全部内容，希望文章能够帮你解决树状结构(多叉树)在数据库中的设计与存储所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(43)

相关文章

微人事第十天：Spring Security基于数据库的认证
微人事第十天：Spring Security基于数据库的认证
微人事项目实战的数据库脚本_简化微人事部署，Flyway 搞起来
微人事项目实战的数据库脚本_简化微人事部署，Flyway 搞起来
微人事-服务端菜单接口设计
微人事-服务端菜单接口设计
微人事-基础信息设置-职称管理后端接口设计
微人事-基础信息设置-职称管理后端接口设计
树状结构(多叉树)在数据库中的设计与存储
树状结构(多叉树)在数据库中的设计与存储
微人事（10）- 完善权限管理1 完善权限管理
微人事（10）- 完善权限管理1 完善权限管理
微人事项目实战的数据库脚本_人事管理系统项目合集
微人事项目实战的数据库脚本_人事管理系统项目合集
微人事第二天：容器相关配置
微人事第二天：容器相关配置

评论列表共有 0 条评论

立即
投稿
返回
顶部