『SPOJ 687』repeats

86 阅读 0 评论 57 点赞

我是靠谱客的博主年轻鞋子，最近开发中收集的这篇文章主要介绍『SPOJ 687』repeats，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

转载声明:http://blog.csdn.net/kongming_acm/article/details/6321363
论文转载:
http://wenku.baidu.com/link?url=xBx1136joEtqVhvjmGnFgsJ9c5LLr9aw2AsupDH8u2UpucAZB2J9WAFc48o6ZU-xphWysH8HAJZLwvImlfg36cJAQJfP3VejDonakPI3_Ey】

题意:简单明了,就是找一个子串重复最多次而形成的.

个人感想:
刚看到这道题的时候,我也是一脸懵逼啊…我还想用自己的能力去想想该怎么做,我是毫无想法,看了论文,我是一头雾水了,还是自己的能力还没达到这样的程度啊.我是看这转载然后硬刚究竟什么回事.这道题也是出乎我的感觉…我想通过我的硬钢想法来描绘一下这代码.

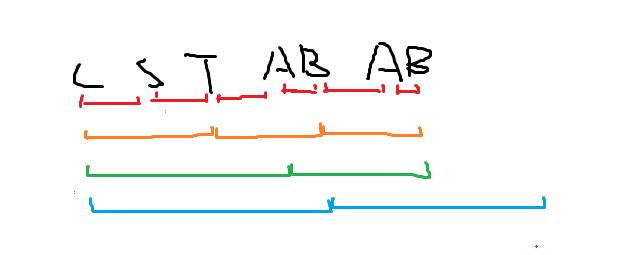
这里写图片描述
首先我们知道,循环的次数1是必然的.我们现在要找2次以上的.

代码的意思是先枚举循环节
红色代表长度为1的循环节.
橙色代表长度为2的循环节.
绿色代表长度为3的循环节.
蓝色代表长度为4的循环节.(4的循环节肯定是不存在的,超出了最长长度了)
假设长度为L.
假设当前的左点为i,右点为j

我每条横线上都有一个小点,代表枚举的时候,我要知道这两个位置上的最长公共前缀lcp.
这有什么用了? 通过这个我们就可以之后两个串能过延伸最长长度k,通过 k/L.我们就知道这两个串的 循环节个数 可是只往右边枚举不行啊. 我们得尝试的往左一步求循环节个数 因为我们知道 k%L是不一定能整除的,但是当k>L的时候,其实**（j-i）**,这块就已经是循环节了.
可以试这画画究竟是不是.

但是多出来的部分k%L！=0 多出来的又是怎么一回事呢?我们又得怎么处理呢?
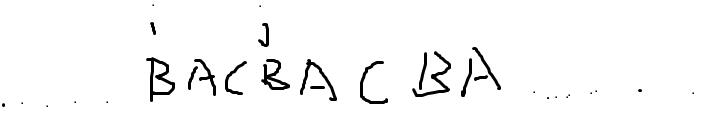
这里写图片描述
我们看看这个图,(i,j)的公共前缀=5.
但是我们的循环节长度为3!这超过了2.我先跟我一步步来
（）代表着匹配的长度

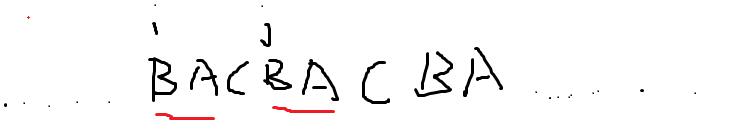这里写图片描述（1）
（2）
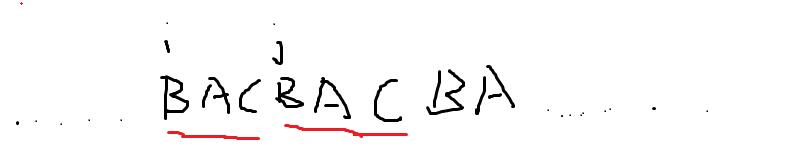（3）
这时候我们知道循环节已经**=3**,那么这时候的循环节是BAC,因为刚好k满足3.

这是我们就可以往左匹配一下,如果**（i-（l-k%l ) ,j-（l-k%l ))>=3**,那么我们的循环节必然就可以再**+1**

注意！还没完,因为(i,j)的公共前缀是5,接着继续!
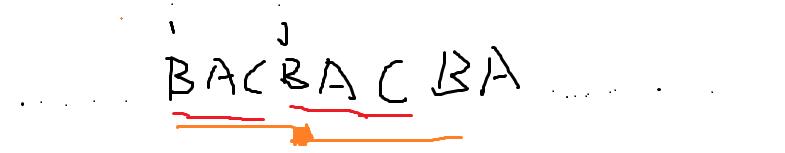这里写图片描述（4）
是不是发现我的j点的颜色加深了,没错这时候的循环节就可以发生改变了为ACB.

这我们就可以比较**（i-2，j-2）的公共前缀是不是>=2**，我们就可以多**+1循环节啦！
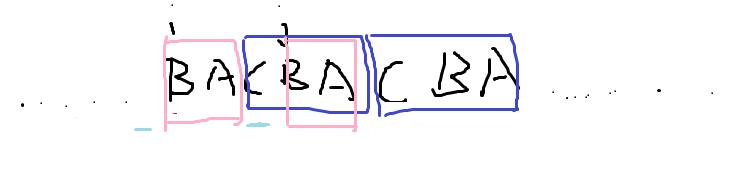（5）
同样道理就是,这时就可以直接比较（i-1，j-1）是不是>=1,我们又可以+1循环节**

这就是为什么结果往左的时候要用到**（i-（l-k%l ) ,j-（l-k%l ))，这是一个微妙的贪心策略**.

这时看到代码的时候,我们会发现一个问题,就是为什么枚举长度的时候, 只需要枚举**（i,L）(L,2L),
(2L，3*L）…这样的情况,例如L=2**,它绝对不需要枚举到**(1,3),
因为这样枚举的时候,如果循环节满足长度为2**,那么不管L=2,的区间怎么枚举,他都会触碰到
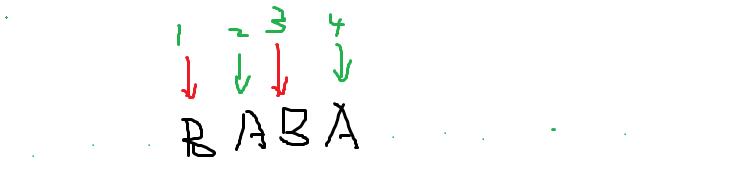
这里写图片描述
不伦检测**（1，3）,还是（2，4）那么他整个循环节我都可以检测出来,往,通过往左修正一样能是得到同样结果…这是我感觉出来的**,可能这是循环节的特性吧…我也不太懂.

代码:

/* Author:GavinjouElephant
 * Title:
 * Number:
 * main meanning：
 *
 *
 *
 */

//#define OUT
#include <iostream>
using namespace std;
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <sstream>
#include <cctype>
#include <vector>
#include <set>
#include <cstdlib>
#include <map>
#include <queue>
//#include<initializer_list>
//#include <windows.h>
//#include <fstream>
//#include <conio.h>
#define MaxN 0x7fffffff
#define MinN -0x7fffffff
#define Clear(x) memset(x,0,sizeof(x))
const int INF=0x3f3f3f3f;

int T;
const int maxn=500000;
int t1[maxn];
int t2[maxn];
int c[maxn];
int N;
char in[2];
char s[maxn];
int t[maxn];
bool cmp(int * r,int a,int b,int l)
{
    return r[a]==r[b] &&r[a+l]==r[b+l];
}
void da(char str[],int sa[],int Rank[],int height[],int n,int m)
{
    n++;
    int i,j,p;
    int* x=t1;
    int* y=t2;
    for(i=0;i<m;i++) c[i]=0;
    for(i=0;i<n;i++) c[x[i]=str[i]]++;
    for(i=1;i<m;i++) c[i]+=c[i-1];
    for(i=n-1;i>=0;i--)sa[--c[x[i]]]=i;

    for(j=1;j<=n;j<<=1)
    {
        p=0;
        for(i=n-j;i<n;i++)y[p++]=i;
        for(i=0;i<n;i++)if(sa[i]>=j)y[p++]=sa[i]-j;

        for(i=0;i<m;i++)c[i]=0;
        for(i=0;i<n;i++)c[x[y[i]]]++;
        for(i=1;i<m;i++) c[i]+=c[i-1];
        for(i=n-1;i>=0;i--)sa[--c[x[y[i]]]]=y[i];

        swap(x,y);
        p=1;
        x[sa[0]]=0;
        for(i=1;i<n;i++)
        x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
        if(p>=n)break;
        m=p;
    }
    int k=0;
    n--;
    for(i=0;i<=n;i++)Rank[sa[i]]=i;
    for(i=0;i<n;i++)
    {
        if(k)k--;
        j=sa[Rank[i]-1];
        while(str[i+k]==str[j+k])k++;
        height[Rank[i]]=k;

    }

}
int sa[maxn];
int rk[maxn];
int height[maxn];
int dpmin[maxn][25];
void cdpmin(int n)
{
    int i,j;
    for(i=1;i<=n;i++) dpmin[i][0]=height[i];
    for(j=1;j<=log(double(n+1))/log(2.0);j++)
    {

        for(i=1;i+(1<<j)-1<=n;i++)
        {
            dpmin[i][j]=min(dpmin[i][j-1],dpmin[i+(1<<(j-1))][j-1]);

        }
    }

}
int get_min(int x,int y)
{

    int k=(int)(log(double(y-x+1))/log(2.0));

    return min(dpmin[x][k],dpmin[y-(1<<k)+1][k]);

}

int get_min_lcp(int x,int y)

{

    x=rk[x],y=rk[y];

    if(x>y) swap(x,y);

    x++;

    int k=(int)(log(double(y-x+1))/log(2.0));

    return min(dpmin[x][k],dpmin[y-(1<<k)+1][k]);

}
int main()
{
#ifdef OUT
    freopen("coco.txt","r",stdin);
    freopen("lala.txt","w",stdout);
#endif
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&N);
        for(int i=0;i<N;i++)
        {
            scanf("%s",in);
            s[i]=in[0];
        }
        s[N]='';
        da(s,sa,rk,height,N,256);

        cdpmin(N);
        int ans=0;
        for(int i=1;i<N;i++)//长度为i的子串
        {
            for(int j=0;j+i<N;j+=i)
            {
                int k=get_min_lcp(j,j+i);
                int now=k/i;
                int tj=j-(i-k%i);
                if(tj>=0)
                    if(get_min_lcp(tj,tj+i)>=(i-k%i)) now++;
                if(now+1>ans) ans=now+1;
            }

        }

        printf("%dn",ans);

    }

    return 0;
}