概述
题目：给定一个字符串，求重复次数最多的连续重复子串。
思路:先穷举长度L，然后求长度为L的子串最多能连续出现几次。首先连续出现1次是肯定可以的，所以这里只考虑至少2次的情况。假设在原字符串中连续出现2次，记这个子字符串为S，那么S肯定包括了字符r[0], r[L], r[L*2],r[L*3], ……中的某相邻的两个。所以只须看字符r[L*i]和r[L*(i+1)]往前和
往后各能匹配到多远，记这个总长度为K，那么这里连续出现了K/L+1次。最后看最大值是多少。如图所示。
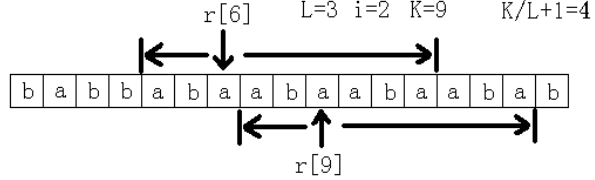
穷举长度L的时间是n，每次计算的时间是n/L。所以整个做法的时间复杂度是O(n/1+n/2+n/3+……+n/n)=O(nlogn)。
ps：基本思路在罗穗骞的论文里已经说得比较清楚了，而我在这里要提的是论文里比较模糊的部分
要提一提的总共有两点，第一点比较显而易见
“S肯定包括了字符r[0], r[L], r[L*2],r[L*3], ……中的某相邻的两个”
由于当前S是有两个长度为L的连续重复子串拼接而成的，那意味着S[i]和S[i+L](0≤i<L)必定是一样的字符
而这两个字符位置相差L
而字符r[0],r[L],r[L*2],r[L*3],......中相邻两个的位置差均为L
“只须看字符r[L*i]和r[L*(i+1)]往前和往后各能匹配到多远”，对于往后能匹配到多远，这个直接根据最长公共前缀就能很容易得到，即上图中的后缀Suffix(6)和后缀Suffix(9)的最长公共前缀。而对于往前能匹配到多远，我们当然可以一开始就把字符串反过来拼在后面，这样也能根据最长公共前缀来看往前能匹配到多远，但这样效率就比较低了。
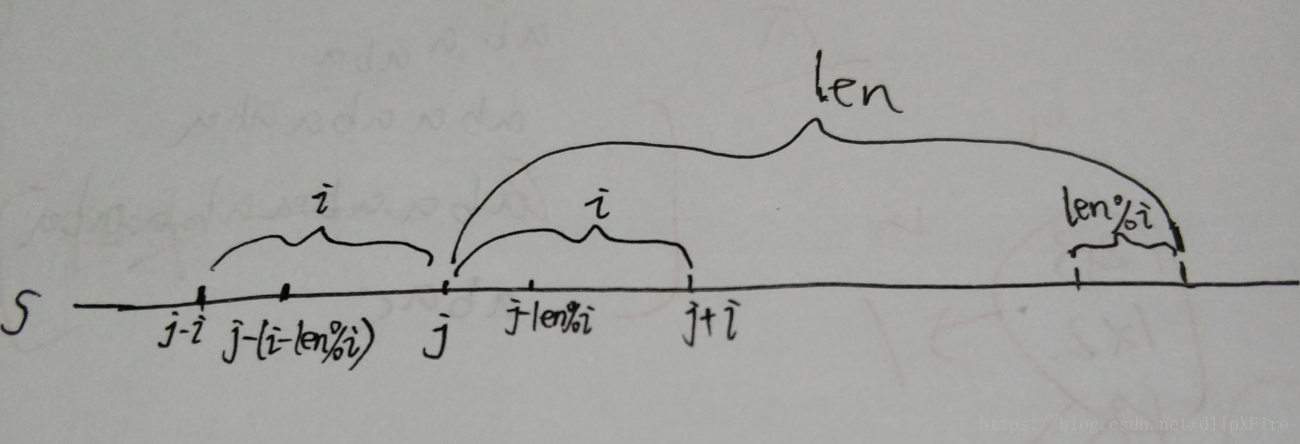
其实，当枚举的重复子串长度为i时，我们在枚举r[i*j]和r[i*(j+1)]的过程中，必然可以出现r[i*j]在第一个重复子串里，而r[i*(j+1)]在第二个重复子串里的这种情况，如果此时r[i*j]是第一个重复子串的首字符，这样直接用公共前缀k除以i并向下取整就可以得到最后结果。但如果r[i*j]如果不是首字符，这样算完之后结果就有可能偏小，因为r[i*j]前面可能还有少许字符也能看作是第一个重复子串里的。
于是，我们不妨先算一下，从r[i*j]开始，除匹配了k/i个重复子串，还剩余了几个字符，剩余的自然是k%i个字符。如果说r[i*j]的前面还有i-k%i个字符完成匹配的话，这样就相当于利用多余的字符还可以再匹配出一个重复子串，于是我们只要检查一下从r[i*j-(i-k%i)]和r[i*(j+1)-(i-k%i)]开始是否有i-k%i个字符能够完成匹配即可，也就是说去检查这两个后缀的最长公共前缀是否比i-k%i大即可。
当然如果公共前缀不比i-k%i小，自然就不比i小，因为后面的字符都是已经匹配上的，所以为了方便编写，程序里面就直接去看是否会比i小就可以了。
//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=52010;
int t1[maxn],t2[maxn],c[maxn];
bool cmp(int *r,int a,int b,int l)
{
return r[a]==r[b]&&r[a+l]==r[b+l];
}
void da(int str[],int sa[],int ra[],int height[],int n,int m)
{
n++;
int p,*x=t1,*y=t2;
for(int i=0;i<m;i++) c[i]=0;
for(int i=0;i<n;i++) c[x[i]=str[i]]++;
for(int i=1;i<m;i++) c[i]+=c[i-1];
for(int i=n-1;i>=0;i--) sa[--c[x[i]]]=i;
for(int j=1;j<=n;j<<=1)
{
p=0;
for(int i=n-j;i<n;i++) y[p++]=i;
for(int i=0;i<n;i++)
if(sa[i]>=j) y[p++]=sa[i]-j;
for(int i=0;i<m;i++) c[i]=0;
for(int i=0;i<n;i++) c[x[y[i]]]++;
for(int i=1;i<m;i++) c[i]+=c[i-1];
for(int i=n-1;i>=0;i--) sa[--c[x[y[i]]]]=y[i];
swap(x,y);
p=1;x[sa[0]]=0;
for(int i=1;i<n;i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
if(p>=n) break;
m=p;
}
int k=0;
n--;
for(int i=0;i<=n;i++) ra[sa[i]]=i;
for(int i=0;i<n;i++)
{
if(k) k--;
int j=sa[ra[i]-1];
while(str[i+k]==str[j+k])k++;
height[ra[i]]=k;
}
}
int m,n,k,t;
int ra[maxn],height[maxn],str[maxn],sa[maxn];
int mm[maxn],best[20][maxn];
void initRMQ(int n)
{
mm[0]=-1;
for(int i=1;i<=n;i++)
mm[i]=((i&(i-1))==0)?mm[i-1]+1:mm[i-1];
for(int i=1;i<=n;i++)best[0][i]=height[i];
for(int i=1;i<=mm[n];i++)
for(int j=1;j+(1<<i)-1<=n;j++)
{
int a=best[i-1][j];
int b=best[i-1][j+(1<<(i-1))];
if(a<b) best[i][j]=a;
else best[i][j]=b;
}
}
int askRMQ(int a,int b)
{
int t=mm[b-a+1];
b-=(1<<t)-1;
a=best[t][a];b=best[t][b];
return a<b?a:b;
}
int lcp(int a,int b)//求以a，b开始的子串的最长公共前缀
{
a=ra[a];b=ra[b];
if(a>b) swap(a,b);
return askRMQ(a+1,b);
}
char s[maxn];
int main()
{
/// freopen("in.txt","r",stdin);
int t;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(int i=0;i<n;i++)
{
getchar();
scanf("%c",&s[i]);
}
for(int i=0;i<n;i++)
str[i]=s[i]-'a'+1;
str[n]=0;
da(str,sa,ra,height,n,5);
/*
for(int i=1; i<=n; ++i)
{
printf("%d:t",i);
for(int j=i-1; j<n; ++j)
printf("%d",str[j]);
puts("");
}
puts("");
puts("-------------After sort---------------");
for(int i=1; i<=n; ++i)
{
printf("sa[%2d ] = %2dt",i,sa[i]);
for(int j=sa[i]; j<n; ++j)//for(int j=sa[i]; j<n; ++j)？？？
printf("%d",str[j]);
puts("");
}
puts("");
puts("---------------Height-----------------");
for(int i=1; i<=n; ++i)
printf("height[%2d ]=%2d n",i,height[i]);
puts("");
puts("----------------ra------------------");
for(int i=1; i<=n; ++i)
printf("ra[%2d ] = %2dn",i,ra[i]);
puts("------------------END-----------------");
*/
initRMQ(n);
int ans=1;
for(int i=1;i<=n;i++)
{
for(int j=0;j+i<n;j+=i)
{
int len=lcp(j,j+i);
int k=j-(i-len%i);
int sum=len/i+1;
if(k>=0&&lcp(k,k+i)>=i)
sum++;
ans=max(ans,sum);
}
}
printf("%dn",ans);
}
return 0;
}
最后
以上就是会撒娇蜜蜂为你收集整理的SPOJ - REPEATS （后缀数组，rmq,lcp 求重复次数最多的连续重复子串）的全部内容，希望文章能够帮你解决SPOJ - REPEATS （后缀数组，rmq,lcp 求重复次数最多的连续重复子串）所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复