故障诊断作业2
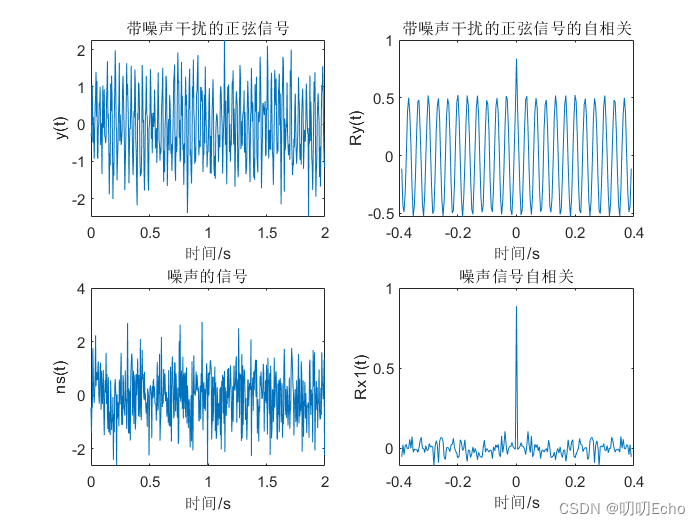
1. 请把例2.19求带噪声干扰的正弦信号和白噪声信号的自相关函数,并进行比较。
clc; %清除命令窗口的内容
clear; %清除工作空间的所有变量,函数,和MEX文件
close all; %关闭所有的figure窗口
fs=256; %采样频率
t=0:1/fs:2-1/fs; %信号的时间序列
p=length(t);
lag=100; %延迟点数
randn('state' ,0); %设置随机数的初始状态
y=sin(2*pi*30.*t)+0.6*randn(1,p); %产生原始信号
[c,lags]=xcorr(y,lag,'unbiased') ; %对信号进行无偏自相关估计
ns=randn(1,p); %产生一个长度 与信号y一样的随机号
[cns,lags]=xcorr(ns,lag,'unbiased') ; %对随机信号进行无偏自相关估计
figure(1)
subplot(221)
plot(t,y);
xlabel('时间/s' );ylabel('y(t)');
title('带噪声干扰的正弦信号');
subplot(222)
plot(lags/fs,c);
xlabel('时间/s' );ylabel('Ry(t)');
title('带噪声干扰的正弦信号的自相关');
subplot(223)
plot(t,ns);
xlabel('时间/s' );ylabel( 'ns(t)');
title('噪声的信号');
subplot(224)
plot(lags/fs,cns);
xlabel('时间/s');
ylabel('Rx1(t)');
title('噪声信号自相关'); 通过对比发现,带噪声干扰的原始正弦信号的自相关函数处理得到的峰值时间刚刚好也是噪声信号的的自相关函数的峰值时间,两者具有高度吻合。
输出打印图片如下:
2. 请给下面matlab做中文注释并运行及其比较结果做一简要对比说明。
%%XXXXXXX FFT Toterial XXXXXXXXXXXXXXXXXXXXXXXXXX
clc %清除命令窗口的内容
clear all %清除工作空间的所有变量,函数,和MEX文件
close all %关闭所有的figure窗口
%XXFFT using general form XXXXXXXXXXXXXXXXXXXXXXX
mm=[]; %给mm赋值一个空矩阵
%A=10; %给A赋值10,但好像没有用上
fs=1000; %采样频率
Ts=1/fs; %采样间隔
t=(1:1000)*Ts; %采样的分布长度向量
%产生原始信号(200Hz、400Hz、300Hz的正弦波之和)
y=10*sin(2*pi*200*t)+5*sin(2*pi*400*t)+12*sin(2*pi*300*t);
N=length(t); %信号长度
for(k=1:N) %嵌套循环 %实现一个循环,判断k是否还在1至1000里面
for(n=1:N) %实现一个循环,判断n是否还在1至1000里面
y1(n)=y(n).*exp(-j*2*pi*((-N/2)+n-1)*((-N/2)+k-1)/N);
end
mm=[mm sum(y1)]; %一个循环结束,就打印一个mm值放入数组中
end
length(mm); %读取mm的数组长度,共有上面循环收集来的1000数据
f=fs.*(-N/2:N/2-1)/N; %f为-500至499.023的点,共1024个
%figure(1)
subplot(311); %将三个图表打印图表在一起(为了方便查看)
%可能因为matlab中fft运算后需要对幅值乘2除N(变换的点数)
%所以这里也进行了幅值修正
plot(f,2*abs(mm)/N); %绘制时域信号图
%打印表头
title('Frequency spectrum for given signal without FFT biltin function');
%打印X轴标签
xlabel('Frequency(Hz)');
%打印Y轴标签
ylabel('Amplitude(volt)');
%XXXXXXXXXXXXXXXXXXXXXXXXXX FFT with biltin function
mm=[]; %给mm赋值一个空矩阵
%A=10; %给A赋值10,但好像没有用上
fs=1000; %采样频率
Ts=1/fs; %采样间隔
t=(1:1000)*Ts; %采样的分布长度向量
%产生原始信号(200Hz、400Hz、300Hz的正弦波之和)
y=10*sin(2*pi*200*t)+5*sin(2*pi*400*t)+12*sin(2*pi*300*t);
N=length(t); %信号长度
yy=fft(y); %傅里叶变换
yyy=fftshift(yy); %快速傅里叶变换零频分量移动到数组中心
f=fs.*(-N/2:N/2-1)/N; %f为-500至499.023的点,共1024个
subplot(312) %将三个图表打印图表在一起(为了方便查看)
plot(f,(2*abs(yyy)/N)); %绘制快速傅里叶变换的时域信号图
%打印表头
title('Frequency spectrum for given signal with FFT biltin function (BF)');
%打印X轴标签
xlabel('Frequency(Hz)');
%打印Y轴标签
ylabel('Amplitude(volt)');
%XXXXXXXXXXXXXXXXX FFT with biltin function and zero padding
mm=[]; %给mm赋值一个空矩阵
%A=10; %给A赋值10,但好像没有用上
fs=1000; %采样频率
Ts=1/fs; %采样间隔
t=(1:1000)*Ts; %采样的分布长度向量
%产生原始信号(200Hz、400Hz、300Hz的正弦波之和)
N= 2^nextpow2(1000); %若x的长度是2的整数次幂,函数fft运行速度最佳
yy=fft(y,N); %对数据的前n个点进行傅里叶变换
yyy=fftshift(yy); %快速傅里叶变换
f=fs.*(-N/2:N/2-1)/N; %f为-500至499.023的点,共1024个
subplot(313) %将三个图表打印图表在一起(为了方便查看)
plot(f,(2*abs(yyy)/N)); %绘制快速傅里叶变换的时域信号图
%打印表头
title('Frequency spectrum for given signal with FFT(BF)and zero padding');
%打印X轴标签
xlabel('Frequency(Hz)');
%打印Y轴标签
ylabel('Amplitude(volt)');
%XXXXXXXXXXXXXXXXXXXXXXXXXXX END 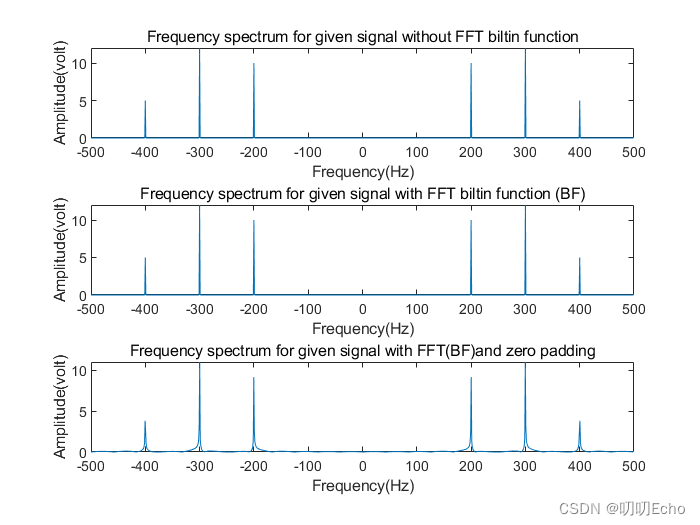
结果说明:
图一是没有经过快速傅里叶变换得到的原始信号结果图;
图二是经过快速傅里叶变换得到的信号结果图;
图三是经过零频点位移到频谱中间的快速傅里叶变换的信号结果图;
从谱图来看,三个函数都能进行较好的分辨出来峰值,其中图三在峰值带附近有小范围低频波动,其他两个函数没有。
3.请你写一写MATLAB中几种功率谱估计函数的比较分析与选择,最好举例说明。(pcov, pmcov, pyulear, pmtm, pmusic, peig, pwelch, pburg ,periodogram, arburg, prony)
一、参数设定
仿真信号:xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)
噪声信号:randn(size(n))
采样频率为:Fs=1000;
采样点数为:1024;
二、仿真结果分析比较
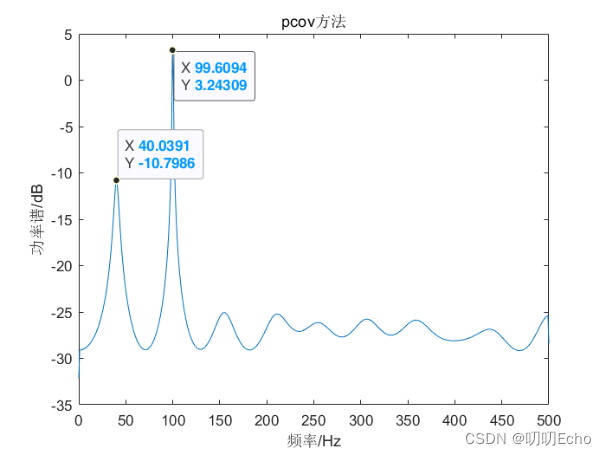
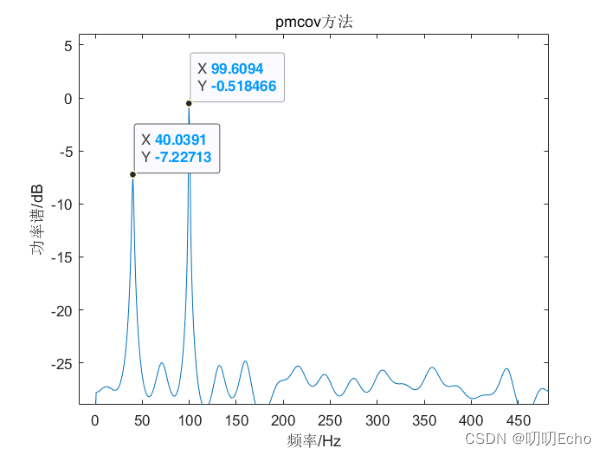
(一)将计算出的功率谱经10*log10(Px)换算成分贝单位,绘制如图1-10所示:
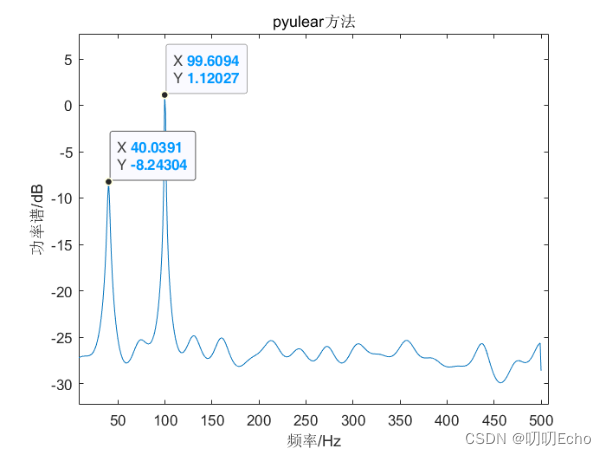
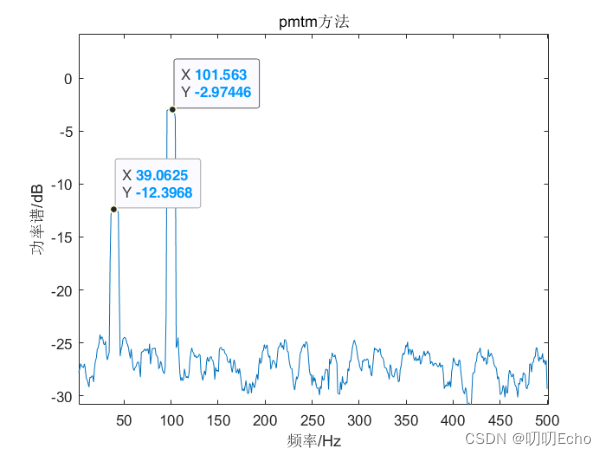
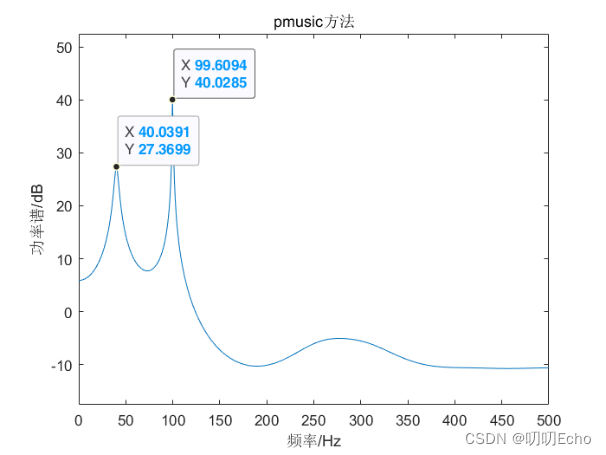
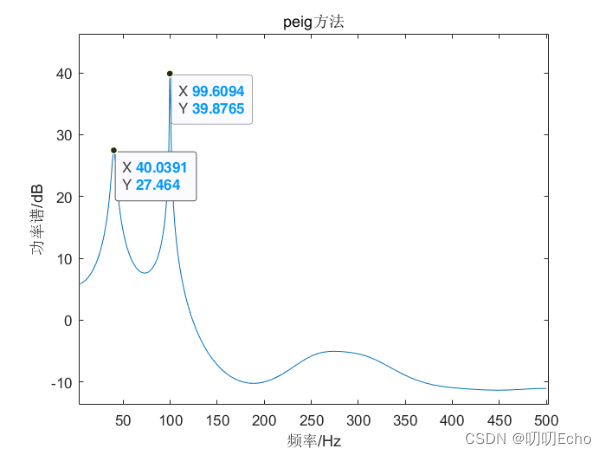
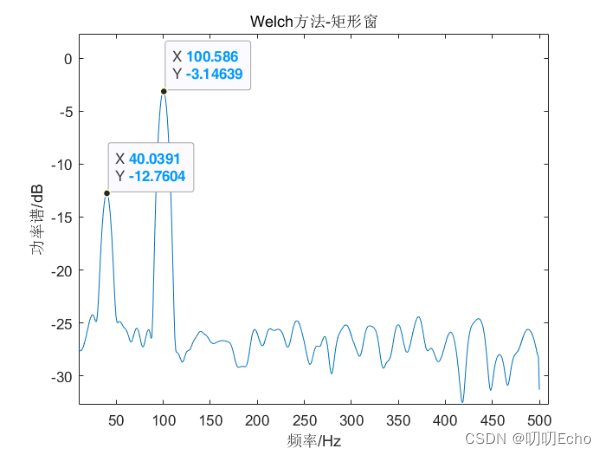
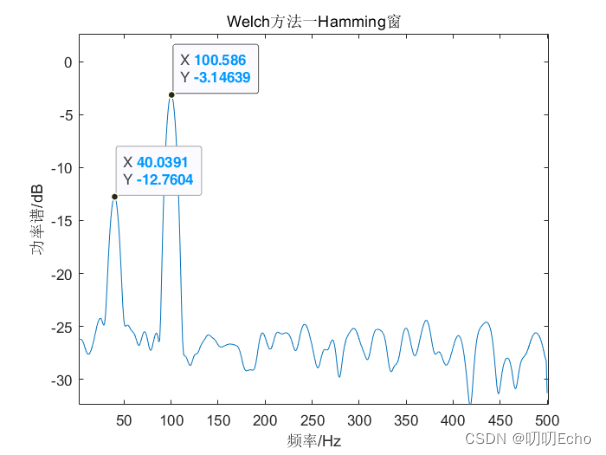
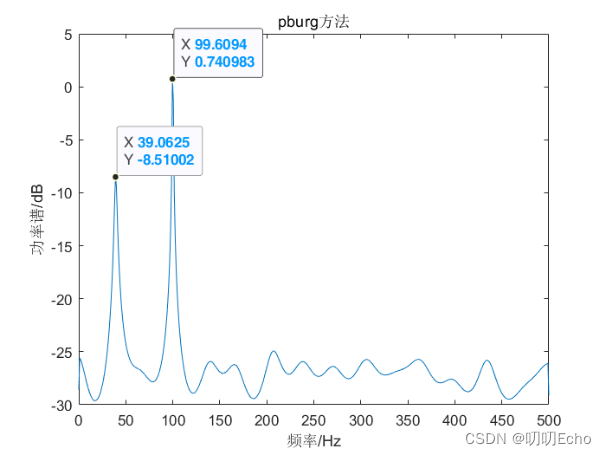
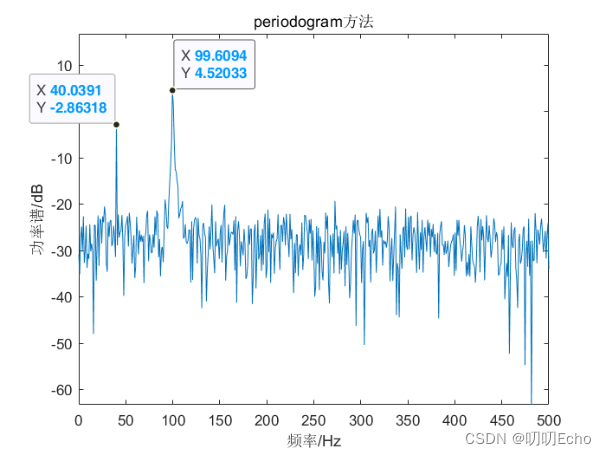
(二)频率分析结果
表1 频率分析结果
f/Hz
| 40 | 100 | 信号频率处 | 非频率处 | |
| pcov | 40.0391 | 99.6094 | 信号明显 | 波动小 |
| pmcov | 40.0391 | 99.6094 | 信号明显 | 波动小 |
| pyulear | 40.0391 | 99.6094 | 信号明显 | 波动小 |
| pmtm | 39.0625 | 101.563 | 信号明显 | 波动较小 |
| pmusic | 40.0391 | 99.6094 | 信号明显 | 波动圆滑 |
| peig | 40.0391 | 99.6094 | 信号明显 | 波动圆滑 |
| Pwelch-矩形窗 | 40.0391 | 100.586 | 信号明显 | 波动较大 |
| Pwelch-Hamming窗 | 40.0391 | 100.586 | 信号明显 | 波动较大 |
| pburg | 39.0625 | 99.6094 | 信号明显 | 波动较小 |
| periodogram | 40.0391 | 99.6094 | 信号明显 | 波动大 |
1)从谱图来看,各种功率谱的分析函数都能进行较好的分辨出来:
- pcov和pyulear谱图在信号频率处的谱线有一定的宽度且突出,其他地方的谱线有一定的起伏但不会很大,容易分辨出信号源频率;
- periodogram谱图在信号频率处的谱线宽度狭窄且突出,频率确定范围狭窄,较容易分辨出信号源频率,其他地方的谱线起伏剧烈波动大;
- Pmusic、peig谱图的谱线较为圆滑,在信号源频率处谱线峰值明显,容易分辨出信号源频率,但峰带频率跨度大;
- Pmtm和pwelch谱图在信号频率处的谱线宽度较为狭窄且突出,容易分辨出信号源频率,其他地方的谱线的起伏波动较为明显但起伏不会很大;
- pburg和pmcov谱图在信号频率处的谱线有一定的宽度且突出,容易分辨出信号源频率,其他地方的谱线有一定的宽度波动但起伏不大;
2)从matlabde的函数调用来看:
表2 函数
| 函数 | matlab函数表达式 | 参数个数 | 选参数难度 |
| pwelch-矩形窗 | [Pxx1,f]=pwelch(xn,[],noverlap,nfft,Fs,range); | 6 | 容易 |
| pwelch-Hamming窗 | [Pxx2,f]=pwelch(xn,[],noverlap,nfft,Fs,range); | 6 | 容易 |
| pcov | [Pxx3,f]=pcov(xn,20,nfft,Fs,range); | 5 | 难 |
| pmcov | [Pxx4,f]=pmcov(xn,35,nfft,Fs,range); | 5 | 难 |
| pyulear | [Pxx5,f]=pyulear(xn,35,nfft,Fs,range); | 5 | 难 |
| pmtm | [Pxx6,f]=pmtm(xn,5,nfft,Fs,range); | 5 | 难 |
| pmusic | [Pxx7,f]=pmusic(xn,6,nfft,Fs,range); | 5 | 难 |
| peig | [Pxx8,f]=peig(xn,6,nfft,Fs,range); | 5 | 难 |
| pburg | [Pxx9,f]=pburg(xn,30,nfft,Fs,range) | 5 | 难 |
| periodogram | [Pxx10,f]=periodogram(xn,[],nfft,Fs,range); | 5 | 容易 |
从函数的调用选择来看,参数个数而言,pwelch的参数个数为6, pcov, pmcov, pyulear, pmtm, pmusic, peig, pwelch, pburg 和periodogram的参数个数都为5;其中,pwelch和periodogram的参数选取容易,参数影响较小,能较好找到符合要求的参数。pcov, pmcov, pyulear, pmtm, pmusic, peig, pwelch和pburg的个别参数选择较难(如:pmtm功率谱的时宽带宽积,pmusic和peig的信号空间中特征向量的维数,pyulear、pcov和pmcov的AR模型阶数),参数选取影响较大。
特别说明,AR模型的参数计算目前的很多算法还无法在保持稳定性的前提下估计效果和计算速度方面明显占优,以Matlab为例,目前文献中所进行的参数估计都需要大量复杂的运算,并且需要充分掌握算法,对零基础的测试行业从业者很不友好。
三、小结
综上所述,pwelch函数是较为理想的函数,其实际信号功率谱估计分析较为直观明了,信号辨别容易,函数调用选取,参数选取比较容易,所以我认为选取pwelch进行分析。
以上仅代表个人观点,由于认识不深,如有考虑不足和欠缺之处,还望老师斧正!
参考文献:
[1]王福杰, 潘宏侠. MATLAB中几种功率谱估计函数的比较分析与选择[J]. 电子产品可靠性与环境试验, 2009, 27(6):4.
[2]解翔, 卫红凯, 马珂. 窗函数对传统功率谱估计精度的影响[J]. 船舶电子对抗, 2009, 32(2):3.
[3]何璇.基于Matlab的AR模型参数估计[J].信息与电脑(理论版),2019(07):5-6.
Matlab源码如下:
clc;
clear;
Fs=1000;
n=0:1/Fs:1;
xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n));
nfft=1024;
window=boxcar(100); %矩形窗
window1=hamming(100); % Harmming窗
noverlap=20; %数据无重叠
range='onesided'; %频率间隔为[0 Fs/2],只计算一半的频率
[Pxx1,f]=pwelch(xn,[],noverlap,nfft,Fs,range); %pwelch
[Pxx2,f]=pwelch(xn,[],noverlap,nfft,Fs,range); %pwelch
[Pxx3,f]=pcov(xn,20,nfft,Fs,range); %1.pcov
[Pxx4,f]=pmcov(xn,35,nfft,Fs,range); %2.pmcov
[Pxx5,f]=pyulear(xn,35,nfft,Fs,range); %3.pyulear
[Pxx6,f]=pmtm(xn,5,nfft,Fs,range); %4.pmtm
[Pxx7,f]=pmusic(xn,6,nfft,Fs,range); %5.pmusic
[Pxx8,f]=peig(xn,6,nfft,Fs,range); %6.peig
[Pxx9,f]=pburg(xn,30,nfft,Fs,range) %7.pburg
[Pxx10,f]=periodogram(xn,[],nfft,Fs,range); %8.periodogram
%[Pxx2,f]=arburg(xn,nfft); %9.arburg
%[Pxx2,f]=prony(xn,500,20); %10.prony
plot_Pxx1=10*log10(Pxx1); %将计算出的功率谱通过换算成分贝单位
plot_Pxx2=10*log10(Pxx2);
plot_Pxx3=10*log10(Pxx3);
plot_Pxx4=10*log10(Pxx4);
plot_Pxx5=10*log10(Pxx5);
plot_Pxx6=10*log10(Pxx6);
plot_Pxx7=10*log10(Pxx7);
plot_Pxx8=10*log10(Pxx8);
plot_Pxx9=10*log10(Pxx9);
plot_Pxx10=10*log10(Pxx10);
figure(1)
% subplot(2,2,1)
plot(f,plot_Pxx1);
title('Welch方法-矩形窗');
xlabel('频率/Hz' );ylabel('功率谱/dB');
% subplot(2,2,2)
figure(2)
plot(f,plot_Pxx2);
title('Welch方法一Hamming窗');
xlabel('频率/Hz' );ylabel('功率谱/dB');
% subplot(2,2,3)
figure(3)
plot(f,plot_Pxx3);
title('pcov方法');
xlabel('频率/Hz' );ylabel('功率谱/dB');
% subplot(2,2,4)
figure(4)
plot(f,plot_Pxx4);
title('pmcov方法');
xlabel('频率/Hz' );ylabel('功率谱/dB');
figure(5)
plot(f,plot_Pxx5);
title('pyulear方法');
xlabel('频率/Hz' );ylabel('功率谱/dB');
figure(6)
plot(f,plot_Pxx6);
title('pmtm方法');
xlabel('频率/Hz' );ylabel('功率谱/dB');
figure(7)
plot(f,plot_Pxx7);
title('pmusic方法');
xlabel('频率/Hz' );ylabel('功率谱/dB');
figure(8)
plot(f,plot_Pxx8);
title('peig方法');
xlabel('频率/Hz' );ylabel('功率谱/dB');
figure(9)
plot(f,plot_Pxx9);
title('pburg方法');
xlabel('频率/Hz' );ylabel('功率谱/dB');
figure(10)
plot(f,plot_Pxx10);
title('periodogram方法');
xlabel('频率/Hz' );ylabel('功率谱/dB'); 最后
以上就是开朗往事最近收集整理的关于故障诊断作业2的全部内容,更多相关故障诊断作业2内容请搜索靠谱客的其他文章。





![matlab periodgram,[转载]matlab中[Pxx,f] = periodogram(x,window,nfft,fs)](https://www.shuijiaxian.com/files_image/reation/bcimg3.png)


发表评论 取消回复