Pytorch的官网链接https://pytorch.org/tutorials/beginner/pytorch_with_examples.html#id12

数组和张量的区别

数组Numpy可以建立n维数组，但是numpy数组并不能用于计算图(computation graphs)、深度学习、求梯度等等。并且Numpy不能使用GPU资源，加快计算速度。现代深度神经网络计算过程中如果用到了GPU资源，可以把计算速度提升50倍甚至更高，显然仅使用numpy是不能满足需求的。

Pytorch中最基本的概念：张量tensor
张量的形式类似于Numpy，一个张量就是一个n维的数组，pytorch中也提供了一些可以操作计算这些张量的函数。
除此之外，tensor可以用于图计算和梯度计算。
并且tensor可以使用GPU资源

计算图

参考博客链接地址这个博客内容来源于李宏毅深度学习的内容。

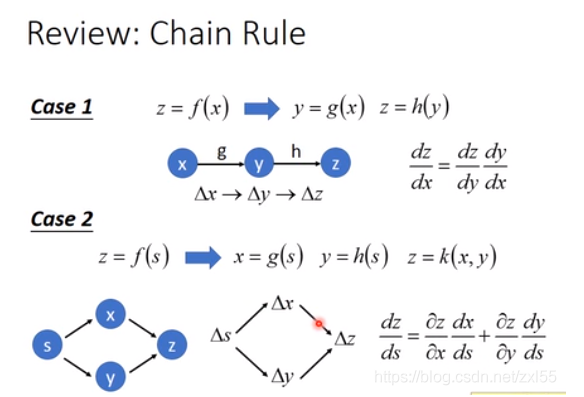
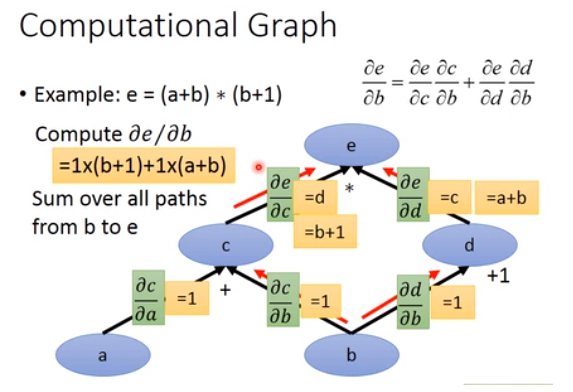
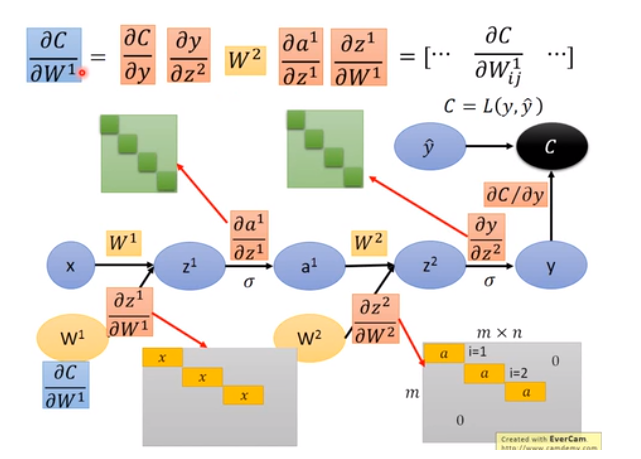
torch中创建变量

torch.empty()创建未初始化的tensor

torch.empty(2,3)#产生2*3维的tensor，它是未初始化的，
#可以无穷大也可以无穷小，
#大概可以理解为建立了一个这种形状的tensor吧，值不重要。

随机初始化的矩阵

类似于numpy的随机数，只是把numpy换成torch

#创建2*3维的tensor
torch.rand(2,3) #[0,1]均匀分布
torch.randint(1,100,[2,3])  #[1,100)区间内整数
torch.randn(2,3) #标准正态

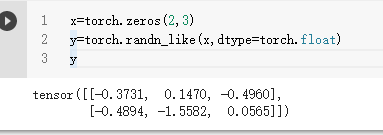
torch.zeros()全0的tensor

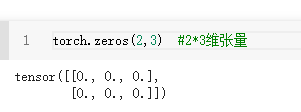
手动设置tensor中元素的数据类型

整型一般分为以下三种。

浮点数有float和double

从数据直接构建tensor

x=torch.tensor([4,5,6])
x

创建与已有tensor有相同数据类型的新tensor

y=x.new_ones(5,3)
#创建5*3维的tensor
#这个tensor中每个元素都是1
#tensor中每个元素的数据类型dtype都与x中元素数据类型相同

随机产生与已有tensor有相同形状的新tensor

将tensor在cpu和GPU上移动

注意，这种移动是有必要的。
比如从GPU到cpu，因为numpy模块只能在cpu上做运算，如果tensor没有取回cpu就不能用numpy中的函数。

x.to('cuda') #GPU使用的英伟达GPU，用cuda表示，不能直接写GPU
x.cuda()

y.to('cpu')
y.cpu()

使用pytorch时，设立随机种子

参考博客链接地址。

def seed_torch(seed=1029):
	random.seed(seed) #python设置随机数
	os.environ['PYTHONHASHSEED'] = str(seed) 
	# 为了禁止hash随机化，使得实验可复现
	np.random.seed(seed) #numpy设置随机数
	torch.manual_seed(seed) #给cpu设置种子
	torch.cuda.manual_seed(seed) #给GPU设置种子
	torch.cuda.manual_seed_all(seed)
	 #if you are using multi-GPU.，给多个GPU设置种子
	 #给torch设置随机数
	torch.backends.cudnn.benchmark = False
	torch.backends.cudnn.deterministic = True

seed_torch()

pytorch里面不同于numpy的函数

import torch
x=torch.randn(2,3)#产生2*3维的服从标准正态分布的张量
x.mm(y) #矩阵的叉乘，同线性代数
x.clamp(min=0)#求Relu函数值，x>0是取值为x，x<=0时取值为0
x.clamp(min=2,max=6)#x<2则为2，x>6则为6，x在[2,6]内则为x
x.pow(2)#求幂，也即x^2
x.item()#若张量x中只有一个元素，可以用.item将它取出为普通数字
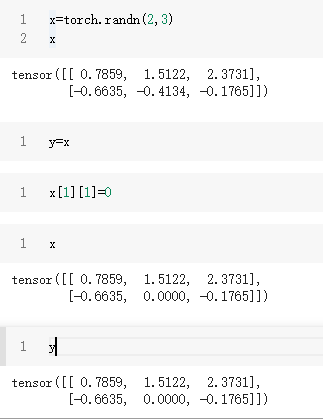
x_new=x.clone()#将张量复制给一个新的张量，这样就不会公用内存
#如果直接用x_new=x则一旦修改x，则x_new也会改变。它俩地址相同
#numpy中也有类似用法x_new=x.copy(),不共用内存

x.t() #矩阵转置

创建带有grad结构的tensor

• 直接创建tensor时的函数后面加上参数requires_grad=True。

这样在创建tensor时就会分配给它一个空间，存储tensor的梯度grad。tensor中能够有grad属性，这是tensor与numpy的一大区别，这就造成了，tensor用于计算图并自动计算梯度，而numpy不行。

x=torch.randn(3,requires_grad=True)

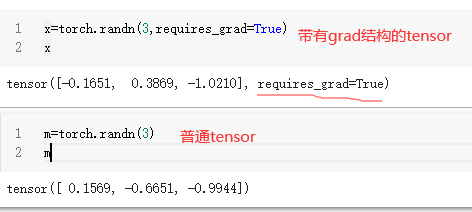
• 给现有的tensor添加grad结构
  

leaf叶张量(.is_leaf)

在创建torch.Tensor时，如果没有人为设定requires_grad这个参数，默认的是requires_grad=False，也即不给tensor这个grad的属性。
叶张量：
①凡是requires_grad=False的张量都是叶张量。不管它们做什么运算（加、减、乘、除、从cpu映射到cuda等等），仍然是叶张量。
②凡是人为手动设定requires_grad=True的张量都是叶张量，利用.requires_grad_()也是相同。
③requires_grad=True的张量，一旦进行一点运算（加、减、乘、除、从cpu映射到cuda）都会变成grad_fn，这意味着它们是运算的结果,它们也不再是叶张量。换句话来说，这个新张量是由前一个张量运算得来的，在计算图中新张量就不是叶子节点了。
注意：
只有叶张量，并且叶张量有grad结构才能在backforward中自动求梯度"x.grad"

• 没有grad结构的张量及其运算
  
• 有grad结构的张量及其运算
  

带grad结构的tensor直接运算

直接对带有grad结构的tensor做简单的数学运算时，新产生的变量仍然是tensor，但是新tensor中的grad结构已经被破坏了，变成grad_fn乱码。

y=x+1
print(x)
print(y) #grad结构被破坏了
y.is_leaf

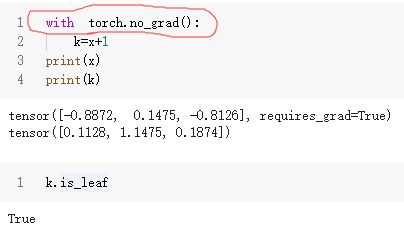
利用with torch.no_grad():对带有grad的张量进行运算

注意：如果直接对带grad结构的tensor直接运算，那么这个tensor就不再是叶子节点了，同时也会有graf_fn的杂乱内容
如果想要对带grad结构的tensor进行运算，但是又不想改变它的grad结构以及叶张量的属性，那么可以用with torch.no_grad():将运算包裹起来。

with torch.no_grad():
  k=x+1
print(x)
print(k)
k.is_leaf

迭代过程中w.grad的特点【w.grad.zero_()】

• 第一张图

• 第二张图

第二张图中x,y,w1,w2的tensor具体元素是没有改变的，只是w1中的grad结构已经有值了，它不是空的，w2同理。
然后做同样的计算，我们会发现，这时经过backforward之后，w1.grad的值比第一张图要大，这其实是，新得到一个grad值之后加在了已有的grad值上面。第一张图是首次计算w1.grad，这个是正确的结果，注意到（第一张图）w1.grad=9572.6582；还可以注意到(第二张图）w1.grad=19145.3164=9572.6582+9572.6582，这个值其实是根据x,y，w1,w2计算得到的grad值的两倍，如果再次重复运算第二张图，那么grad值会变成正确答案的三倍。
总结：
如果在backforward之前，张量的grad结构中是有值的，也即它非空，那么“backforward中求得的梯度grad(正确值)”就会加在grad结构初始值上。与初始值相加之后的结果并不是我们想要的。
所以，在backforward之前一定要把所有需要求w.grad的张量w都变为空，或者变成元素全0。
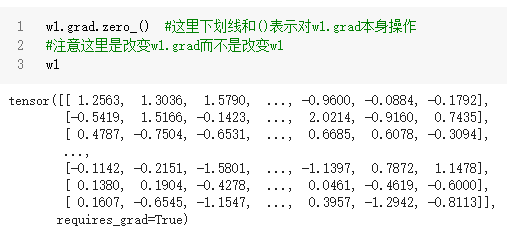
这里w1.grad.zero_()是改变w1.grad，就是改了w1的grad结构中的值，对w1本身并没有影响，它还是叶张量，且requires_grad=True
w1.grad只是一个普通的tensor

w1.grad.zero_()

torch中的自带的网络结构模块torch.nn

参考torch.nn的官网介绍链接地址
可以直接用torch.nn建立神经网络的每一层，然后层层叠加即可，不用再自己手动定义参数，然后计算forward结果。

构建模型torch.nn.Sequential

# 每层结构按顺序累加，用逗号隔开
model = torch.nn.Sequential(
    torch.nn.Linear(D_in, H), #w_1*x+b
    torch.nn.ReLU(),          #ReLU激活函数
    torch.nn.Linear(H, D_out), #w_2*h+b
)

#求神经网络预测值，自动执行forward计算
y_pred = model(x)

• 查看模型的信息

模型中参数的初始化(w_1,b_1,w_2…)

这里使用torch.nn建立神经网络模型时，它的参数$w_1$、$b_1$、$w_2$、$b_2$的初始化是它自己在内部初始化地，不是显式的，也不需要自己手动设置初始化值，一般情况下默认选择torch.nn.init.kaimin_uniform_()或者torch.nn.init.kaiming_normal_()。
但是模型初始化的值的好坏有时候会对模型造成影响，偶尔模型本身给出的初始化值，计算得到的模型预测结果并不很好，所以这时可以手动更改参数初始值，尝试一下。

#初始化为标准正态分布
#torch.nn.init.normal_(tensor, mean=0.0, std=1.0)
torch.nn.init.norm_(model[0].weight)
torch.nn.init.norm_(model[0].bias)
#初始化为[0,1]均匀分布
#torch.nn.init.uniform_(tensor, a=0.0, b=1.0)
torch.nn.init.uniform_(model[0].weight)

torch.nn中求最终的损失函数

torch.nn.MSELoss(xtensor,ytensor,reduction="mean")
#这里函数前两个参数，是张量的位置
#重要考虑reduction参数

reduction=‘mean’，结果为$\frac{1}{n}{\sum }_{i=1}^n(x_i-y_i{)}^2$
reduction=‘sum’，结果为${\sum }_{i=1}^n(x_i-y_i{)}^2$
reduction=‘none’，结果为张量，每个对应位置元素为$(x_i-y_i{)}^2$
注意：
这里xtensor和ytensor都是张量，可以是多维，也可以多维，它们的形状相同，然后都有n个元素。

import torch.nn
loss_fn=torch.nn.MSELoss(reduction='sum') #定义损失函数
x=torch.randn(3,5)
y=torch.randn(3,5)
loss_fn(x,y)

torch.nn中给参数grad结构清零

model.zero_grad()

torch.nn中参数更新

• 简单梯度下降法更新

with torch.no_grad():
    for param in model.parameters():
        param -= learning_rate * param.grad
#这里的model.parameters()是模型中所有参数，
#如，w_1,b_1,w_2,b_2等等

• 采用torch.optim()优化器进行参数更新

#这两句相当于引用一个优化器Adam，并给定参数
#Adam适合默认的kaiming初始化参数
learning_rate=1e-4 #或者1e-3,比较适合Adam优化器
optimizer=torch.optim.Adam(model.parameters(),lr=learning_rate)
#优化器也可以为SGD，适合手动Normal初始化参数
learning_rate=1e-6
optimizer=torch.optim.SGD(model.parametes(),lr=learning_rate)

#利用优化器给grad结构清零
optimizer.zero_grad()

#利用优化器更新参数，相当于之前with结构体下的内容
optimizer.step()

层结构

Linear Layers

#隐含层或输出层结构的表示方法，不考虑输入层
torch.nn.Linear(in节点数, out节点数, bias=True)
#bias默认是True，即默认存在偏差b

激活函数

ReLU激活函数

torch.nn.ReLU() 

Sigmoid激活函数

torch.nn.Sigmoid()

Tanh激活函数

torch.nn.Tanh()

查看torch使用的GPU的信息

这里Google Colab上面只提供Tesla T4类型的GPU，然后免费版也只有一个GPU资源可以使用。

torch中帮助文档

• 可以利用代码实现

#比如要查询.is_leaf这个函数的意义
import torch
help(torch.Tensor.is_leaf)

• 可以直接在torch的官方网站中文档界面搜索

https://pytorch.org/docs/stable/search.html?q=is_leaf&check_keywords=yes&area=default#

参考资料

常用激活函数求导
ReLU函数详解及反向传播中的梯度求导
B站褚博士讲解视频

最后

以上就是孤独大米为你收集整理的Pytorch入门(一)数组和张量的区别计算图torch中创建变量使用pytorch时，设立随机种子pytorch里面不同于numpy的函数torch中的自带的网络结构模块torch.nn查看torch使用的GPU的信息torch中帮助文档参考资料的全部内容，希望文章能够帮你解决Pytorch入门(一)数组和张量的区别计算图torch中创建变量使用pytorch时，设立随机种子pytorch里面不同于numpy的函数torch中的自带的网络结构模块torch.nn查看torch使用的GPU的信息torch中帮助文档参考资料所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。