TF乘法之multiply、matmul、*

69 阅读 0 评论 46 点赞

我是靠谱客的博主威武缘分，最近开发中收集的这篇文章主要介绍TF乘法之multiply、matmul、*，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

在这里插入图片描述

"*"和tf.multiply 属于元素级别的相乘，两个矩阵或者向量维度一直，对应位置相乘维度保持不变
multiply(x,y,name=None)—实现元素级别的相乘
1）注意：x与y要有相同的数据类型，要是int都是int，要是float都是float 否则会报错
2）若y为数，x为向量或矩阵，则用y乘以x中的每一个元素：

x2 = tf.constant([[1.0, 1.1, 1.2], [1.3, 1.4, 1.5], [1.6, 1.7, 1.8]])
y2 = tf.constant(2.0)#这里的值同样需要是float型，若是int型，则会报错
z2 = tf.multiply(x2, y2)

结果为：[[ 2. 2.20000005 2.4000001 ]
[ 2.5999999 2.79999995 3. ]
[ 3.20000005 3.4000001 3.5999999 ]]
3) 若y为向量，x为矩阵，则必须满足：若y是行向量，则元素个数应与x的行数相等；若y是列向量，则需与x的列数相等：

x2 = tf.constant([[1.0, 2.0, 3.0], [1.0, 2.0, 3.0], [1.0, 2.0, 3.0], [1.0, 2.0, 3.0]])  # 4*3
y2 = tf.constant([1.0, 1, 2])  # 1*3
z2 = tf.multiply(x2, y2) # 等价于 z2= x2*y2
print("列元素一直自动复制行维度与相乘矩阵保持一致:", z2)

y3 = tf.constant([[1.0], [1], [2], [3]])  # 4*1
z3 = tf.multiply(x2, y2)# 等价于 z3 = y3 * z3
print("行元素一直自动复制列维度与相乘矩阵保持一致:", z3)

列元素一直自动复制行维度与相乘矩阵保持一致: tf.Tensor(
[[1. 2. 6.]
[1. 2. 6.]
[1. 2. 6.]
[1. 2. 6.]], shape=(4, 3), dtype=float32) tf.Tensor(
[[1. 2. 6.]
[1. 2. 6.]
[1. 2. 6.]
[1. 2. 6.]], shape=(4, 3), dtype=float32)
行元素一直自动复制列维度与相乘矩阵保持一致: tf.Tensor(
[[1. 2. 6.]
[1. 2. 6.]
[1. 2. 6.]
[1. 2. 6.]], shape=(4, 3), dtype=float32) tf.Tensor(
[[ 1. 2. 6.]
[ 1. 2. 6.]
[ 2. 4. 12.]
[ 3. 6. 18.]], shape=(4, 3), dtype=float32)

#coding=utf-8
import  tensorflow as tf
if __name__ == '__main__':
    a = tf.constant([1 ,2, 3])
    b = tf.constant([2 ,3, 4])
    res_ab = a*b
    print("res_ab", res_ab)
    m_a = tf.constant([[1 ,2, 3],
                       [1, 2, 3]])
    m_b = tf.constant([[2, 3, 4],
                       [2, 3, 4]])
    res_mab = m_a * m_b
    print("res_mab", res_mab)

tf.matmul 符合数学上一般矩阵乘法的定义，注意matmul 对多维矩阵就是最后两个维度进行变换相乘

#coding=utf-8
import  tensorflow as tf

if __name__ == '__main__':
    print("--------------matmul-------------------")
    m_a = tf.constant([[1 ,2, 3],
                       [1, 2, 3]])
    m_b = tf.constant([[2, 3, 4],
                       [2, 3, 4]])
    mult_res = tf.matmul(m_a, m_b, transpose_b=True)
    print("mult_res:",mult_res)

MultiHeadAttention 实现代码

q = self.wq(q)  # (batch_size, seq_len, d_model)
k = self.wk(k)  # (batch_size, seq_len, d_model)
v = self.wv(v)  # (batch_size, seq_len, d_model)

q = self.split_heads(q, batch_size)  # (batch_size, num_heads, seq_len_q, depth)
k = self.split_heads(k, batch_size)  # (batch_size, num_heads, seq_len_k, depth)
v = self.split_heads(v, batch_size)  # (batch_size, num_heads, seq_len_v, depth)

# scaled_attention.shape == (batch_size, num_heads, seq_len_q, depth)
# attention_weights.shape == (batch_size, num_heads, seq_len_q, seq_len_k)
scaled_attention, attention_weights = scaled_dot_product_attention(
    q, k, v, mask)

按照论文中的思路需要计算多个head 的scale dot product attention，再将attention_weight与计算结果，再concat，基本按照普通的实现方式就是串行执行
但是利用矩阵变换及矩阵相乘的并行计算，现在将x的embedding通过fc 映射成一个 head**depth长度的向量，然后进行拆解成将[batch, seq_len, num_head, depth]的向量，然后调整成 scale_dot_product_attetion 可以处理的维度，qkv均这样处理，然后进行attention计算，得到最终结果[batch,_size, num_head, seq_length, depth]，再进行一次维度变化，去掉num_head这一维，depth变化为num_head*depth

# 缩放点积注意力
def scaled_dot_product_attention(q ,k ,v ,mask):
    '''
    Args:
    -q : shape==(...,seq_len_q,depth)
    -k : shape==(...,seq_len_k,depth)
    -v : shape==(...,seq_len_v,depth_v)
    - seq_len_k = seq_len_v
    - mask: shape == (...,seq_len_q,seq_len_k) 点积
    return:
    output:weighted sum
    attention_weights:weights of attention
    '''
    # shape == (...,seq_len_q,seq_len_k)
    # embedding 向量算法内积
    # 矩阵乘法的最后一维进行相乘，其他模块基本不动
    matmul_qk =tf.matmul(q, k, transpose_b=True)
    dk = tf.cast(tf.shape(k)[-1], tf.float32)
    scaled_attention_logits = matmul_qk / tf.math.sqrt(dk)
    if mask is not None:
        # 10的负九次方比较大，会使得需要掩盖的数据在softmax的时候趋近0
        scaled_attention_logits += (mask * -1e9)
    # shape == (...,seq_len_q,seq_len_k)
    attention_weights = tf.nn.softmax(scaled_attention_logits, axis=-1)
    # shape==(...,seq_len_q,depth_v)
    output = tf.matmul(attention_weights, v)
    return output, attention_weights


def print_scaled_dot_attention(q, k, v):
    temp_out, temp_att = scaled_dot_product_attention(q, k, v, None)
    print("Attention weights are:")
    print(temp_att)
    print("Outputs are:")
    print(temp_out)

从scale_dot_product_attetion 体会到的矩阵乘法的向量乘法意义：

weight = tf.constant([[1, 2, 3, 1], [4, 5, 6, 1], [7, 8, 9, 1]], dtype=tf.float32) # (3 ,4)
value = tf.constant([[1, 1, 1], [1, 1, 1], [1, 1, 1], [1, 1, 1]], dtype=tf.float32) # (4, 3)
weight_value =tf.matmul(weight, value)
print(matmul_qk)

tf.Tensor(
[[ 7. 7. 7.]
[16. 16. 16.]
[25. 25. 25.]], shape=(3, 3), dtype=float32)

weight向量（3，4）与 value (4,3)向量进行矩阵乘法
从直观意义上讲是对 value 每个行向量进行加权求和，weight列的序号，对应 value行向量序号，然后让对应单个值与一个向量进行相乘，在讲4列整体累加，这个符合矩阵乘法的几何意义。
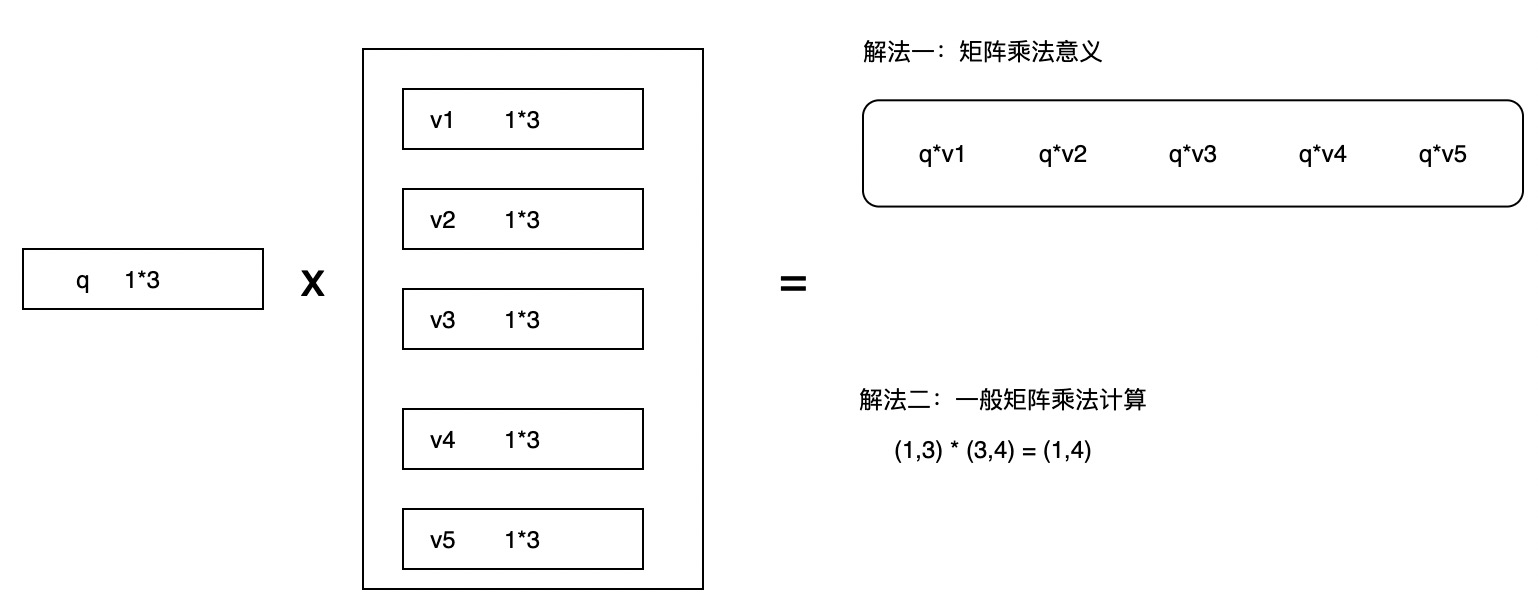
在这里插入图片描述

这个是权重计算原理

还有一个是scale_dot_product
scale 是指softmax
dot_product指的是点积计算权重
两个矩阵相乘，其实计算的这个行向量和每一个列向量的相关性，需要注意一点 q向量不需要转置，k向量需要在mutli前进行转置

import tensorflow as tf

w = tf.Variable([[0.4], [1.2]], dtype=tf.float32) # w.shape: [2, 1]
x = tf.Variable([range(1,6), range(5,10)], dtype=tf.float32) # x.shape: [2, 5]
y = w * x     # 等同于 y = tf.multiply(w, x)   y.shape: [2, 5]

sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)

print sess.run(w)
print sess.run(x)
print sess.run(y)

Python 之 numpy 和 tensorflow 中的各种乘法（点乘和矩阵乘）
https://blog.csdn.net/weixin_45459911/article/details/107852351
Tensorflow函数学习笔记2—tf.multipy和tf.matmul
tf中multiply、matmul、dot、batch_dot区别