np.random.rand/newaxis/tf.multiply与tf.matmul的区别/tf.reduce_sum()函数和tf.reduce_mean()函数np.random.rand(d0,d1,d2……dn)newaxistf.multiply与tf.matmul的区别tf.reduce_sum()函数和tf.reduce_mean()函数Reference

63 阅读 0 评论 42 点赞

我是靠谱客的博主专注柚子，最近开发中收集的这篇文章主要介绍np.random.rand/newaxis/tf.multiply与tf.matmul的区别/tf.reduce_sum()函数和tf.reduce_mean()函数np.random.rand(d0,d1,d2……dn)newaxistf.multiply与tf.matmul的区别tf.reduce_sum()函数和tf.reduce_mean()函数Reference，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

np.random.rand(d0,d1,d2……dn)

通过本函数可以返回一个或一组服从“0~1”均匀分布的随机样本值。随机样本取值范围是[0,1)，不包括1。
1)当函数括号内没有参数时，则返回一个浮点数；
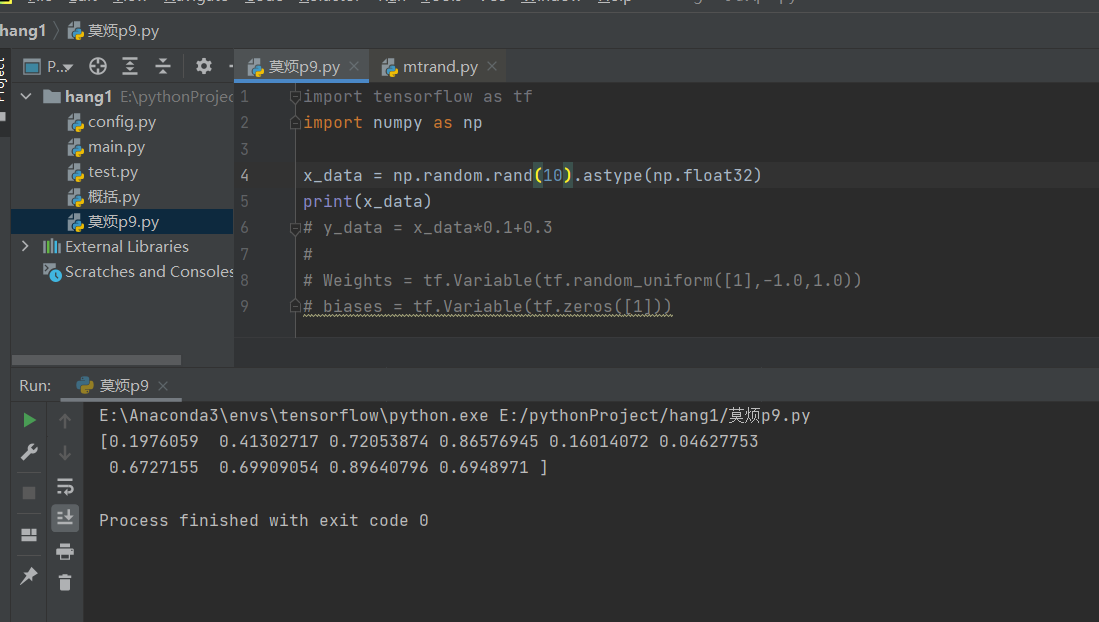
2）当函数括号内有一个参数时，则返回秩为1的数组，不能表示向量和矩阵；
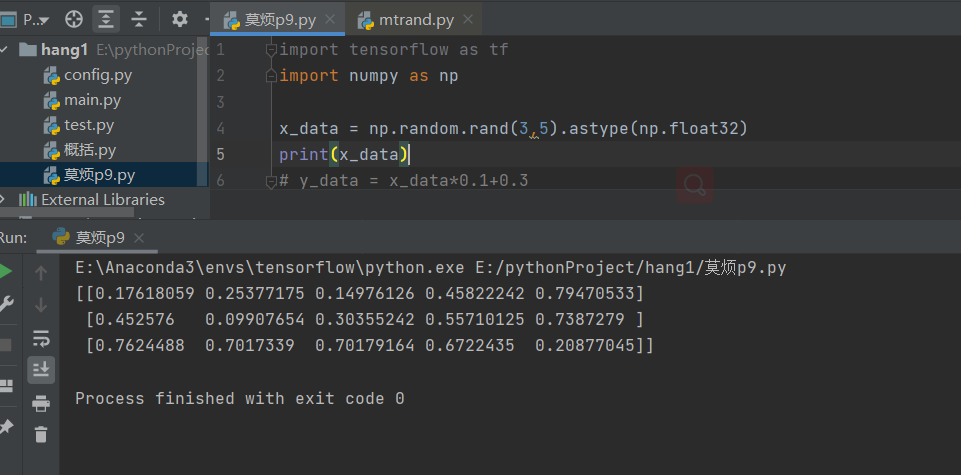
3）当函数括号内有两个及以上参数时，则返回对应维度的数组，能表示向量或矩阵；

newaxis

运行如下代码：
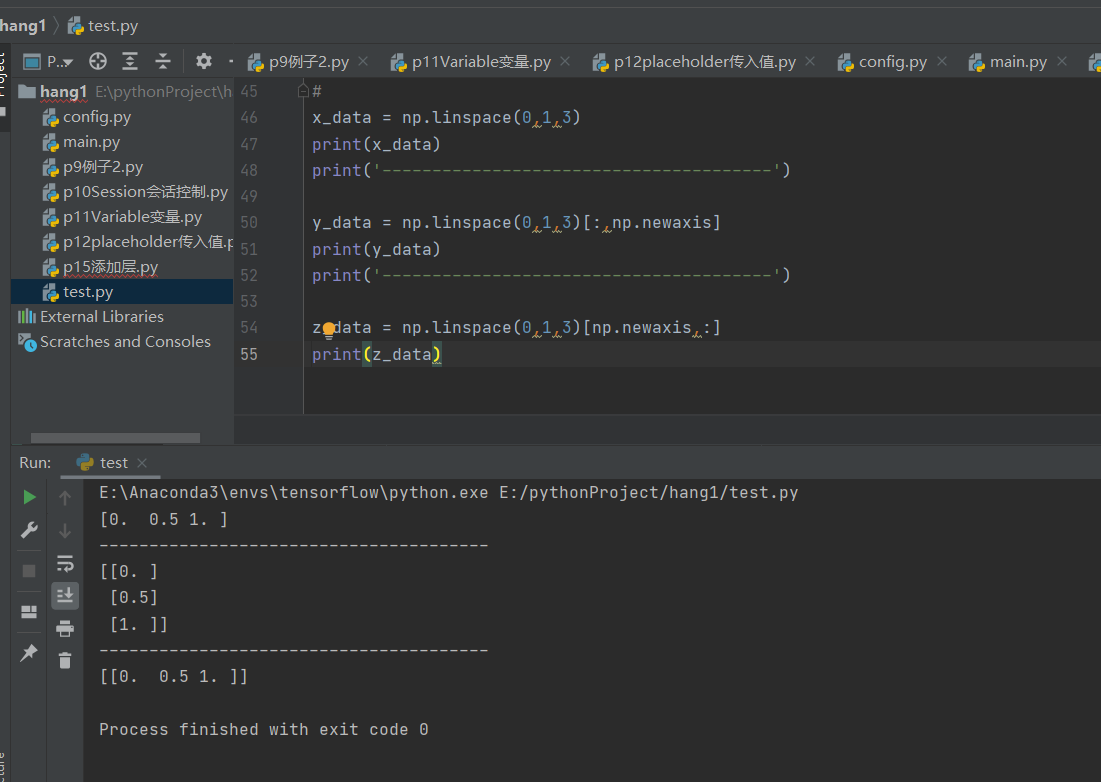
在这里插入图片描述

由以上代码可以看出，以前的shape是3
把newaxis放后面的时候，输出的新数组的shape就是3××1，也就是后面增加了一个维数newaxis
把newaxis放在前面的时候变成了1××3，也就是前面的维数增加了一个
newaxis放在第几个位置，就会在shape里面看到相应的位置增加了一个维数

tf.multiply与tf.matmul的区别

tf.multiply（）可用作两个矩阵中对应元素各自相乘等
tf.matmul（）将矩阵a乘以矩阵b，生成a * b
tf.multiply不一定是逐个元素对应相乘，也可能是利用广播特性。

tf.multiply（）

import tensorflow as tf

#两个矩阵的对应元素各自相乘！！
x=tf.constant([[1.0,2.0,3.0],[1.0,2.0,3.0],[1.0,2.0,3.0]])
y=tf.constant([[0,0,1.0],[0,0,1.0],[0,0,1.0]])
#注意这里这里x,y要有相同的数据类型，不然就会因为数据类型不匹配而出错
z=tf.multiply(x,y)

#两个数相乘
x1=tf.constant(1)
y1=tf.constant(2)
#注意这里这里x1,y1要有相同的数据类型，不然就会因为数据类型不匹配而出错
z1=tf.multiply(x1,y1)

#数和矩阵相乘
x2=tf.constant([[1.0,2.0,3.0],[1.0,2.0,3.0],[1.0,2.0,3.0]])
y2=tf.constant(2.0)
#注意这里这里x1,y1要有相同的数据类型，不然就会因为数据类型不匹配而出错
z2=tf.multiply(x2,y2)
with tf.Session() as sess:
    print(sess.run(z))
    print(sess.run(z1))
    print(sess.run(z2))

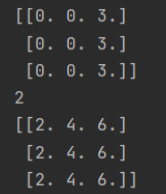
在这里插入图片描述

tf.matmul（）

#两个矩阵相乘
x3=tf.constant([[1.0,2.0,3.0],[1.0,2.0,3.0],[1.0,2.0,3.0]])
y3=tf.constant([[0,0,1.0],[0,0,1.0],[0,0,1.0]])
#注意这里这里x,y要满足矩阵相乘的格式要求。
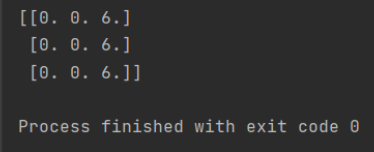
z3=tf.matmul(x,y)

with tf.Session() as sess:
    print(sess.run(z3))

在这里插入图片描述

tf.reduce_sum()函数和tf.reduce_mean()函数

tf.reduce_sum()

tf.reduce_sum
matrix1 = [[1.,2.,3.],            #二维，元素为列表
          [4.,5.,6.]]
matrix2 = [[[1.,2.],[3.,4.]],      #三维，元素为矩阵
           [[5.,6.],[7.,8.]]]

res_2 = tf.reduce_sum(matrix1)
res_3 = tf.reduce_sum(matrix2)
res1_2 = tf.reduce_sum(matrix1,reduction_indices=[0])
res1_3 = tf.reduce_sum(matrix2,reduction_indices=[0])
res2_2 = tf.reduce_sum(matrix1,reduction_indices=[1])
res2_3 = tf.reduce_sum(matrix2,reduction_indices=[1])

sess = tf.Session()
print("reduction_indices=None：res_2={}，res_3={}".format(sess.run(res_2),sess.run(res_3)))
print("reduction_indices=[0]：res1_2={}，res1_3={}".format(sess.run(res1_2),sess.run(res1_3)))
print("reduction_indices=[1]：res2_2={}，res2_3={}".format(sess.run(res2_2),sess.run(res2_3)))

result:

axis=None：res_2=21.0，res_3=36.0
axis=[0]：res1_2=[5. 7. 9.]，res1_3=[[ 6.  8.]
                                    [10. 12.]]
axis=[1]：res2_2=[ 6. 15.]，res2_3=[[ 4.  6.]
                                   [12. 14.]]

tf.reduce_mean
只需要把上面代码的reduce_sum部分换成renduce_mean即可

res_2 = tf.reduce_mean(matrix1)
res_3 = tf.reduce_mean(matrix2)
res1_2 = tf.reduce_mean(matrix1,axis=[0])
res1_3 = tf.reduce_mean(matrix2,axis=[0])
res2_2 = tf.reduce_mean(matrix1,axis=[1])
res2_3 = tf.reduce_mean(matrix2,axis=[1])

result:

axis=None：res_2=3.5，res_3=4.5
axis=[0]：res1_2=[2.5 3.5 4.5]，res1_3=[[3. 4.]
                                       [5. 6.]]
axis=[1]：res2_2=[2. 5.]，res2_3=[[2. 3.]
                                 [6. 7.]]

可以看到，reduction_indices和axis其实都是代表维度，当为None时，reduce_sum和reduce_mean对所有元素进行操作，当为[0]时，其实就是按行操作，当为[1]时，就是按列操作，对于三维情况，把最里面的括号当成是一个数，这样就可以用二维的情况代替，最后得到的结果都是在原来的基础上降一维，