1. 首页
  2. 文章中心
  3. 数据结构学习

第7章 集合和映射7-1 集合基础和基于二分搜索树的集合实现7-2 基于链表的集合实现7-3 集合类的复杂度分析7-4 LeetCode中的集合问题7-5 映射基础7-6 基于链表的映射实现7-7 基于二分搜索树的映射实现7-8 映射的复杂度分析7-9 LeetCode上更多集合和映射的问题

112 阅读 0 评论
我是靠谱客的博主 稳重河马，这篇文章主要介绍第7章 集合和映射7-1 集合基础和基于二分搜索树的集合实现7-2 基于链表的集合实现7-3 集合类的复杂度分析7-4 LeetCode中的集合问题7-5 映射基础7-6 基于链表的映射实现7-7 基于二分搜索树的映射实现7-8 映射的复杂度分析7-9 LeetCode上更多集合和映射的问题，现在分享给大家，希望可以做个参考。

第7章 集合和映射

  • 7-1 集合基础和基于二分搜索树的集合实现
  • 7-2 基于链表的集合实现
  • 7-3 集合类的复杂度分析
  • 7-4 LeetCode中的集合问题
  • 7-5 映射基础
  • 7-6 基于链表的映射实现
  • 7-7 基于二分搜索树的映射实现
  • 7-8 映射的复杂度分析
  • 7-9 LeetCode上更多集合和映射的问题

7-1 集合基础和基于二分搜索树的集合实现

在这里插入图片描述

复制代码
1
2
3
4
5
6
7
8
9
public interface Set<E> {

    void add(E e);
    boolean contains(E e);
    void remove(E e);
    int getSize();
    boolean isEmpty();
}

利用上一章实现的二分搜索树

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public class BSTSet<E extends Comparable<E>> implements Set<E> {

    private BST<E> bst;

    public BSTSet(){
        bst = new BST<>();
    }

    @Override
    public int getSize(){
        return bst.size();
    }

    @Override
    public boolean isEmpty(){
        return bst.isEmpty();
    }

    @Override
    public void add(E e){
        bst.add(e);
    }

    @Override
    public boolean contains(E e){
        return bst.contains(e);
    }

    @Override
    public void remove(E e){
        bst.remove(e);
    }
}

7-2 基于链表的集合实现

在这里插入图片描述

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import java.util.ArrayList;

public class LinkedListSet<E> implements Set<E> {

    private LinkedList<E> list;

    public LinkedListSet(){
        list = new LinkedList<>();
    }

    @Override
    public int getSize(){
        return list.getSize();
    }

    @Override
    public boolean isEmpty(){
        return list.isEmpty();
    }

    @Override
    public void add(E e){
        if(!list.contains(e))
            list.addFirst(e);
    }

    @Override
    public boolean contains(E e){
        return list.contains(e);
    }

    @Override
    public void remove(E e){
        list.removeElement(e);
    }
}

7-3 集合类的复杂度分析

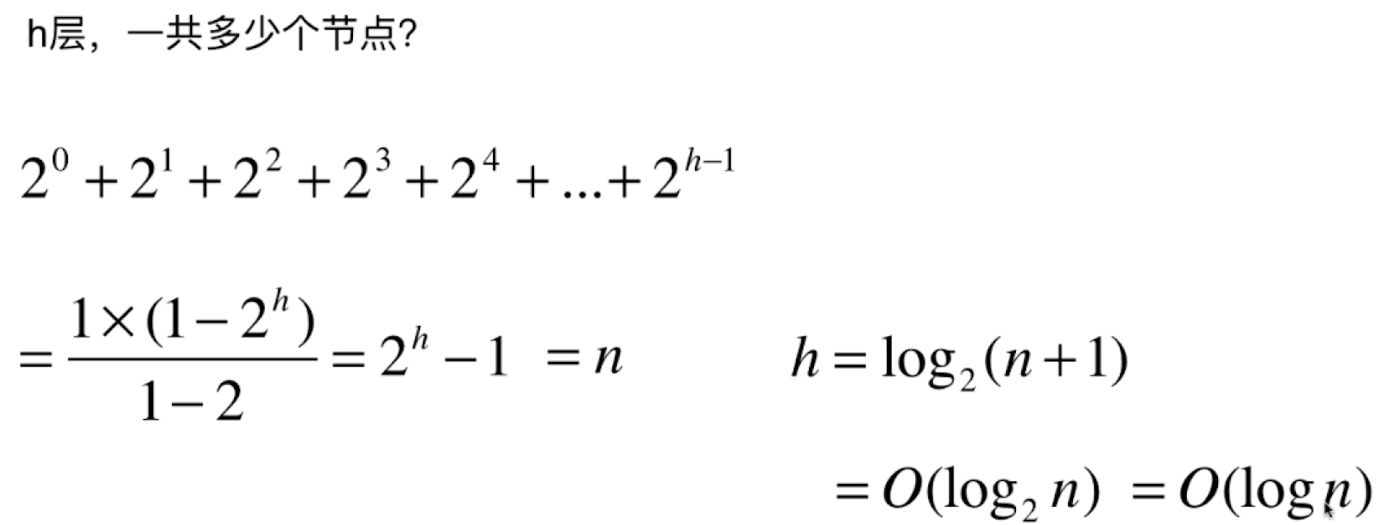
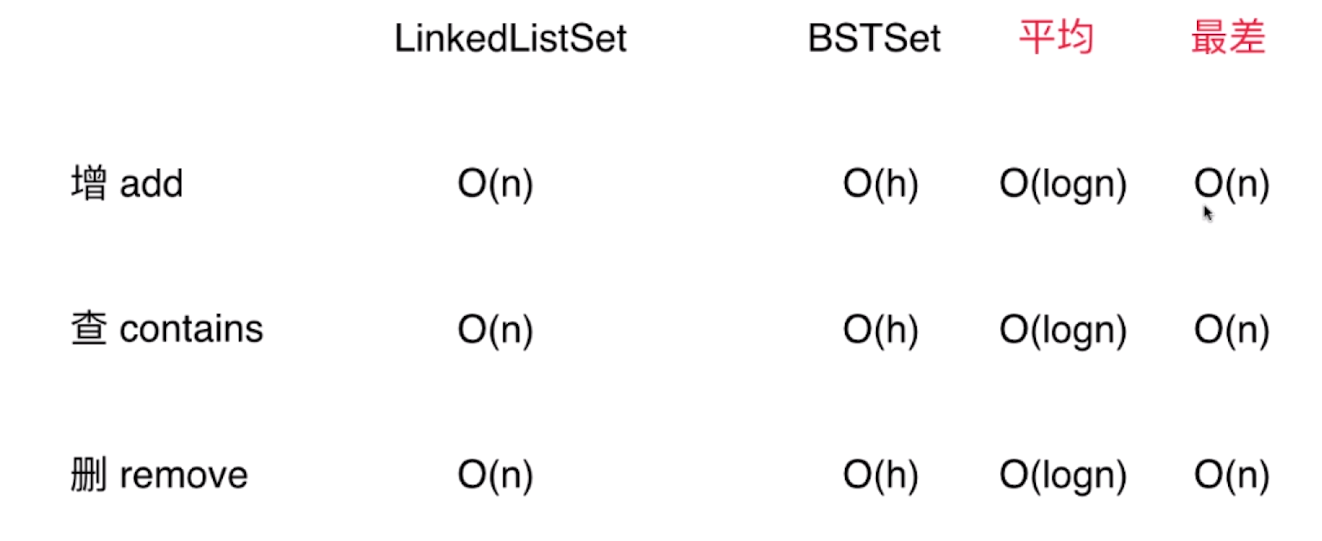
在这里插入图片描述
在这里插入图片描述

7-4 LeetCode中的集合问题

LeetCode 804

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import java.util.TreeSet;

public class Solution {

    public int uniqueMorseRepresentations(String[] words) {

        String[] codes = {".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."};
        TreeSet<String> set = new TreeSet<>();
        for(String word: words){
            StringBuilder res = new StringBuilder();
            for(int i = 0 ; i < word.length() ; i ++)
                res.append(codes[word.charAt(i) - 'a']);

            set.add(res.toString());
        }

        return set.size();
    }
}

7-5 映射基础

在这里插入图片描述
在这里插入图片描述

复制代码
1
2
3
4
5
6
7
8
9
10
11
public interface Map<K, V> {

    void add(K key, V value);
    V remove(K key);
    boolean contains(K key);
    V get(K key);
    void set(K key, V newValue);
    int getSize();
    boolean isEmpty();
}

7-6 基于链表的映射实现

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
import java.util.ArrayList;

public class LinkedListMap<K, V> implements Map<K, V> {

    private class Node{
        public K key;
        public V value;
        public Node next;

        public Node(K key, V value, Node next){
            this.key = key;
            this.value = value;
            this.next = next;
        }

        public Node(K key, V value){
            this(key, value, null);
        }

        public Node(){
            this(null, null, null);
        }

        @Override
        public String toString(){
            return key.toString() + " : " + value.toString();
        }
    }

    private Node dummyHead;
    private int size;

    public LinkedListMap(){
        dummyHead = new Node();
        size = 0;
    }

    @Override
    public int getSize(){
        return size;
    }

    @Override
    public boolean isEmpty(){
        return size == 0;
    }

    private Node getNode(K key){
        Node cur = dummyHead.next;
        while(cur != null){
            if(cur.key.equals(key))
                return cur;
            cur = cur.next;
        }
        return null;
    }

    @Override
    public boolean contains(K key){
        return getNode(key) != null;
    }

    @Override
    public V get(K key){
        Node node = getNode(key);
        return node == null ? null : node.value;
    }

    @Override
    public void add(K key, V value){
        Node node = getNode(key);
        if(node == null){
            dummyHead.next = new Node(key, value, dummyHead.next);
            size ++;
        }
        else
            node.value = value;
    }

    @Override
    public void set(K key, V newValue){
        Node node = getNode(key);
        if(node == null)
            throw new IllegalArgumentException(key + " doesn't exist!");

        node.value = newValue;
    }

    @Override
    public V remove(K key){

        Node prev = dummyHead;
        while(prev.next != null){
            if(prev.next.key.equals(key))
                break;
            prev = prev.next;
        }

        if(prev.next != null){
            Node delNode = prev.next;
            prev.next = delNode.next;
            delNode.next = null;
            size --;
            return delNode.value;
        }

        return null;
    }
}

7-7 基于二分搜索树的映射实现

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
import java.util.ArrayList;

public class BSTMap<K extends Comparable<K>, V> implements Map<K, V> {

    private class Node{
        public K key;
        public V value;
        public Node left, right;

        public Node(K key, V value){
            this.key = key;
            this.value = value;
            left = null;
            right = null;
        }
    }

    private Node root;
    private int size;

    public BSTMap(){
        root = null;
        size = 0;
    }

    @Override
    public int getSize(){
        return size;
    }

    @Override
    public boolean isEmpty(){
        return size == 0;
    }

    // 向二分搜索树中添加新的元素(key, value)
    @Override
    public void add(K key, V value){
        root = add(root, key, value);
    }

    // 向以node为根的二分搜索树中插入元素(key, value)，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, K key, V value){

        if(node == null){
            size ++;
            return new Node(key, value);
        }

        if(key.compareTo(node.key) < 0)
            node.left = add(node.left, key, value);
        else if(key.compareTo(node.key) > 0)
            node.right = add(node.right, key, value);
        else // key.compareTo(node.key) == 0
            node.value = value;

        return node;
    }

    // 返回以node为根节点的二分搜索树中，key所在的节点
    private Node getNode(Node node, K key){

        if(node == null)
            return null;

        if(key.equals(node.key))
            return node;
        else if(key.compareTo(node.key) < 0)
            return getNode(node.left, key);
        else // if(key.compareTo(node.key) > 0)
            return getNode(node.right, key);
    }

    @Override
    public boolean contains(K key){
        return getNode(root, key) != null;
    }

    @Override
    public V get(K key){

        Node node = getNode(root, key);
        return node == null ? null : node.value;
    }

    @Override
    public void set(K key, V newValue){
        Node node = getNode(root, key);
        if(node == null)
            throw new IllegalArgumentException(key + " doesn't exist!");

        node.value = newValue;
    }

    // 返回以node为根的二分搜索树的最小值所在的节点
    private Node minimum(Node node){
        if(node.left == null)
            return node;
        return minimum(node.left);
    }

    // 删除掉以node为根的二分搜索树中的最小节点
    // 返回删除节点后新的二分搜索树的根
    private Node removeMin(Node node){

        if(node.left == null){
            Node rightNode = node.right;
            node.right = null;
            size --;
            return rightNode;
        }

        node.left = removeMin(node.left);
        return node;
    }

    // 从二分搜索树中删除键为key的节点
    @Override
    public V remove(K key){

        Node node = getNode(root, key);
        if(node != null){
            root = remove(root, key);
            return node.value;
        }
        return null;
    }

    private Node remove(Node node, K key){

        if( node == null )
            return null;

        if( key.compareTo(node.key) < 0 ){
            node.left = remove(node.left , key);
            return node;
        }
        else if(key.compareTo(node.key) > 0 ){
            node.right = remove(node.right, key);
            return node;
        }
        else{   // key.compareTo(node.key) == 0

            // 待删除节点左子树为空的情况
            if(node.left == null){
                Node rightNode = node.right;
                node.right = null;
                size --;
                return rightNode;
            }

            // 待删除节点右子树为空的情况
            if(node.right == null){
                Node leftNode = node.left;
                node.left = null;
                size --;
                return leftNode;
            }

            // 待删除节点左右子树均不为空的情况

            // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
            // 用这个节点顶替待删除节点的位置
            Node successor = minimum(node.right);
            successor.right = removeMin(node.right);
            successor.left = node.left;

            node.left = node.right = null;

            return successor;
        }
    }
}

7-8 映射的复杂度分析

在这里插入图片描述

7-9 LeetCode上更多集合和映射的问题

349. 两个数组的交集

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import java.util.ArrayList;
import java.util.TreeSet;

class Solution349 {
    public int[] intersection(int[] nums1, int[] nums2) {

        TreeSet<Integer> set = new TreeSet<>();
        for(int num: nums1)
            set.add(num);

        ArrayList<Integer> list = new ArrayList<>();
        for(int num: nums2){
            if(set.contains(num)){
                list.add(num);
                set.remove(num);
            }
        }

        int[] res = new int[list.size()];
        for(int i = 0 ; i < list.size() ; i ++)
            res[i] = list.get(i);
        return res;
    }
}

350. 两个数组的交集 II

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import java.util.ArrayList;
import java.util.TreeMap;

public class Solution350 {

    public int[] intersect(int[] nums1, int[] nums2) {

        TreeMap<Integer, Integer> map = new TreeMap<>();
        for(int num: nums1){
            if(!map.containsKey(num))
                map.put(num, 1);
            else
                map.put(num, map.get(num) + 1);
        }

        ArrayList<Integer> res = new ArrayList<>();
        for(int num: nums2){
            if(map.containsKey(num)){
                res.add(num);
                map.put(num, map.get(num) - 1);
                if(map.get(num) == 0)
                    map.remove(num);
            }
        }

        int[] ret = new int[res.size()];
        for(int i = 0 ; i < res.size() ; i ++)
            ret[i] = res.get(i);

        return ret;
    }
}

最后

以上就是稳重河马最近收集整理的关于第7章 集合和映射7-1 集合基础和基于二分搜索树的集合实现7-2 基于链表的集合实现7-3 集合类的复杂度分析7-4 LeetCode中的集合问题7-5 映射基础7-6 基于链表的映射实现7-7 基于二分搜索树的映射实现7-8 映射的复杂度分析7-9 LeetCode上更多集合和映射的问题的全部内容，更多相关第7章内容请搜索靠谱客的其他文章。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(74)

相关文章

scala学习复习笔记超详细（项目-客户信息管理系统）
scala学习复习笔记超详细（项目-客户信息管理系统）
运营商大数据获客，如何针对企业营销痛点，进行精准获客
运营商大数据获客，如何针对企业营销痛点，进行精准获客
14 Scala 实现客户信息管理系统客户信息管理系统
14 Scala 实现客户信息管理系统客户信息管理系统
Scala基础和函数
Scala基础和函数
第7章 集合和映射7-1 集合基础和基于二分搜索树的集合实现7-2 基于链表的集合实现7-3 集合类的复杂度分析7-4 LeetCode中的集合问题7-5 映射基础7-6 基于链表的映射实现7-7 基于二分搜索树的映射实现7-8 映射的复杂度分析7-9 LeetCode上更多集合和映射的问题
第7章 集合和映射7-1 集合基础和基于二分搜索树的集合实现7-2 基于链表的集合实现7-3 集合类的复杂度分析7-4 LeetCode中的集合问题7-5 映射基础7-6 基于链表的映射实现7-7 基于二分搜索树的映射实现7-8 映射的复杂度分析7-9 LeetCode上更多集合和映射的问题
大数据学习(十七)scala实现actor模型管理系统
大数据学习(十七)scala实现actor模型管理系统
scala char_Scala中的Char数据类型
scala char_Scala中的Char数据类型
基于Scala设计简易的会员卡管理系统
基于Scala设计简易的会员卡管理系统

评论列表共有 0 条评论

立即
投稿
返回
顶部