取模的公式与性质

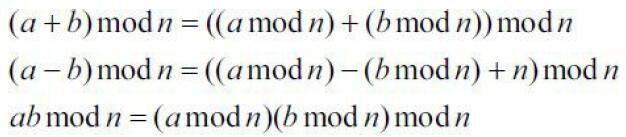
注意在减法中，由于a mod n可能小于b mod n，需要在结果加上n，而在乘法中，需要注
意a mod n和b mod n相乘是否会溢出。例如，当n=109时，ab mod n一定在int范围内，但a mod
n和b mod n的乘积可能会超过int。需要用long long保存中间结果。
如果n本身超过int但又在long long范围内，上述方法就不适用了。在这种情况下，建议使用高精度乘法

大整数取模

把大整数写成“自左向右”的形式：1234=((1*10+2)*10+3)*10+4，然后用前面的公
式，每步取模。

/*
ZhangBinjie@Penguin
*/
#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
using namespace std;
int main(){
string a;
int b, ans = 0;
while(cin >> a >> b){
ans = 0;
for(int i=0;i<a.length();++i){
ans = (int)((long long)ans * 10 + a[i] - 48)% b;
}
cout << ans << endl;
}
return 0;
}

幂取模

O(n)

/*
ZhangBinjie@Penguin
//幂取模
O(n)
*/
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int pow_mod(const int &a,const int &n,const int &m){
int ans = 1;
for(int i = 0;i < n;++i){
ans = (int)((long long)ans * a % m);
}
return ans;
}
int main(){
int a, n, m;
while(cin >> a >> n >> m){
cout<< pow_mod(a,n,m)<<endl;
}
return 0;
}

O(longn)

/*
ZhangBinjie@Penguin
//幂取模
O(longn)
//还能再用记忆化优化 吧？
*/
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int pow_mod(const int &a,const int &n,const int &m){
if(n == 0)
return 1;
int x = pow_mod (a,n/2,m);
long long ans = (long long)x * x % m;
if(n % 2 == 1)
ans = ans * a % m;
return (int)ans;
}
int main(){
int a, n, m;
while(cin >> a >> n >> m){
cout<< pow_mod(a,n,m)<<endl;
}
return 0;
}

模线性方程组

输入a, b, n 求解ax≡b(mod n)
显然 ax-b = ny (n为整数）
移项得到 ax-ny = b (n为整数）
这就变成了拓展欧几里得求直线上的点
另外：这样求的的x实际上时同余等价类，即 x≡y(mod n)
具体求解见我的上一篇文章

最后

以上就是有魅力吐司为你收集整理的同余与模算术取模的公式与性质大整数取模幂取模模线性方程组的全部内容，希望文章能够帮你解决同余与模算术取模的公式与性质大整数取模幂取模模线性方程组所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。