社区发现之模块度实现方式2

60 阅读 0 评论 40 点赞

我是靠谱客的博主动听石头，最近开发中收集的这篇文章主要介绍社区发现之模块度实现方式2，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

上次文章写了一个模块度的代码模块度，是基于公式（1）来写的。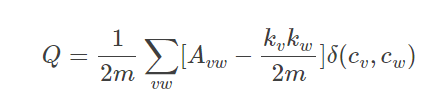
公式（1）
对于公式（2）来说，在代码实现一块这两个其实差别并不是很大。只是对于矩阵的描述不同而已。相比来说公式2更加的方便。

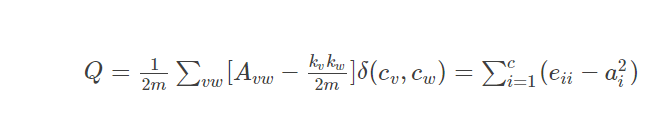
公式(2)
先放出代码：

def Q(array):
    edges = sum(sum(array))
    e =array/edges
    a =np.sum(e,axis=0)#代表与社区的连边数占总边数的比例
    q=0
    for i in range(len(e)):
        q+= e[i,i] - a[i] *a[i]
    return q
if __name__ == '__main__':
    import numpy as np
    #此为社区矩阵，节点A,B,C各自代表一个社区
    array = np.array([[0, 1, 1],
                      [1, 0, 0],
                      [1, 0, 0]])
    print(Q(array))
    #此为社区矩阵节点A,B为一个社区，节点C单独为一个社区
    array2 =np.array([[2,1],
                      [1,0]])
    print(Q(array2))

在我第一个实现模块度的代码（对应公式（1））里，array代表着图矩阵，cluster代表社区的划分，比如cluster= [2, 1, 2]，分别对那个[A,B,C]三个节点，其中AC的label相同且为2所以AC节点为一个社区。
在本文代码里array和array1代表社区矩阵，其实就是将label和矩阵合二为一了，其中代码中的array描述了图1ABC三个节点各自为一个社区array[0,0]可以理解为A节点所代表的社区的边数，a[0,1]代表AB节点的边数。
array2代表着社区矩阵，其中AB为一个社区,C为一个社区。
如不理解可以私信我。