循环队列的数组实现（）

60 阅读 0 评论 40 点赞

我是靠谱客的博主含蓄小懒虫，最近开发中收集的这篇文章主要介绍循环队列的数组实现（），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

理论知识

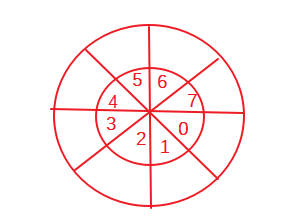
由于顺序存储的队列会产生“假溢出的情况”，我们可以将队列的存储结构臆想为一个闭合的环状结构，这便是我们所说的循环队列，如下图所示。
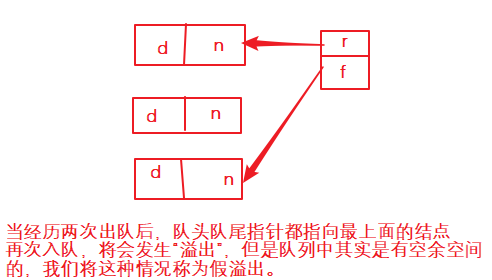假溢出图示循环队列的逻辑结构
在这里插入图片描述但是循环队列中，判断队空和堆满的条件都是Q.rear = Q.front,这给我们的编程实现带来了很多麻烦，这样我们会有三种处理方法，
1.牺牲一个存储单元，入队的时候将队头指针在队尾指针的下一位置最为队列满的条件
这是判断队空的条件仍然是：Q.rear = Q.front
但是判断队满的条件变为：(Q.rear+1)%MAXSIZE = Q.front
队列中元素的个数为:(Q.rear-Q.front+MAXSIZE)%MAXSIZE
2.在结构体的定义中增加表示元素个数的成员
队空：Q.size = 0
队满：Q.size = MAXSIZE
队列元素个数：Q.size
3.第一种情况牺牲的存储空间利用起来，当flag = 0时，因为删除发生了Q.rear = Q.front 则表示队空，当flag = 1时，因为增加导致了Q.rear = Q.front 则表示队满

以下使用第一种方法进行代码实现

存储结构

typedef struct {
	int data[MAXSIZE];
	int front,rear;
}Quene;

初始化

//初始化
void initQuene(Quene &Q){
	Q.rear = Q.front = 0;
}

判空

bool isEmpty(Quene &Q){
	if((Q.rear+1)%MAXSIZE == Q.front){
		cout<<"队列已满"<<endl;
		return true;
	}
	return false;
}

入队

//入队
bool push(Quene &Q,int e){
	if(!isEmpty(Q)){
		Q.data[Q.rear] = e;
		Q.rear = (Q.rear+1) % MAXSIZE;
		return true; 
	}
	return false;
}

出队

//出队
bool pop(Quene &Q){
	if(Q.rear == Q.front){
		return false;
	}else{
		Q.data[Q.front] = -1;
		Q.front = (Q.front+1)%MAXSIZE;
		return true;
	}
}

整合测试

#include<iostream>
using namespace std;
#define MAXSIZE 4
typedef struct {
	int data[MAXSIZE];
	int front,rear;
}Quene;
//初始化
void initQuene(Quene &Q){
	Q.rear = Q.front = 0;
}
//判空 
bool isEmpty(Quene &Q){
	if((Q.rear+1)%MAXSIZE == Q.front){
		cout<<"队列已满"<<endl;
		return true;
	}
	return false;
}
//入队
bool push(Quene &Q,int e){
	if(!isEmpty(Q)){
		Q.data[Q.rear] = e;
		Q.rear = (Q.rear+1) % MAXSIZE;
		return true; 
	}
	return false;
}
//出队
bool pop(Quene &Q){
	if(Q.rear == Q.front){
		return false;
	}else{
		Q.data[Q.front] = -1;
		Q.front = (Q.front+1)%MAXSIZE;
		return true;
	}
}
int main()
{
	Quene Q;
	initQuene(Q);
	push(Q,1);
	cout << Q.data[Q.rear-1] << endl;
	push(Q,2);
	cout << Q.data[Q.rear-1] << endl;
	push(Q,3);
	cout << Q.data[Q.rear-1] << endl;
	push(Q,4);
	cout << Q.data[Q.front] << endl;
	pop(Q);
	cout << Q.data[Q.front] << endl;
	pop(Q);
	cout << Q.data[Q.front] << endl;
	return 0;
 }