队Queue也是一个线性的存储结构，原则是先入先出（FIFO），区别于栈的先进后出。就类似与排队买票，先进入队列的就先买票出列；入队在一端操作（队尾），出队只能在另一端操作（队首）；
一个队列的基本操作就是入队，出队，获取队列大小，判断是否为空等等；这篇博客就是自己实现一个基于数组的队列和循环队列。
根据上面的分析，创建一个Queue接口，提供入队，出队，判空等操作：
复制代码
1
2
3
4
5
6
7public interface Queue<E> { //使用泛型使得队列可以存储各种类型的元素 void enqueue(E e); //入队（从队尾操作） E dequeue(); //出队，返回出队的元素（从队首操作） public int getSize(); //获取队列中元素的个数 boolean isEmpty(); //判断队列是否为空 E front(); //获取队首的元素 }
下面，基于数组实现一个队列，来看看具体的方法怎么实现：
为了实现队列的可扩容，我们用于实现的数组是博客“数据结构（一）——封装动态数组”中的动态数组；具体的原理可以查看之前的那篇博客，这里只贴代码：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170package com.itheima.array; /** * @author GuoBaoYu * 使用泛型，可以存放任意类型的数据； */ public class Array<E> { private E[] data; //内部是静态数组 private int size; public Array(int capacity) { data =(E[]) new Object[capacity]; size = 0; } /** * 默认构造一个容量为10的数组 */ public Array() { this(10); } public int getCapacity(){ return data.length; } public boolean isEmpty(){ return size==0 ; } public int getSize(){ return size; } public void addLast(E element){ add(size, element); } public void addFirst(E element){ add(0,element); } //动态数组进行自动扩容和减少容量 private void resize(int newCapacity){ E[] newData = (E[]) new Object[newCapacity]; for(int i = 0; i < size;i++){ newData[i] = data[i]; } data = newData; } /** * @param index * @param element * 向指定的位置插入元素 */ public void add(int index,E element){ if(size == getCapacity()){ // throw new IllegalArgumentException("AddLast is failed. Array is full."); // 之前如果数组空间满了，抛出异常；现在进行扩容 int newCapacity = getCapacity()*2; resize(newCapacity); } if(index < 0 || index > size){ throw new IllegalArgumentException("Argument index is illegal.index is required index >=0 and index <= size. "); } for(int i = size-1; i>=index; i--){ data[i+1] = data[i]; } data[index] = element; size++; } @Override public String toString(){ StringBuilder builder = new StringBuilder(); builder.append(String.format("size = %d,capacity = %dt", size,getCapacity())); builder.append("["); for(int i = 0; i < size; i++){ builder.append(data[i]); if(i<size-1){ builder.append(","); } } builder.append("]"); return builder.toString(); } public E get(int index){ if(index >=size || index <0){ throw new IllegalArgumentException("Argument index is illegal."); } return data[index]; } public void set(int index, E element){ if(index >=size || index <0){ throw new IllegalArgumentException("Argument index is illegal."); } data[index] = element; } public boolean contains(E element){ for(int i =0; i <size;i++){ if(data[i].equals(element)){ return true; } } return false; } public E getFirst(){ return get(0); } public E getLast(){ return get(size-1); } public int find(E element){ for(int i=0 ; i < size; i++){ if(data[i].equals(element)){ return i; } } return -1; } //删除index位置的元素，并返回删除的元素的值 public E remove(int index){ if(index < 0 || index >= size){ throw new IllegalArgumentException("Remove failed.index is an illegal argument."); } E element = data[index]; for(int i = index+1; i < size; i++){ data[i-1] = data[i]; } size--; if(size <= getCapacity() /4 && data.length/2 !=0){ resize(getCapacity()/2); } return element; } //删除第一个元素 public E removeFirst(){ return remove(0); } //删除最后一个元素 public E removeLast(){ return remove(size-1); } /** * @param element * @return * 删除指定的数据 */ public boolean removeElement(E element){ int find = find(element); if(find!=-1){ remove(find); return true; } return false; } }
基于这个动态数组Array，实现一个队列：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61package com.itheima.queue; import com.itheima.array.Array; public class ArrayQueue<E> implements Queue<E>{ private Array<E> array; public ArrayQueue() { array = new Array<E>(10); } //允许用户指定队列的容量 public ArrayQueue(int capacity){ array = new Array<E>(capacity); } public int getCapacity(){ return array.getCapacity(); } //入队从数组的尾部操作 public void enqueue(E e) { array.addLast(e); //入队时队列是否满，是否触发扩容操作在array.addLast()方法中考虑，所以这里直接调用； } //出队从数组的首部操作 public E dequeue() { return array.removeFirst(); //出队时队列是否为空，是否触发缩容操作在array.removeFirst()方法中考虑，所以这里直接调用； } public int getSize() { return array.getSize(); } public boolean isEmpty() { return array.isEmpty(); } public E getFront() { return array.getFirst(); } @Override public String toString() { StringBuilder res = new StringBuilder(); res.append("ArrayQueue:"); res.append("front:["); for(int i = 0; i < array.getSize();i++){ res.append(array.get(i)); if(i < array.getSize()-1){ res.append(","); } } res.append("] tail"); return res.toString(); } }
一个简单的测试：
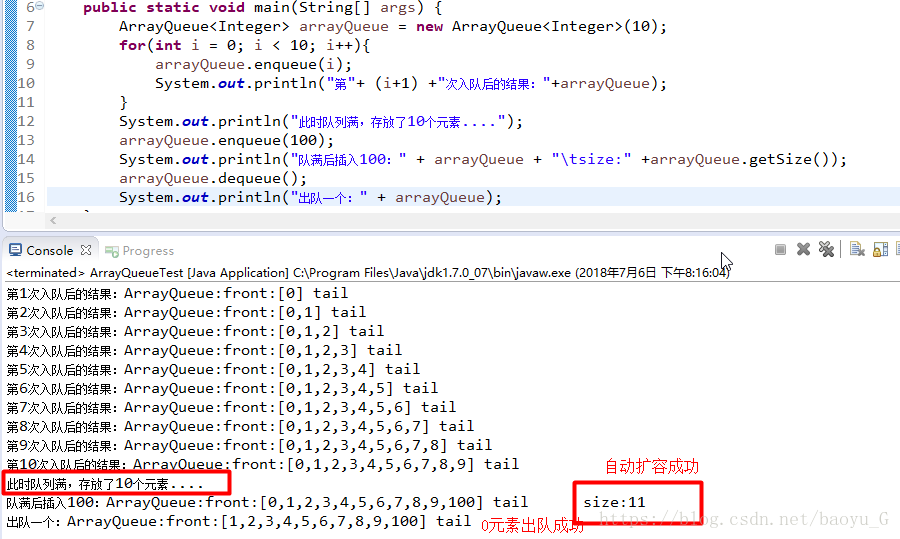
上面的这种实现方式可以实现队列的动态扩容。但是依旧存在一定的缺陷：基于数组实现的队列，在进行出队操作时是调用了数组的removeFirst()方法，移除数组下标为0的元素，后面的每个元素向前移动一个位置，再进行size--,时间复杂度为o(n):过程如下：(第三步的size还要进行size--，标在4的位置，图截错了..这里声明一下)
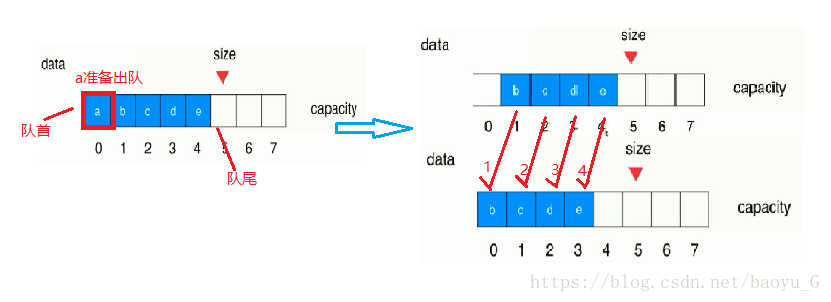
为了解决这一点，在数组队列的基础上改进循环队列：基本思路是，在进行入队和出队操作(主要为了出队操作，不需要移动数组中元素的位置)，只需要维护队列（数组）的front（头）和tail（尾）的值，出队变成了O（1）的操作；
使用这种方式的另一个好处是构成了循环队列：什么是循环呢？
当出现下面这种存储情况时：
看起来不能再入队，tail不能再进行tail++了，因为tail指示的是队尾的后面第一个空的位置；但是实际上并不是不能再入队，而是可以把数组看成一个环，数组的前面还有空间，tail变为(tail+1)%8=0,tail指示在下标为0的空间！所以tail真正的操作应该是（tail+1）%数组长度；
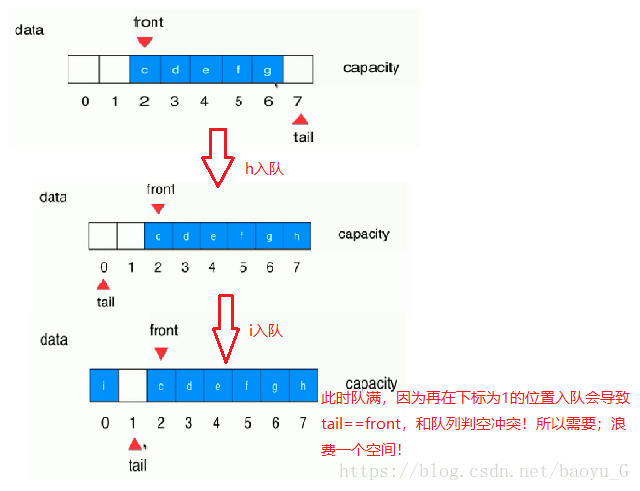
以上就是循环队列的基本思想。下面是循环队列的实现，是基于普通静态数组的：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108package com.itheima.queue; import com.itheima.array.Array; /** * @author GuoBaoYu * * @param <E> * 循环队列 */ public class LoopQueue<E> implements Queue<E> { private E[] data; private int front,tail; private int size; //队列的元素的个数 public LoopQueue(int capacity) { //用户想要存放capacity个数据，根据之前的原理分析，为了防止判空和判满冲突，需要预留一个空间！ data = (E[]) new Object[capacity+1]; front = 0; tail = 0; size = 0; } public LoopQueue() { this(10); } public int getCapacity(){ return data.length-1; } /* (non-Javadoc) * @see com.itheima.queue.Queue#enqueue(java.lang.Object) * 入队： * 1.如果队满，调用resize()方法进行扩容； * 2.把数据放入tail的位置 * 3.维护tail和size的值 */ public void enqueue(E e) { if( (tail+1)% data.length == front){ //数组判满；进行%data.length是为了让数组循环起来 //TODO 队列满了以后进行扩容 resize(getCapacity() *2); } data[tail] = e; tail = (tail+1)%data.length; size++; } private void resize(int newCapacity) { E[] newData = (E[]) new Object[newCapacity + 1]; for(int i= 0; i < size;i++){ newData[i] = data[(front+i)% data.length]; } data = newData; front = 0; tail = size; } public E dequeue() { if(isEmpty()){ throw new IllegalArgumentException("Cannot dequeue from an empty queue."); } E ret = data[front]; data[front] = null; front = (front+1)%data.length; size--; if(size==getCapacity()/4 && getCapacity()/2!=0){ resize(getCapacity()/2); } return ret; } public int getSize() { return size; } public boolean isEmpty() { return front == tail; } public E front() { if(isEmpty()){ throw new IllegalArgumentException("No elements in this queue."); } return data[front]; } @Override public String toString() { StringBuilder res = new StringBuilder(); res.append("LoopQueue:"); res.append("front:["); for(int i = front; i != tail;i = (i+1)%data.length){ res.append(data[i]); if((i +1)% data.length != tail){ res.append(","); } } res.append("] tail"); return res.toString(); } }
一个简单的测试：
可以看到，出队的结果和使用removeFirst()达到的效果是一样的；
代码中值得注意的地方在于自动调整容量的resize()方法的实现和遍历队列的toString()方法：
在进行入队时，先根据之前分析的条件，(tail+1)%data.length==front判断是否队满，如果队满进行扩容。扩容的思路是将队列数组的大小调整为原来的2倍，当然也可以是1.5倍，看个人了；当需要扩容时，数组中的元素可能是这样存放的：
要想调整为容量为16的数组，我们完全没有必要还按这个顺序存放数据，可以像下面这样：
相当于在扩容的同时对数据进行了整理；还是创建一个两倍大小+1的数组，新数组的0位置对应原来的front，1对应front+1......
位置都存在front的偏移，所以有了resize()代码中：把data[(front+i)%data.length]赋值给newData[i]
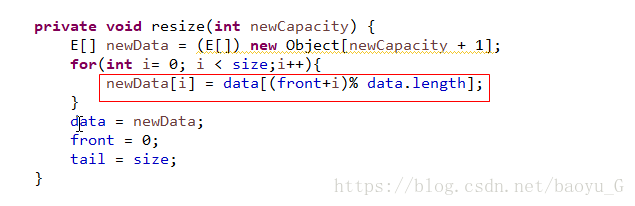
最后更改data的指向，维护新数组的front和tail的值；如此实现扩容！当然resize()方法只是传递了一个新的容量作为参数；在enqueue()方法中传递一个大的新容量作为扩容；当出队很多数据后可以传递一个小的容量，进行缩容。
在覆盖toString()方法时，和之前的从下标为0开始遍历不同，变为从front开始遍历，直到遍历到最后一个元素，也需要注意一下。
以上就是一个循环队列的实现，把出队操作的时间复杂度降为了O（1）。
下面通过测试比较一下两种队列的效率：
可以看到对10000个数据的出队，LoopQueue循环队列的效率远高于ArrayQueue；
最后
以上就是聪明小伙最近收集整理的关于数据结构（三）——基于数组的队列和循环队列的全部内容，更多相关数据结构（三）——基于数组内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复