Swin Transformer

论文地址:https://arxiv.org/abs/2103.14030

代码地址:https://github.com/microsoft/Swin-Transformer

https://www.bilibili.com/video/BV13L4y1475U 感谢沐神,朱毅，感谢霹雳大佬！！！！

1. 简介

1.1 简介

Swin Transformer是2021年微软研究院发表在ICCV上的一篇文章，并且已经获得ICCV 2021 best paper的荣誉称号。Swin Transformer网络是Transformer模型在视觉领域的又一次碰撞。该论文一经发表就已在多项视觉任务中霸榜。该论文是在2021年3月发表的，现在是2021年11月了，根据官方提供的信息可以看到，现在还在COCO数据集的目标检测以及实例分割任务中是第一名。

1.2 存在的问题

个人理解

VIT使用Transformer做了图像分类。同时也留下了悬念，怎么样才能使得Transformer应用到 视觉领域的下游任务(分割，检测)中。Swin Transformer就来了

Swin Transformer 希望VIT也能像卷积神经网络一样，也能分成几个block,也能做这种层级式的特征提取。使得提取出来的特征呢，有多尺度的概念

Transformer所使用的自注意力的操作非常的耗时。

• 前人的工作呢，使用后续的特征图作为Transformer的输入
• 把图片打成patch,减少图片的resolution
• 把图片画成一个一个的小窗口，在窗口里面去做自注意力

2. 网络结构(创新点)

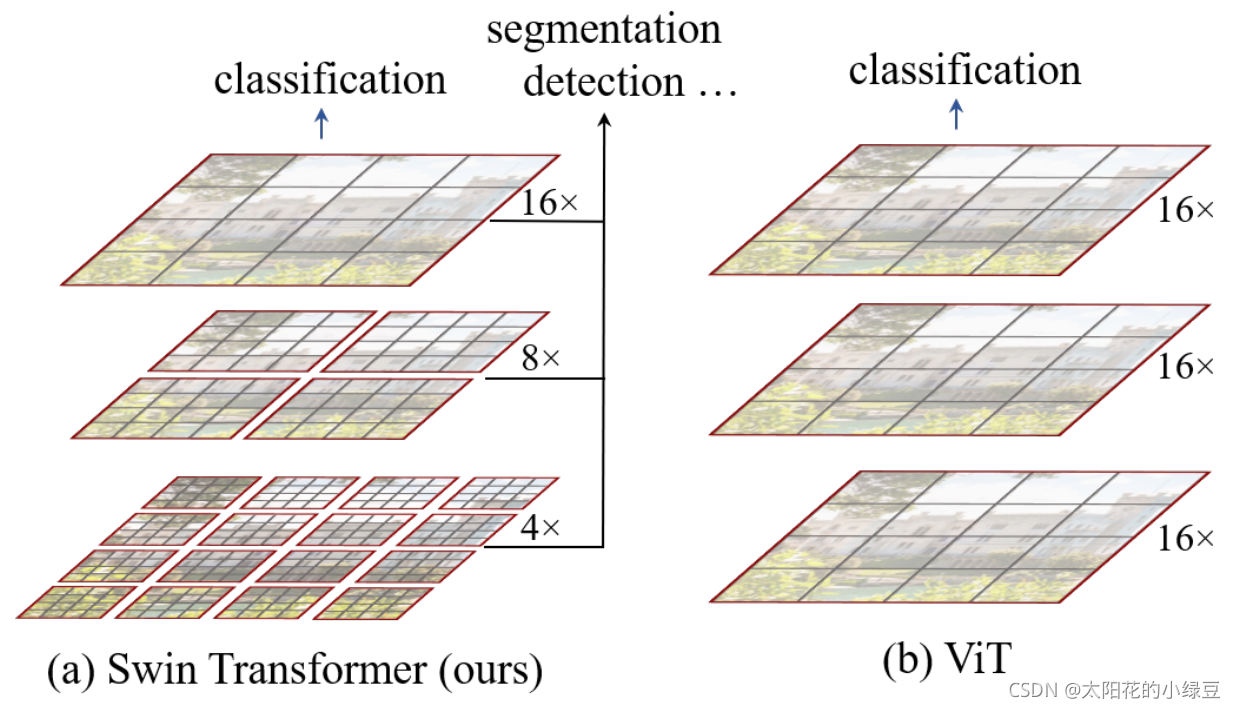
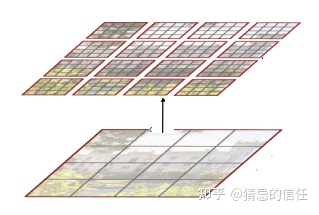
• Swin Transformer使用了类似卷积神经网络中的层次化构建方法（Hierarchical feature maps），比如特征图尺寸中有对图像下采样4倍的，8倍的以及16倍的，这样的backbone有助于在此基础上构建目标检测，实例分割等任务。而在之前的Vision Transformer中是一开始就直接下采样16倍，后面的特征图也是维持这个下采样率不变。
• 在Swin Transformer中使用了Windows Multi-Head Self-Attention(W-MSA)的概念，比如在下图的4倍下采样和8倍下采样中，将特征图划分成了多个不相交的区域（Window），并且Multi-Head Self-Attention只在每个窗口（Window）内进行。相对于Vision Transformer中直接对整个（Global）特征图进行Multi-Head Self-Attention，这样做的目的是能够减少计算量的，尤其是在浅层特征图很大的时候。这样做虽然减少了计算量但也会隔绝不同窗口之间的信息传递，所以在论文中作者又提出了 Shifted Windows Multi-Head Self-Attention(SW-MSA)的概念，通过此方法能够让信息在相邻的窗口中进行传递，后面会细讲。

下图是Swin Transformer文章中给出的图1，左边是本文要讲的Swin Transformer，右边边是之前讲的Vision Transformer。

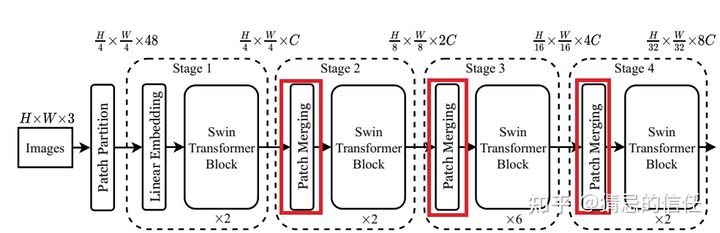
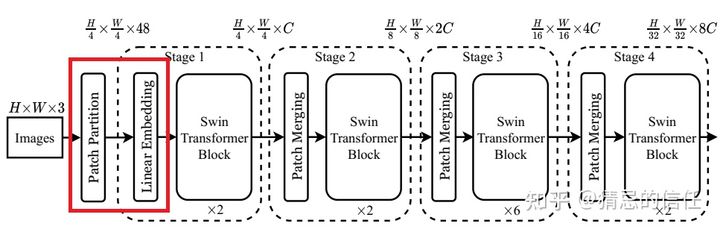
接下来，简单看下原论文中给出的关于Swin Transformer（Swin-T）网络的架构图。通过图(a)可以看出整个框架的基本流程如下：

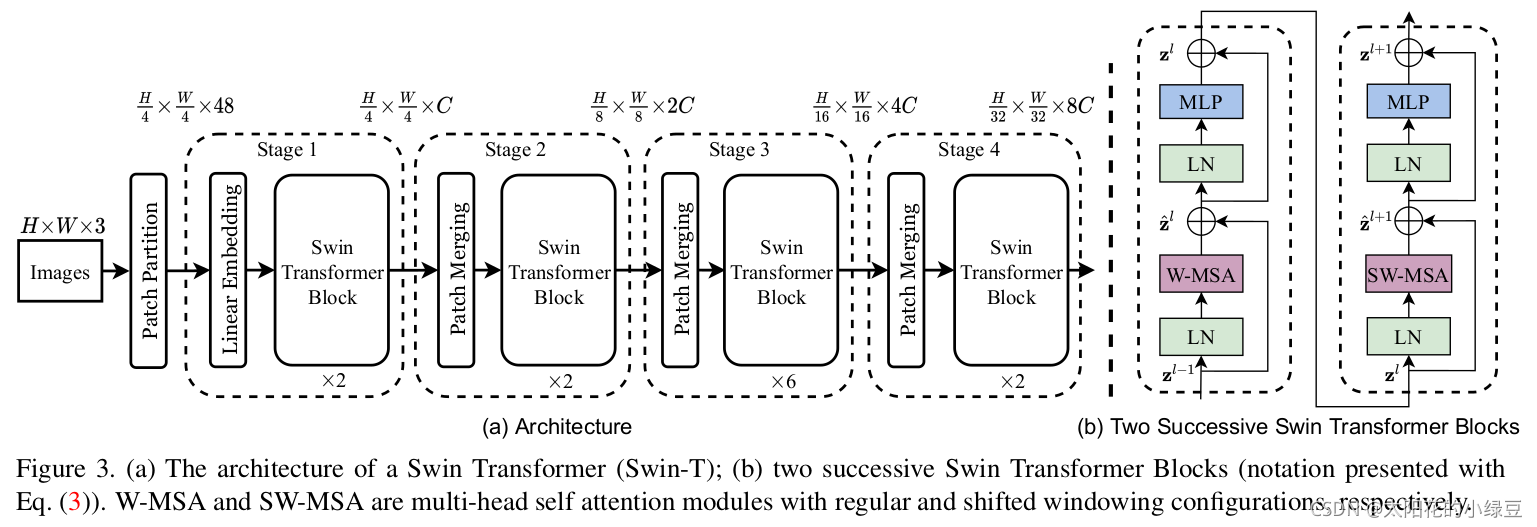
• 首先将图片输入到Patch Partition模块中进行分块，即每4x4相邻的像素为一个Patch，然后在channel方向展平（flatten）。假设输入的是RGB三通道图片，那么每个patch就有4x4=16个像素，然后每个像素有R、G、B三个值所以展平后是16x3=48，所以通过Patch Partition后图像shape由 [H, W, 3]变成了 [H/4, W/4, 48]。然后在通过Linear Embeding层对每个像素的channel数据做线性变换，由48变成C，即图像shape再由 [H/4, W/4, 48]变成了 [H/4, W/4, C]。其实在源码中Patch Partition和Linear Embeding就是直接通过一个卷积层实现的，和之前Vision Transformer中讲的 Embedding层结构一模一样。
• 然后就是通过四个Stage构建不同大小的特征图，除了Stage1中先通过一个Linear Embeding层外，剩下三个stage都是先通过一个Patch Merging层进行下采样（后面会细讲）。然后都是重复堆叠Swin Transformer Block注意这里的Block其实有两种结构，如图(b)中所示，这两种结构的不同之处仅在于一个使用了W-MSA结构，一个使用了SW-MSA结构。而且这两个结构是成对使用的，先使用一个W-MSA结构再使用一个SW-MSA结构。所以你会发现堆叠Swin Transformer Block的次数都是偶数（因为成对使用）。
• 最后对于分类网络，后面还会接上一个Layer Norm层、全局池化层以及全连接层得到最终输出。图中没有画，但源码中是这样做的。

2.1 PatchEmbedding

patchembedding 这个部分就是patch partition和 linear embedding 进行了融合

1) Patch Partition

Pacth Partition的作用就是将输入的Images转化为patch块，且每个patch块是由相邻四个像素块组成。

其本质就是将$H\times W\times 3$的Image转化为$\frac{H}{4}\times \frac{W}{4}\times 48$的patch。

可能有同学要问了48是什么？

这里跟大家解释一下，48是因为原图像的channels是3，而在图像转换为patch的时候四个相邻像素在channel方向上展平，所以$4\times 4\times 3=48$。

2) Linear Embedding

这一步没什么好说的，就是将$[\frac{H}{4}\times \frac{W}{4}\times 48]-->[\frac{H}{4}\times \frac{W}{4}\times C]$,

如果使用$Swin-T$模型，$C$的大小为96

注意点：

代码中Patch Embedding的输出是$(B,H\times W,C)$，并不是直接的$(B,H,W,C)$。

需要做归一化后，才能变成$(B,H,W,C)$这样子的格式。

2.2 Patch Merging

为了让图像有层级式的概念，就需要类似池化的操作，在Swin-Transformer中就是 patch Merging的操作

Patch Merging的作用就是将图像的高和宽缩小至原来的$\frac{1}{2}$,将$C$升为原来的2倍
$$[B,C,H,W]-->[B,2C,\frac{H}{2},\frac{W}{2}]$$

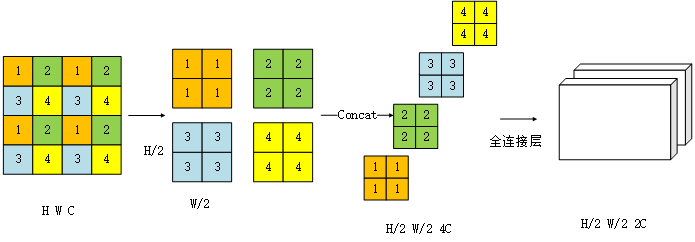
• 第一步，隔一个点选取一个数值。然后这样子宽和高就变成原来的$1/2$
• 第二步，把分开的patch ，进行通道上的融合，这样子就变成了$\frac{H}{2}\times \frac{W}{2}\times 4C$
• 第三步，为了和卷积操作一样，通道数是原来的$2$倍.又做了一个全连接操作。把通道数变成原来的$\frac{1}{2}$。把$4C$变成了$2C$

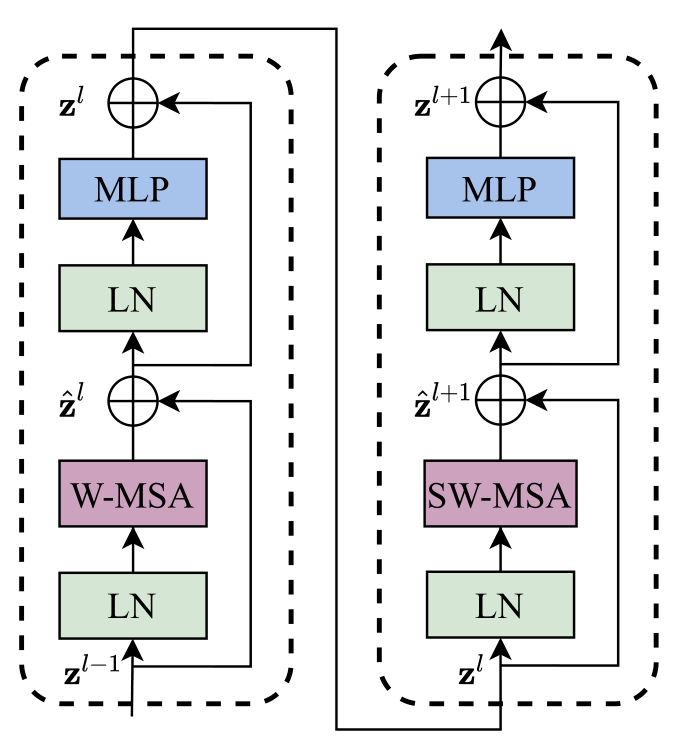
2.3 Swin Transformer

Swin Transformer的核心部分就是这个block，如图(b)所示，该block有两种。一种是具有W-MSA的block，另一种是具有SW-MSA的block。

2.3.1 W-MSA

W-MSA是一个具有节省计算量的自注意力机制，它将图像以7x7大小分割成多个窗口进行自注意力机制。传统的Multi-head Self-Attention(多头自注意力机制)具有非常大的计算量，而W-MSA的出现，很好的解决了MSA计算量庞大的问题。下面介绍一下W-MSA如何解决MSA计算庞大的问题

这两个计算公式，分别阐述了VIT的自注意力的计算复杂度计算公式，和Swin-Transformer自注意力计算复杂度的计算公式
$$\begin{gathered} \Omega (MSA)=4hw{C}^2+2(hw{)}^{2}C \\ \Omega (W-MSA)=4hw{C}^2+2M^{2}hwC \end{gathered}$$
1. 首先介绍一下参数概念

• h代表feature map的高度
• w代表feature map的宽度
• C代表feature map的深度
• M代表每个窗口（Windows）的大小

2. 介绍一下VIT的自注意力计算公式

Self-Attention的公式
$$Attention(Q,K,V)=SoftMax(\frac{Q{K}^T}{\sqrt{d}})V$$
如图所示

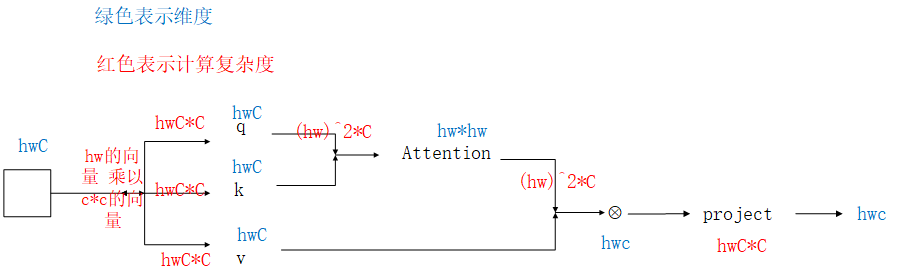
VIT的复杂度图中有展示
$$\Omega (MSA)=3hw{C}^2+(hw{)}^{2}C+(hw{)}^{2}C+hw{C}^2=4hw{C}^2+2(hw{)}^{2}C$$

3. 如果使用了窗口注意力机制

我们可以套用上面公式，在窗口里面做注意力$M\times M$。现在h->M,w->M。序列长度只有$M\times M$.

一个窗口的注意力机制如下所示
$$\Omega (One-W-MSA)=4M^2{C}^2+2M^{4}C$$
一共有$(\frac{h}{M},\frac{w}{M})$这么多个窗口
$$\Omega (W-MSA)=(\frac{h}{M}\times \frac{w}{M})(4M^2{C}^2+2M^{4}C)=4hw{C}^2+2M^{2}hwC$$

2.3.2 SW-MSA

（Shifted Windows Multi-head Self-Attention）

虽然$W-MSA$使用分割窗口操作将计算量降到了$4hw{C}^2+2M^{2}hwC$，但是带来了一个问题。那就是窗口与窗口之间的信息是闭塞的，不交互的。这样会使得图像的上下文连接不起来，从而导致模型效果差。

所以作者希望不只在一个窗口内做自注意力，而是全局的，所以需要移动窗口。

第一次是正常的窗口自注意力，第二次是移动窗口自注意力，两次是绑定的，这也是在四个阶段swin transformer都为偶数的原因

根据之前介绍的W-MSA和SW-MSA是成对使用的

• 第$L$层，对应的是左侧，是W-MSA。有4个窗口。每个窗口中有$M\times M,M=2$个元素
• 第$L+1$层，右侧就是SW-MSA。根据左右两幅图对比能够发现窗口（Windows）发生了偏移（可以理解成窗口从左上角分别向右侧和下方各偏移了$\frac{M}{2}$个像素）

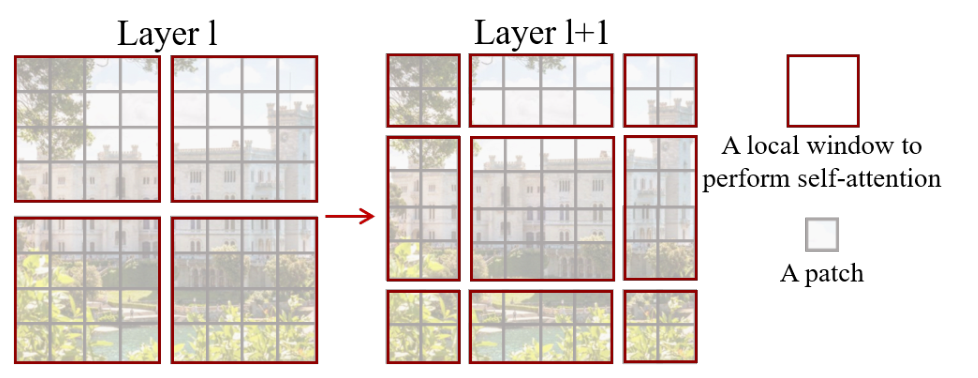
窗口之间如何进行通信呢？？

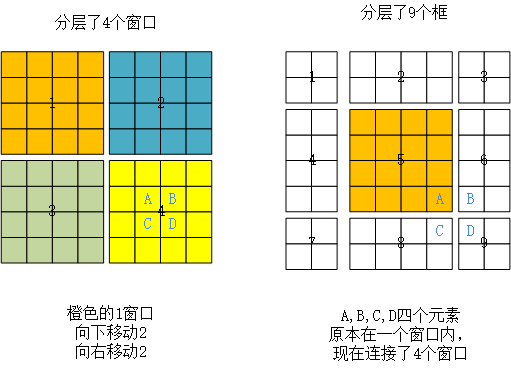
比如对于第一行第2列的2x4的窗口，它能够使第L层的第一排的两个窗口信息进行交流。再比如，第二行第二列的4x4的窗口，他能够使第L层的四个窗口信息进行交流，其他的同理。那么这就解决了不同窗口之间无法进行信息交流的问题。

根据上图，可以发现通过将窗口进行偏移后，由原来的4个窗口变成9个窗口了。后面又要对每个窗口内部进行MSA，这样做感觉又变麻烦了。为了解决这个麻烦，作者又提出而了Efficient batch computation for shifted configuration，一种更加高效的计算方法。下面是原论文给的示意图。

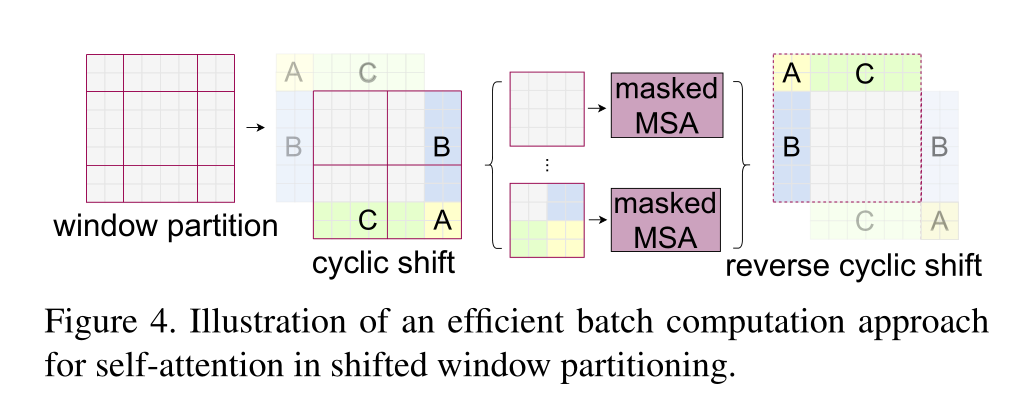
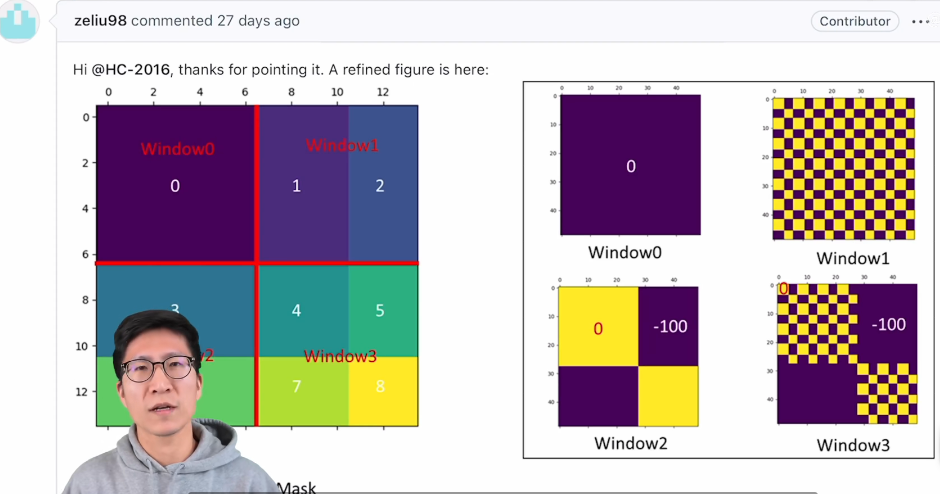
这个图比较难懂。说白了其实就是一个七巧板。下图左侧是刚刚通过偏移窗口后得到的新窗口，右侧是为了方便大家理解，对每个窗口加上了一个标识。然后0对应的窗口标记为区域A，3和6对应的窗口标记为区域B，1和2对应的窗口标记为区域C。

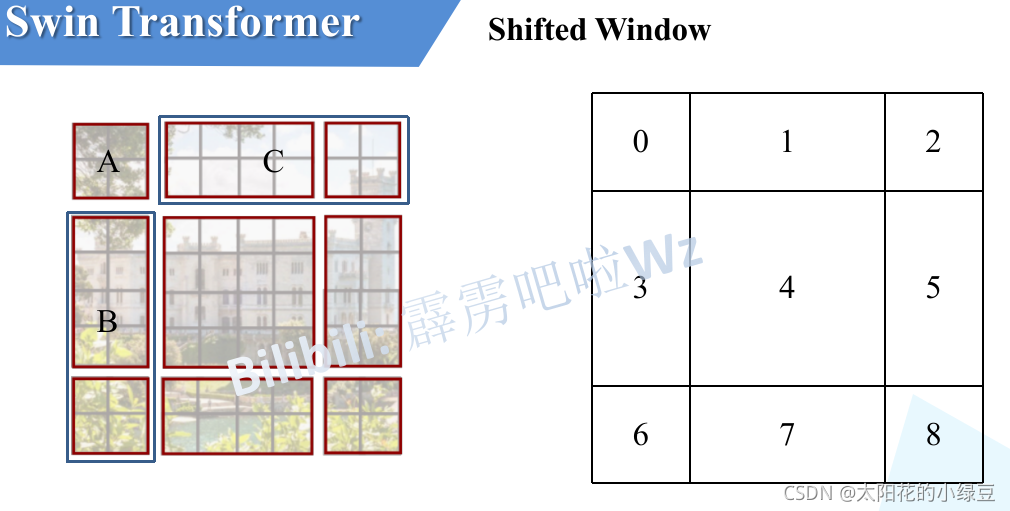
然后先将区域A和C移到最下方。

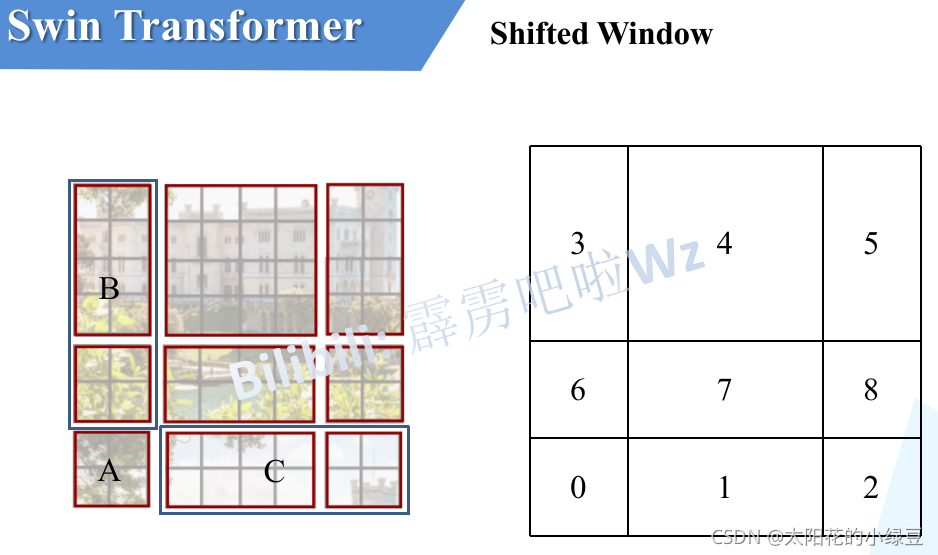
接着，再将区域A和B移至最右侧。

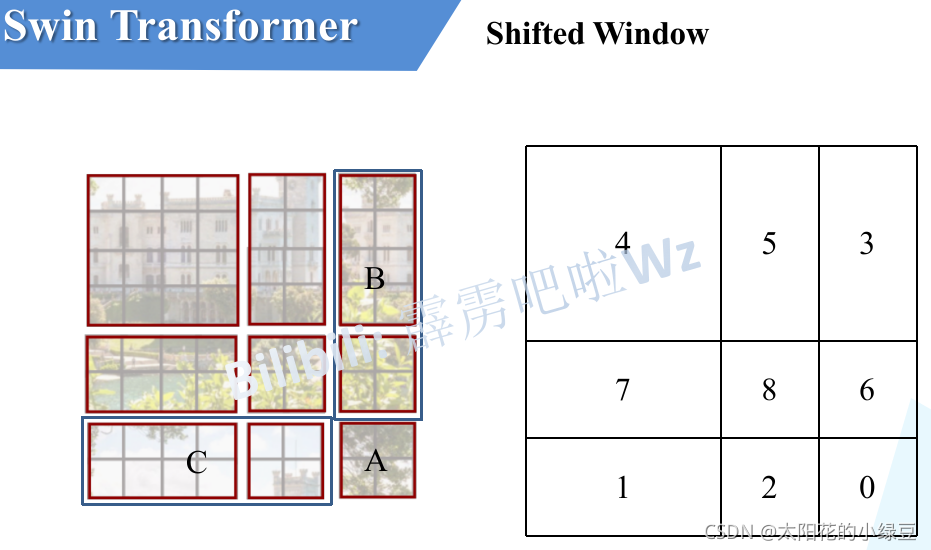
移动完后，4是一个单独的窗口；将5和3合并成一个窗口；7和1合并成一个窗口；8、6、2和0合并成一个窗口。这样又和原来一样是4个4x4的窗口了，所以能够保证计算量是一样的。这里肯定有人会想，把不同的区域合并在一起（比如5和3）进行MSA，这信息不就乱窜了吗？是的，为了防止这个问题，在实际计算中使用的是masked MSA即带蒙板mask的MSA，这样就能够通过设置蒙板来隔绝不同区域的信息了。关于mask如何使用，可以看下下面这幅图，下图是以上面的区域5和区域3为例。

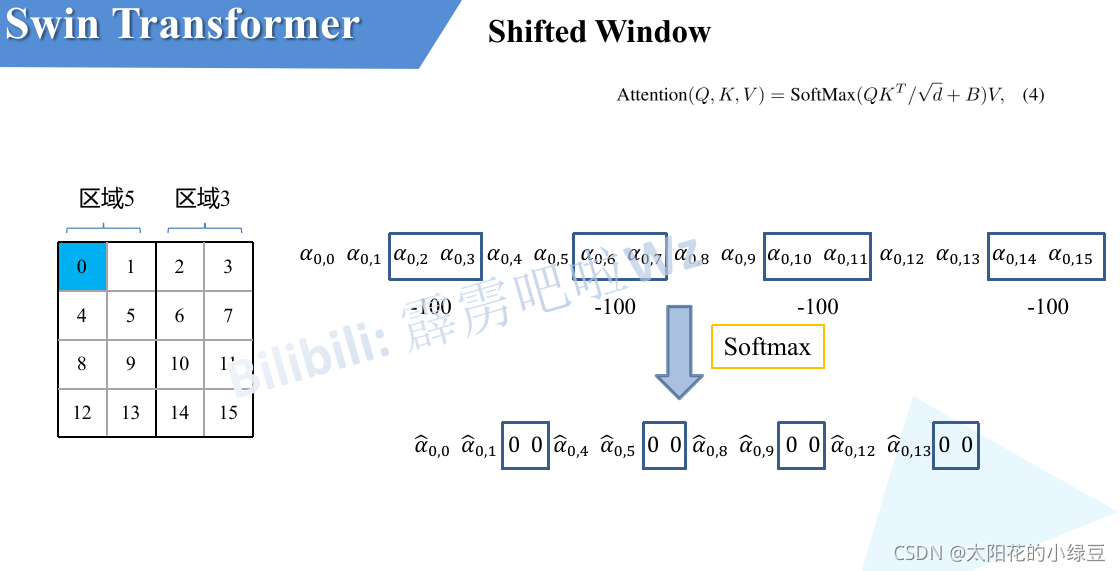
对于该窗口内的每一个像素（或称token，patch）在进行MSA计算时，都要先生成对应的query(q)，key(k)，value(v)。

假设对于上图的像素0而言,得到$q^0$后要与每一个像素的k进行匹配（match）,假设${\alpha }_{0,0}$代表与像素$0$对应的$k^0$进行匹配的结果，那么同理可以得到${\alpha }_{0,0}$至${\alpha }_{0,15}$。

按照普通的MSA计算，接下来就是SoftMax操作了。但对于这里的masked MSA,像素$0$是属于区域5的，我们只想让它和区域5内像素进行匹配。

那么我们可以将像素$0$与区域$3$的所有像素匹配结果都减去100(例如${\alpha }_{0,2},{\alpha }_{0,3},{\alpha }_{0,6},{\alpha }_{0,7}$),由于$\alpha$的值都很小，一般都是零点几的数，将其中一些数减去100后在通过SoftMax得到对应的权重都等于0了。所以对于像素0而言实际上还是只和区域5内的像素进行了MSA。

模型总体的mask操作

2.4 相对位置编码

https://mapengsen.blog.csdn.net/article/details/118696021

3. 实验

4. 代码

导入包

import torch
import torch.nn as nn
import torch.utils.checkpoint as checkpoint
from timm.models.layers import DropPath, to_2tuple, trunc_normal_

timm是pytorch常见的工具包

pip install timm

4.1 MLP

MLP部分没什么好说的，中规中矩的两个全连接层，一个激活函数。

class Mlp(nn.Module):
    def __init__(self, in_features, hidden_features=None, out_features=None, act_layer=nn.GELU, drop=0.):
        super().__init__()
        out_features = out_features or in_features
        hidden_features = hidden_features or in_features
        self.fc1 = nn.Linear(in_features, hidden_features)
        self.act = act_layer()
        self.fc2 = nn.Linear(hidden_features, out_features)
        self.drop = nn.Dropout(drop)

    def forward(self, x):
        x = self.fc1(x)
        x = self.act(x)
        x = self.drop(x)
        x = self.fc2(x)
        x = self.drop(x)
        return x

4.2 window_partition

这部分的代码就是把图像转为多个窗口，和把多个窗口还原成图像的操作，主要是为了方便W-MSA和SW-MSA的操作。

def window_partition(x, window_size):
    """
    Args:
        x: (B, H, W, C)
        window_size (int): window size
    Returns:
        windows: (num_windows*B, window_size, window_size, C)
    """
    B, H, W, C = x.shape
    x = x.view(B, H // window_size, window_size, W // window_size, window_size, C)
    windows = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(-1, window_size, window_size, C)
    return windows

第一个输入为图像Batch，对应尺寸为**（B,H,W,C）**，其中B为batch_size，H和W代表图像的宽高，C为通道数，需要注意的是，这边的通道数位于第三个维度，而torch直接读取的图像中通道位于第一个维度，因此需要对图片做预处理。第二个输入为窗口的尺寸。

if __name__ == '__main__':
    x = torch.randn(size=(1, 224, 224, 3))
    windows=window_partition(x=x, window_size=7)
    print(windows.shape)

结果

torch.Size([1024, 7, 7, 3])

4.3 window_reverse

def window_reverse(windows, window_size, H, W):
    """
    Args:
        windows: (num_windows*B, window_size, window_size, C)
        window_size (int): Window size
        H (int): Height of image
        W (int): Width of image
    Returns:
        x: (B, H, W, C)
    """
    B = int(windows.shape[0] / (H * W / window_size / window_size))
    x = windows.view(B, H // window_size, W // window_size, window_size, window_size, -1)
    x = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(B, H, W, -1)
    return x

对于上面呢的数据进行还原

if __name__ == '__main__':
    x = torch.randn(size=(1024, 7, 7, 3))
    windows=window_reverse(windows=x, window_size=7,H=224,W=224)
    print(windows.shape)

结果为

torch.Size([1, 224, 224, 3])

4.4 W-MSA

这一块就是W-MSA的实现，以及相对位置偏置的实现。什么是相对位置偏置？就是位置编码。所以Swin-Transformer的自注意力机制的公式如下：

class WindowAttention(nn.Module):
    def __init__(self, dim, window_size, num_heads, qkv_bias=True, qk_scale=None, attn_drop=0., proj_drop=0.):
        super().__init__()
        self.dim = dim
        self.window_size = window_size  # Wh, Ww
        self.num_heads = num_heads
        head_dim = dim // num_heads
        self.scale = qk_scale or head_dim ** -0.5
        self.relative_position_bias_table = nn.Parameter(
            torch.zeros((2 * window_size[0] - 1) * (2 * window_size[1] - 1), num_heads))  # 2*Wh-1 * 2*Ww-1, nH
        coords_h = torch.arange(self.window_size[0])
        coords_w = torch.arange(self.window_size[1])
        coords = torch.stack(torch.meshgrid([coords_h, coords_w]))  # 2, Wh, Ww
        coords_flatten = torch.flatten(coords, 1)  # 2, Wh*Ww
        relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :]  # 2, Wh*Ww, Wh*Ww
        relative_coords = relative_coords.permute(1, 2, 0).contiguous()  # Wh*Ww, Wh*Ww, 2
        relative_coords[:, :, 0] += self.window_size[0] - 1  # shift to start from 0
        relative_coords[:, :, 1] += self.window_size[1] - 1
        relative_coords[:, :, 0] *= 2 * self.window_size[1] - 1
        relative_position_index = relative_coords.sum(-1)  # Wh*Ww, Wh*Ww
        self.register_buffer("relative_position_index", relative_position_index)

        self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)
        self.attn_drop = nn.Dropout(attn_drop)
        self.proj = nn.Linear(dim, dim)
        self.proj_drop = nn.Dropout(proj_drop)

        trunc_normal_(self.relative_position_bias_table, std=.02)
        self.softmax = nn.Softmax(dim=-1)

    def forward(self, x, mask=None):
        B_, N, C = x.shape
        qkv = self.qkv(x).reshape(B_, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
        q, k, v = qkv[0], qkv[1], qkv[2]  # make torchscript happy (cannot use tensor as tuple)

        q = q * self.scale
        attn = (q @ k.transpose(-2, -1))

        relative_position_bias = self.relative_position_bias_table[self.relative_position_index.view(-1)].view(
            self.window_size[0] * self.window_size[1], self.window_size[0] * self.window_size[1], -1)  # Wh*Ww,Wh*Ww,nH
        relative_position_bias = relative_position_bias.permute(2, 0, 1).contiguous()  # nH, Wh*Ww, Wh*Ww
        attn = attn + relative_position_bias.unsqueeze(0)

        if mask is not None:
            nW = mask.shape[0]
            attn = attn.view(B_ // nW, nW, self.num_heads, N, N) + mask.unsqueeze(1).unsqueeze(0)
            attn = attn.view(-1, self.num_heads, N, N)
            attn = self.softmax(attn)
        else:
            attn = self.softmax(attn)

        attn = self.attn_drop(attn)

        x = (attn @ v).transpose(1, 2).reshape(B_, N, C)
        x = self.proj(x)
        x = self.proj_drop(x)
        return x

4.5 Patch Merging

Patch Merging在之前说过，它的主要目的就是将$H,W$降维，$C$升维

class PatchMerging(nn.Module):
    def __init__(self, input_resolution, dim, norm_layer=nn.LayerNorm):
        super().__init__()
        self.input_resolution = input_resolution
        self.dim = dim
        self.reduction = nn.Linear(4 * dim, 2 * dim, bias=False)
        self.norm = norm_layer(4 * dim)

    def forward(self, x):
        H, W = self.input_resolution
        B, L, C = x.shape
        assert L == H * W, "input feature has wrong size"
        assert H % 2 == 0 and W % 2 == 0, f"x size ({H}*{W}) are not even."

        x = x.view(B, H, W, C)

        x0 = x[:, 0::2, 0::2, :]  # B H/2 W/2 C
        x1 = x[:, 1::2, 0::2, :]  # B H/2 W/2 C
        x2 = x[:, 0::2, 1::2, :]  # B H/2 W/2 C
        x3 = x[:, 1::2, 1::2, :]  # B H/2 W/2 C
        x = torch.cat([x0, x1, x2, x3], -1)  # B H/2 W/2 4*C
        x = x.view(B, -1, 4 * C)  # B H/2*W/2 4*C

        x = self.norm(x)
        x = self.reduction(x)

        return x

4.6 Patch Embedding

Patch Embedding其实就是Patch Partition 和Linear Embedding，具体原理在开头已经讲明。

流程如下

• 第一步 使用二维卷积来实现patch embedding，embedding的维度就是卷积的输出通道。

  使用卷积层nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)，stride=patch_size这一步操作直接将输入的$(B,C,224,224)$图片分割成$\frac{224}{4}\times \frac{224}{4}$个$4\times 4$的patch,

  输入$[batch\_size,in\_channel,224,224]-->[batch\_size,out\_channel,56,56]$

• 第二步，把向量flatten后，进行转置

  $[B,C,ph,pw]-->[B,C,ph\times pw]-->[B,ph\times pw,C]$

  变成具体数字输入

  $[batch\_size,out\_channel,56,56]$

  $-->[batch\_size,out\_channel,56\times 56]$

  $-->[batch\_size,56\times 56,out\_channel]$

class PatchEmbed(nn.Module):
    r""" Image to Patch Embedding
    Args:
        img_size (int): Image size.  Default: 224.
        patch_size (int): Patch token size. Default: 4.
        in_chans (int): Number of input image channels. Default: 3.
        embed_dim (int): Number of linear projection output channels. Default: 96.
        norm_layer (nn.Module, optional): Normalization layer. Default: None
    """

    def __init__(self, img_size=224, patch_size=4, in_chans=3, embed_dim=96, norm_layer=None):
        super().__init__()
        img_size = to_2tuple(img_size)
        patch_size = to_2tuple(patch_size)
        patches_resolution = [img_size[0] // patch_size[0], img_size[1] // patch_size[1]]
        self.img_size = img_size
        self.patch_size = patch_size
        self.patches_resolution = patches_resolution
        self.num_patches = patches_resolution[0] * patches_resolution[1]

        self.in_chans = in_chans
        self.embed_dim = embed_dim

        self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)
        if norm_layer is not None:
            self.norm = norm_layer(embed_dim)
        else:
            self.norm = None

    def forward(self, x):
        B, C, H, W = x.shape
        # FIXME look at relaxing size constraints
        assert H == self.img_size[0] and W == self.img_size[1], 
            f"Input image size ({H}*{W}) doesn't match model ({self.img_size[0]}*{self.img_size[1]})."
        x = self.proj(x).flatten(2).transpose(1, 2)  # B Ph*Pw C
        if self.norm is not None:
            x = self.norm(x)
        return x

    def flops(self):
        Ho, Wo = self.patches_resolution
        flops = Ho * Wo * self.embed_dim * self.in_chans * (self.patch_size[0] * self.patch_size[1])
        if self.norm is not None:
            flops += Ho * Wo * self.embed_dim
        return flops

我们做一下测试

if __name__ == '__main__':
    x=torch.randn(size=(1,3,224,224))
    p=PatchEmbed(in_chans=3)
    out=p(x)
    print(out.shape)

结果

torch.Size([1, 3136, 96])

4.7 BasicLayer

首先是BasicLayer，这个是SWinTransformer的基本组成，相当于一个stage

class BasicLayer(nn.Module):
    def __init__(self, dim, input_resolution, depth, num_heads, window_size,
                 mlp_ratio=4., qkv_bias=True, qk_scale=None, drop=0., attn_drop=0.,
                 drop_path=0., norm_layer=nn.LayerNorm, downsample=None, use_checkpoint=False):

        super().__init__()
        self.dim = dim
        self.input_resolution = input_resolution
        self.depth = depth
        self.use_checkpoint = use_checkpoint

        # build blocks
        self.blocks = nn.ModuleList([
            SwinTransformerBlock(dim=dim, input_resolution=input_resolution,
                                 num_heads=num_heads, window_size=window_size,
                                 shift_size=0 if (i % 2 == 0) else window_size // 2,
                                 mlp_ratio=mlp_ratio,
                                 qkv_bias=qkv_bias, qk_scale=qk_scale,
                                 drop=drop, attn_drop=attn_drop,
                                 drop_path=drop_path[i] if isinstance(drop_path, list) else drop_path,
                                 norm_layer=norm_layer)
            for i in range(depth)])

        # patch merging layer
        if downsample is not None:
            self.downsample = downsample(input_resolution, dim=dim, norm_layer=norm_layer)
        else:
            self.downsample = None

    def forward(self, x):
        for blk in self.blocks:
            if self.use_checkpoint:
                x = checkpoint.checkpoint(blk, x)
            else:
                x = blk(x)
        if self.downsample is not None:
            x = self.downsample(x)
        return x

4.8 Swin Transformer

Swin Transformer一共有四个Stage块，如图(a)所示，这部分代码就是对于Stage块的实现。

1、获取宽度高度方向分别分成了几个patch

2、获取输入特征X的形状，由PatchEmbed和PatchMerging的输出可知，X的尺寸为（B ，H*W，C）

3、对X进行归一化，并转化形状为$(B,H,W,C)$

4、判断是否进行shifted，如果是则使用torch.roll对输入X的第1和第2维度进行循环移动。使用图像循环移动代替窗口移动，极大地减轻了算法的工程量！！！

5、进行窗口的分割，输入为移动后的X，输出为（nW*B, window_size, window_size, C）

进一步的调整窗口的形状为$(nW\ast B,window\_size\ast window\_size,C)$

7、对于每个子窗口计算局部注意力，尺寸为$(nW\ast B,window\_size\ast window\_size,C)$

进一步的调整窗口的形状为$(nW\ast B,window\_size，window\_size,C)$

8、将注意力的Batch还原为与图像batch数相同的尺寸$(B,H,W,C)$

9、如果第五步产生了图像循环移动，则此处对注意力进行相反方向的循环移动，移动距离与第五部相同

10、进行了DropPath的操作，对多分支网络进行随机剪枝，能够有效地增加网络的鲁棒性，也能避免过拟合。关于这个操作可以参考

class SwinTransformer(nn.Module):
    def __init__(self, img_size=224, patch_size=4, in_chans=3, num_classes=1000,
                 embed_dim=96, depths=[2, 2, 6, 2], num_heads=[3, 6, 12, 24],
                 window_size=7, mlp_ratio=4., qkv_bias=True, qk_scale=None,
                 drop_rate=0., attn_drop_rate=0., drop_path_rate=0.1,
                 norm_layer=nn.LayerNorm, ape=False, patch_norm=True,
                 use_checkpoint=False, **kwargs):
        super().__init__()

        self.num_classes = num_classes
        self.num_layers = len(depths)
        self.embed_dim = embed_dim
        self.ape = ape
        self.patch_norm = patch_norm
        self.num_features = int(embed_dim * 2 ** (self.num_layers - 1))
        self.mlp_ratio = mlp_ratio

        # split image into non-overlapping patches
        self.patch_embed = PatchEmbed(
            img_size=img_size, patch_size=patch_size, in_chans=in_chans, embed_dim=embed_dim,
            norm_layer=norm_layer if self.patch_norm else None)
        num_patches = self.patch_embed.num_patches
        patches_resolution = self.patch_embed.patches_resolution
        self.patches_resolution = patches_resolution

        # absolute position embedding
        if self.ape:
            self.absolute_pos_embed = nn.Parameter(torch.zeros(1, num_patches, embed_dim))
            trunc_normal_(self.absolute_pos_embed, std=.02)

        self.pos_drop = nn.Dropout(p=drop_rate)

        # stochastic depth
        dpr = [x.item() for x in torch.linspace(0, drop_path_rate, sum(depths))]  # stochastic depth decay rule

        # build layers
        self.layers = nn.ModuleList()
        for i_layer in range(self.num_layers):
            layer = BasicLayer(dim=int(embed_dim * 2 ** i_layer),
                               input_resolution=(patches_resolution[0] // (2 ** i_layer),
                                                 patches_resolution[1] // (2 ** i_layer)),
                               depth=depths[i_layer],
                               num_heads=num_heads[i_layer],
                               window_size=window_size,
                               mlp_ratio=self.mlp_ratio,
                               qkv_bias=qkv_bias, qk_scale=qk_scale,
                               drop=drop_rate, attn_drop=attn_drop_rate,
                               drop_path=dpr[sum(depths[:i_layer]):sum(depths[:i_layer + 1])],
                               norm_layer=norm_layer,
                               downsample=PatchMerging if (i_layer < self.num_layers - 1) else None,
                               use_checkpoint=use_checkpoint)
            self.layers.append(layer)

        self.norm = norm_layer(self.num_features)
        self.avgpool = nn.AdaptiveAvgPool1d(1)
        self.head = nn.Linear(self.num_features, num_classes) if num_classes > 0 else nn.Identity()

        self.apply(self._init_weights)

    def _init_weights(self, m):
        if isinstance(m, nn.Linear):
            trunc_normal_(m.weight, std=.02)
            if isinstance(m, nn.Linear) and m.bias is not None:
                nn.init.constant_(m.bias, 0)
        elif isinstance(m, nn.LayerNorm):
            nn.init.constant_(m.bias, 0)
            nn.init.constant_(m.weight, 1.0)

    @torch.jit.ignore
    def no_weight_decay(self):
        return {'absolute_pos_embed'}

    @torch.jit.ignore
    def no_weight_decay_keywords(self):
        return {'relative_position_bias_table'}

    def forward_features(self, x):
        x = self.patch_embed(x)
        if self.ape:
            x = x + self.absolute_pos_embed
        x = self.pos_drop(x)

        for layer in self.layers:
            x = layer(x)

        x = self.norm(x)  # B L C
        x = self.avgpool(x.transpose(1, 2))  # B C 1
        x = torch.flatten(x, 1)
        return x

    def forward(self, x):
        x = self.forward_features(x)
        x = self.head(x)
        return x

4.9 def flops

定义了计算计算复杂度用的公式

def flops(self):
        flops = 0
        flops += self.patch_embed.flops()
        for i, layer in enumerate(self.layers):
            flops += layer.flops()
        flops += self.num_features * self.patches_resolution[0] * self.patches_resolution[1] // (2 ** self.num_layers)
        flops += self.num_features * self.num_classes
        return flops

参考资料

Swin-Transformer网络结构详解_太阳花的小绿豆的博客-CSDN博客_swin transformer

swin-transformer详解及代码复现_apodxxx的博客-CSDN博客_swin transformer复现

SWinTransformer源码阅读笔记（三） - 知乎 (zhihu.com)

SWinTransformer源码阅读笔记（一） - 知乎 (zhihu.com)

SWinTransformer源码阅读笔记（二） - 知乎 (zhihu.com)

最后

以上就是执着眼神为你收集整理的2021-Swin TransformerSwin Transformer的全部内容，希望文章能够帮你解决2021-Swin TransformerSwin Transformer所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。