矩阵打印问题-zigzag打印矩阵

矩阵打印技巧：找到矩阵宏规律1，不要陷入细节，

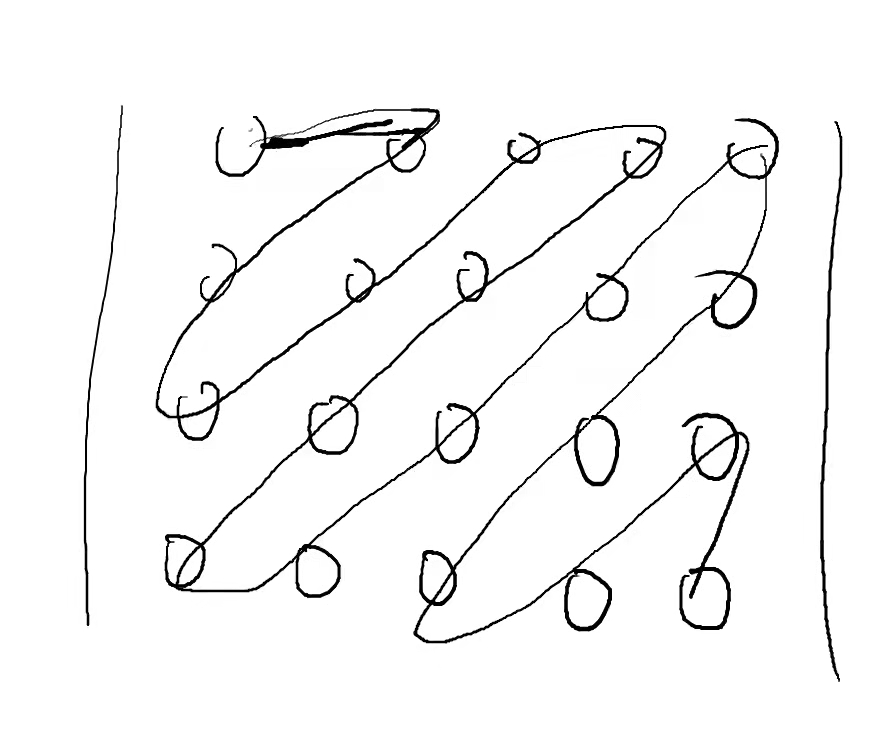
zigzag打印矩阵

1. 宏观的规律是什么 ？
   其实比较宏观的规律是都是打印斜线，只是方向不同而已(这个问题很容易解决)；

2. 如何实现宏观的规律？
   使用A[ar,ac]表示右上的点
   使用B[br,bc]表示左下的点

3. 这两个点如何移动呢？
   A点首先向右移动，直到无法向右移动时，向下移动
   B点首先向下移动，直到无法向下移动时，向右移动；

打印斜线的函数
A的坐标位(ar,ac),B的坐标位B(br,bc),
flag控制打印方向：true，从右上到左下打印，false 从左下到右上的打印；

void printLevel(int[][] matrix, int ar, int ac, int br, int bc, boolean flag) {
        // 右上到左下的打印
        if (flag) {
            while (ac >= bc) {
                System.out.print(matrix[ar][ac] + " ");
                ar++;
                ac--;
            }
            return;
        }
        //左下到右上的打印
        while (ac >= bc) {
            System.out.print(matrix[br][bc] + " ");
            br--;
            bc++;
        }

    }

打印矩形的函数
A的坐标位(ar,ac)：
A点 首先向右移动，直到不能向右移动，然后向下移动
B的坐标位B(br,bc)：
B点，首先向下移动，直到不能向右移动，燃火向右移动

针对特殊矩形也可以正常打印的：
例如:n * 1 单列矩阵，和1 * N 单行矩阵

private void printZigZag(int[][] matrix) {
        int rows = matrix.length;
        int col = matrix[0].length;

        int ar = 0, ac = 0;
        int br = 0, bc = 0;
        boolean flag = false;
        while (ar < rows) {
            printLevel(matrix, ar, ac, br, bc, flag);
            flag = !flag;
            //A点 首先向右移动，直到不能向右移动，然后向下移动
            ar = (ac == col - 1 ? ar + 1 : ar);
            ac = (ac == col - 1 ? ac : ac + 1);
            //B点，首先向下移动，直到不能向右移动，燃火向右移动
            bc = (br == rows - 1 ? bc + 1 : bc);
            br = (br == rows - 1 ? br : br + 1);
        }
        System.out.println("");
    }

最后

以上就是英俊草丛为你收集整理的矩阵打印问题-zigzag打印矩阵的全部内容，希望文章能够帮你解决矩阵打印问题-zigzag打印矩阵所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。