概述
1.线索二叉树
上一篇二叉树中，我们介绍了基本的二叉树的结构。每一个父节点对应两个子节点，左子节点和右子节点。其中我们会看到，很多节点的左右节点都为null，为了更高效的存储和遍历，我们考虑一种方式将这些为null的节点利用起来。这就是线索二叉树的思想，将为null的左子节点指向遍历时的前驱节点，为null的右子节点指向遍历时的后续节点。如此一来，在遍历的过程中，我们便可以直接通过左右子节点，找到叶子节点的前驱和后驱，使用一条线完整的将整刻树串起来。
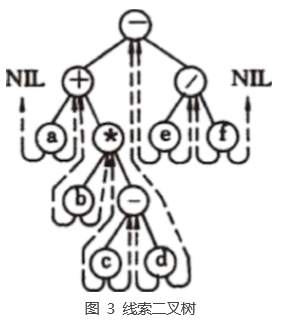
2.代码实现python
在实现的过程中，我们原来的Node类中需要添加两个标志位leftType和rightType.分别表示对应的节点是普通的子节点还是前驱后驱节点。实现过程如下：首先我们构建一棵树，然后使用中序遍历这树，使用pre变量记录前一个节点。对于当前节点左子节点为null的，将其左子节点指向pre节点；如果pre的右子节点也为null,将pre的右子节点指向当前节点；
然后进行遍历，先找到最下面的左子节点，如果该节点后后驱节点，则不断遍历其后驱节点。否则的话按照普通的中序遍历寻找下一个节点(),不断遍历直到找不到任何节点。则完成整棵树的遍历。
#-*- coding:utf-8 -*-
class Node(object):
def __init__(self,val):
self.val = val
self.left = None
self.right=None
# 左节点类型 0表示左子节点 1表示后驱
self.leftType = 0
# 右节点类型 0表示右子节点 1表示后驱
self.rightType = 0
def show(self):
print("遍历--当前节点为 = {}".format(self.val),end='t')
if self.left != None and self.leftType == 0:
print("左子节点为 = {}".format(self.left.val),end='t')
if self.right != None and self.rightType == 0:
print("右子节点为 = {}".format(self.right.val))
if self.left != None and self.leftType == 1:
print("前驱节点为 = {}".format(self.left.val),end='t')
if self.right != None and self.rightType == 1:
print("后驱节点为 = {}".format(self.right.val))
class ThreadTree(object):
def __init__(self):
self.root = None
self.pre = None
#构建一棵基本的树
def build(self,values):
# 将每个元素转换为node节点
nodes = [None if V is None else Node(V) for V in values]
# 给根节点添加左右子节点
for index in range(1, len(nodes)):
parent_index = (index - 1) // 2
parent = nodes[parent_index]
if parent is None:
raise Exception('parent node missing at index{}'.format(index))
if index % 2 == 0:
parent.right = nodes[index]
else:
parent.left = nodes[index]
self.root = nodes[0]
return nodes[0]
#在中序遍历的过程中对每个节点中left,right为null的进行复制前驱后驱节点
def threadedNode(self,node):
if node == None:
return
self.threadedNode(node.left)
# 处理当前节点的的前驱节点
if node.left == None:
node.left = self.pre
node.leftType = 1
print("当前节点={}".format(node.val))
if self.pre != None:
print("前驱结点为 = {}".format(self.pre.val))
if self.pre != None and self.pre.right == None:
# 前驱节点的右指针指向当前节点
self.pre.right = node
self.pre.rightType = 1
print("当前节点={},后驱结点为 = {}".format(self.pre.val, node.val))
self.pre = node
self.threadedNode(node.right)
def mid_order(self,node):
while node != None:
while node.leftType == 0:
node = node.left
if node != None:
node.show()
while node.rightType == 1:
node = node.right
node.show()
node = node.right
threadTree = ThreadTree()
node = threadTree.build([1,2,3,4,5,6,7,8])
threadTree.threadedNode(node)
threadTree.mid_order(node)3.线索二叉树总结
本文介绍了线索二叉树的原理及使用python实现的过程，最核心的思想就是利用了二叉树中为null的空指针，使这些指针指向前驱和后驱节点。
4.哈夫曼树
声明：本篇博客参考自哈夫曼树及其python实现。哈夫曼树又称为最优树、最优二叉树。其最优的体现就是使得所有节点的带权路径和最小，如图所示我们看到个节点中除了值之外，还有各自的权重信息。一个节点到另外一个节点所走过的节点称为路径，比如从根节点到c,需要经过50,29,14,6；带权路径长度是这么定义的:权重乘以其对应的路径数，比如下面图中的带权路径长度WPL为：9*2+12*2+15*2+6*3+3*4+5*4 = 122。我们的目标是使得带权路径长度最小，其实就是权重越大离根节点越近，这样保证总体的带权加和值最小。
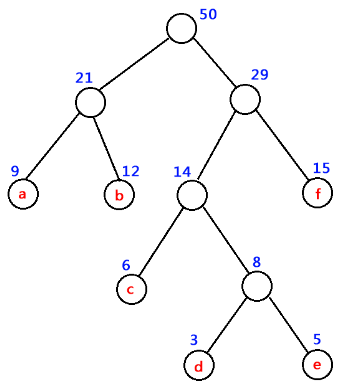
接下来我们介绍一下实现的算法：对权重列表进行排序，每次选中权重最小的两个节点作为左右子节点生成一棵树，将其权重之和作为该树的根节点。从权重列表中将这两个叶子节点删除，并且将根节点的权重加入权重列表。不断的迭代上面的过程，直到只有一个根节点为止，整棵树生成结束。
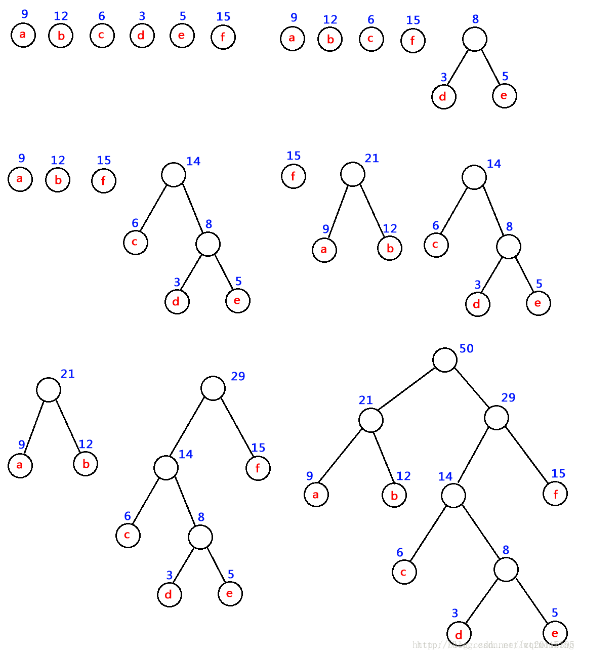
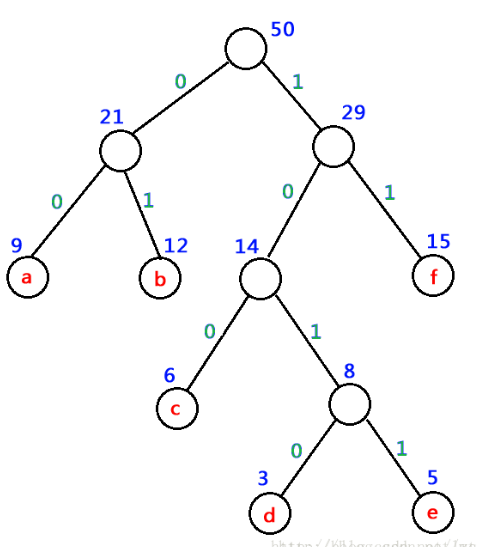
哈夫曼编码：哈夫曼树由于其带权路径长度最短，并且每个节点到根节点点的路径都是唯一的，可以用来进行编码。这是一种不等长的编码方式，在很大程度上节省了空间。
我们统计每个字在文本中出现的此处，作为其权重，构建一棵哈夫曼树，规定每棵子树的左分支路径为0，右分支路径为1。这样找到节点对应的路径，便可以沿着路径对其进行编码。比如下面的a可以编码为00，b可以编码为01；
5.python代码实现
#-*- coding:utf-8 -*-
#节点类
class Node(object):
def __init__(self,name=None,value=None):
self._name=name
self._value=value
self._left=None
self._right=None
#哈夫曼树类
class HuffmanTree(object):
#根据Huffman树的思想：以叶子节点为基础，反向建立Huffman树
def __init__(self,char_weights):
#将字典中所有的值 变成node数组
self.a=[Node(part[0],part[1]) for part in char_weights] #根据输入的字符及其频数生成叶子节点
while len(self.a)!=1:
#每次取权重最小的两个节点 生成父节点
#这两个节点分别为左右节点
self.a.sort(key=lambda node:node._value,reverse=True)
c=Node(value=(self.a[-1]._value+self.a[-2]._value))
c._left=self.a.pop()
c._right=self.a.pop()
self.a.append(c)
self.root=self.a[0]
self.b=list(range(10)) #self.b用于保存每个叶子节点的Haffuman编码,range的值只需要不小于树的深度就行
#用递归的思想生成编码
def huffmanEncode(self,tree,length):
node=tree
if (not node):
return
elif node._name:
print(node._name + '的编码为:',end='t')
for i in range(length):
print(self.b[i],end='t')
print ('n')
return
self.b[length]=0
self.huffmanEncode(node._left,length+1)
self.b[length]=1
self.huffmanEncode(node._right,length+1)
#生成哈夫曼编码
def get_code(self):
self.huffmanEncode(self.root,0)
if __name__=='__main__':
#输入的是字符及其频数
char_weights=[('a',5),('b',4),('c',10),('d',8),('f',15),('g',2)]
tree=HuffmanTree(char_weights)
tree.get_code()6.哈夫曼树总结
上面我们介绍了哈夫曼树，也称为最优二叉树。其根本的思想是使得带权路径之和最小，即权重越大的节点离根节点越近。实现算法的思路是，从权重列表中每次选择两个最小权重的节点为左右节点，其和作为根节点构成一棵树。然后从权重列表中删除这两个节点，并加入他们的和。不断的迭代直到只剩下一个根节点。然后我们介绍了哈夫曼树的实际应用之一，哈夫曼编码。规定左分支为0，右分支为1，通过节点的路径上所有分支的值生成编码。这是一种不等长，但是却能够保证节点唯一性的编码方式。大大的节省了空间。
7. 这天界，我守得，也杀得！
这天界，我守得，也杀得！我连着熬了三天两夜，终于把琉璃看完了。看完以后特别的伤心，就跟失恋了一样。真的太喜欢袁冰妍小姐姐了，那种可爱的笑容世界上再没有第二个。请允许我借用《洛神赋》中的几句诗表达我对小姐姐的仰慕：翩若惊鸿，婉若游龙。荣曜秋菊，华茂春松。髣髴兮若轻云之蔽月，飘飖兮若流风之回雪。谁能够让我见到她，你就是我这辈子最大的恩人。今天还有一个不好的消息就是，我喜欢了四年半的女神结婚了。唉！当然会很伤心了。不过这又能说明什么呢？只不过是这一段时间我需要用很多其它的东西，占满自己的思绪，避免一个人想太多留太多的泪！只不过在这一辈子短短的几十年中她不属于我而已，这么想的话就觉得人生还是过得下去的。对于别人的东西，我从来都不会再有什么期待。现在的我，只期待冰妍小姐姐的下一部电视剧。
琉璃·战神-我曾背负众生妄-燃虐向
最后
以上就是欢喜花瓣为你收集整理的常用数据结构之线索二叉树和哈夫曼树1.线索二叉树2.代码实现python3.线索二叉树总结4.哈夫曼树5.python代码实现6.哈夫曼树总结7. 这天界，我守得，也杀得！的全部内容，希望文章能够帮你解决常用数据结构之线索二叉树和哈夫曼树1.线索二叉树2.代码实现python3.线索二叉树总结4.哈夫曼树5.python代码实现6.哈夫曼树总结7. 这天界，我守得，也杀得！所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复