数据结构-图基础

判断题

1.用邻接矩阵法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关。

     T      F

2.在任一有向图中，所有顶点的入度之和等于所有顶点的出度之和。

     T      F

3.无论是有向图还是无向图，其邻接矩阵表示都是唯一的。

     T      F

选择题

1.下列关于无向连通图特征的叙述中，正确的是：

1. 所有顶点的度之和为偶数

2. 边数大于顶点个数减1

3. 至少有一个顶点的度为1

    A.只有1
    B.只有2
    C.1和2
    D.1和3

2.具有5个顶点的有向完全图有多少条弧？

    A.10
    B.16
    C.20
    D.25

共有n(n-1)条边。

3.在N个顶点的无向图中，所有顶点的度之和不会超过顶点数的多少倍？

    A.1
    B.2
    C.(N−1)/2
    D.N−1

4.具有N（N>0）个顶点的无向图至少有多少个连通分量？

    A.0
    B.1
    C.N−1
    D.N

5.具有N（N>0）个顶点的无向图至多有多少个连通分量？

    A.0
    B.1
    C.N−1
    D.N

6.一个有N个顶点的强连通图至少有多少条边？

    A.N−1
    B.N
    C.N+1
    D.N(N−1)

定义：图中任意一对顶点，既有从v_i到v_j的路径，也有从v_j到v_i的路径，则称该有向图是强连通图。

最少的情况是所有点围成一个圈。

7.如果G是一个有28条边的非连通无向图，那么该图顶点个数最少为多少？

    A.7
    B.8
    C.9
    D.10

8个顶点刚好构成连通完全无向图。增加一个顶点则是非连通无向图。

8.若无向图G =（V，E）中含10个顶点，要保证图G在任何情况下都是连通的，则需要的边数最少是：

    A.45
    B.37
    C.36
    D.9

任何情况下连通是指，边任意变动，都能保证G可以连通。

解法：先让n-1个点构成完全子图，然后把第n个顶点和这个子图相连，总共需要(n-1)(n-2)/2+1。

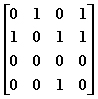
9.给定有向图的邻接矩阵如下：

顶点2（编号从0开始）的出度和入度分别是：

    A.3, 1
    B.1, 3
    C.0, 2
    D.2, 0

10.下列算法的功能是（）。

 typedef int adjmatrix[MaxVertexNum][MaxVertexNum];
void Graph1( adjmatrix G, int n)
{
//G是n个顶点的邻接矩阵存储结构的有向图
inti, j, d;
for(i = 0 ; i< n; i++)
{
d = 0;
for(j=0; j < n; j++)
if( G[i][j])
d++;
cout<<d<<endl;
}
}

    A.求G中各顶点的入度并输出
    B.求G中各顶点的出度并输出
    C.统计G的边数并输出
    D.求G中各顶点的度并输出

11.已知图G=（V，R），其中V={1,2,3,4,5,6,7}，R={(1,2),(1,3),(2,4),(3,4),(4,5),(4,6),(5,7),(6,7)}，如果采用邻接矩阵存储，则矩阵中有（ ）个非零个数。

    A.8
    B.7
    C.16
    D.14

12.具有 100 个顶点和 12 条边的无向图至多有多少个连通分量？

    A.87
    B.88
    C.94
    D.95

12条边，最多有可以有6个顶点，其余94个顶点各成一个连通分量。