数据结构与算法之线性表

一、线性表

1、定义

线性表（List）：由零个或多个元素组成的有序序列。

• 前驱元素：
  若A元素在B元素的前面，则称A为B的前驱元素。
• 后继元素：
  若B元素在A元素的后面，则称B为A的后继元素。

如果把线性表用数学语言来定义，则可以表示为(a1,…ai-1,ai,ai+1,…an)，ai-1领先于ai,ai领先于ai+1，称ai-1是ai的前驱元素，ai+1是ai的后继元素。
线性表根据数据存储方式可分为：顺序表和链表。

2、接口

package com.qiguangit.algorithm.linear;

public interface List<E> {
    // 添加元素
    boolean add(E e);
    // 在指定位置添加元素
    void add(int index, E element);
    // 设置指定位置的元素
    E set(int index, E element);
    // 获取指定位置的元素
    E get(int index);
    // 删除指定元素
    boolean remove(E element);
    // 删除指定位置的元素
    E remove(int index);
    // 清空线性表
    void clear();
    // 获取线性表的大小
    int size();
    // 判断线性表是否为空
    boolean isEmpty();
    // 找到指定元素的位置
    int indexOf(E element);
}

二、顺序表

顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构，一般情况下采用数组存储。在数组上完成数据的增删改查。
在Java中ArrayList就是顺序表，使用数组实现。

1、添加元素

添加元素时，我们需检查数组大小能否容纳新元素。如不能，则需要扩容（创建一个为当前数组两倍大小的新数组，并将所有元素移至新数组）。然后将新元素添加至数组尾部。

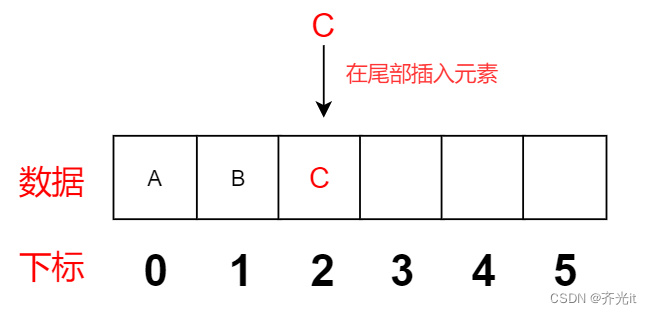
2、删除元素

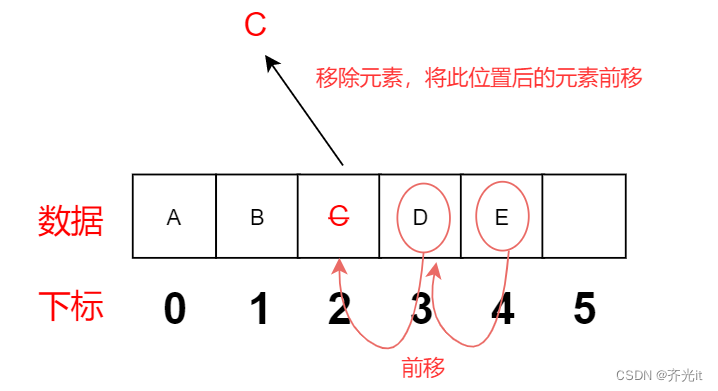
删除元素时，我们需要检查当前数组是否过大（若实际使用容量远远小于当前数组的大小，则会造成内存浪费）。若过大，则需进行缩容（如果我们发现数据元素的数量不足数组容量的1/4，则创建一个是原数组容量的1/2的新数组存储元素）。
删除指定位置元素后，将该位置后的元素前移。

3、简易实现

package com.qiguangit.algorithm.linear;

public class ArrayList<E> implements List<E> {

    private int size = 0;
    private Object[] elementData;

    public ArrayList(int capacity) {
        elementData = new Object[capacity];
    }

    @Override
    public boolean add(E e) {
        grow();
        elementData[size++] = e;
        return true;
    }

    @Override
    public void add(int index, E element) {
        grow();
        for (int i = size; i > index; i--) {
            elementData[i] = elementData[i-1];
        }
        elementData[index] = element;
        size++;
    }

    // 扩容
    private void grow() {
        if (size == elementData.length) {
            Object[] oldData = elementData;
            Object[] newData = new Object[size * 2];
            for (int i = 0; i < oldData.length; i++) {
                newData[i] = oldData[i];
            }
            elementData = newData;
        }
    }

    @Override
    public boolean remove(Object o) {
        int index = indexOf((E) o);
        return remove(index) != null;
    }

    @Override
    public E remove(int index) {
        if (index < 0 || index >= size) {
            return null;
        }

        // 缩容
        if (size < elementData.length / 4) {
            Object[] newElement = new Object[elementData.length / 2];
            for (int i = 0; i < size; i++) {
                newElement[i] = elementData[i];
            }
            elementData = newElement;
        }

        Object removeElement = elementData[index];
        for (int i = index; i < size; i++) {
            elementData[i] = elementData[i + 1];
        }
        size--;
        return (E) removeElement;
    }

    @Override
    public E set(int index, E element) {
        if (index >= size) {
            return null;
        }
        elementData[index] = element;
        return element;
    }
    
    @Override
    public E get(int index) {
        if (index >= size) {
            return null;
        }
        return (E) elementData[index];
    }

    @Override
    public int indexOf(E element) {
        for (int i = 0; i < size; i++) {
            if (elementData[i].equals(element)) {
                return i;
            }
        }
        return -1;
    }
    
    @Override
    public void clear() {
        size = 0;
    }

    @Override
    public int size() {
        return size;
    }

    @Override
    public boolean isEmpty() {
        return size == 0;
    }
}

顺序表在查询时效率高，但在插入和删除时，由于需要扩容与缩容，并伴随着元素移动。随着元素的增多，插入和删除的效率则大大降低。

三、链表

链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点（链表中每一个元素称为结点）组成，结点可以在运行时动态生成。
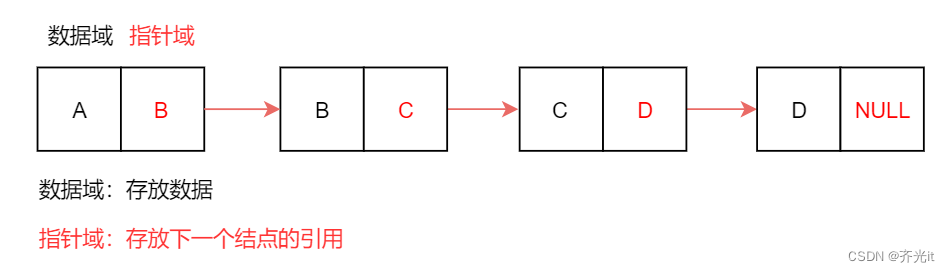
每个结点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域。
在Java中LinkedList就是链表。

1、添加元素

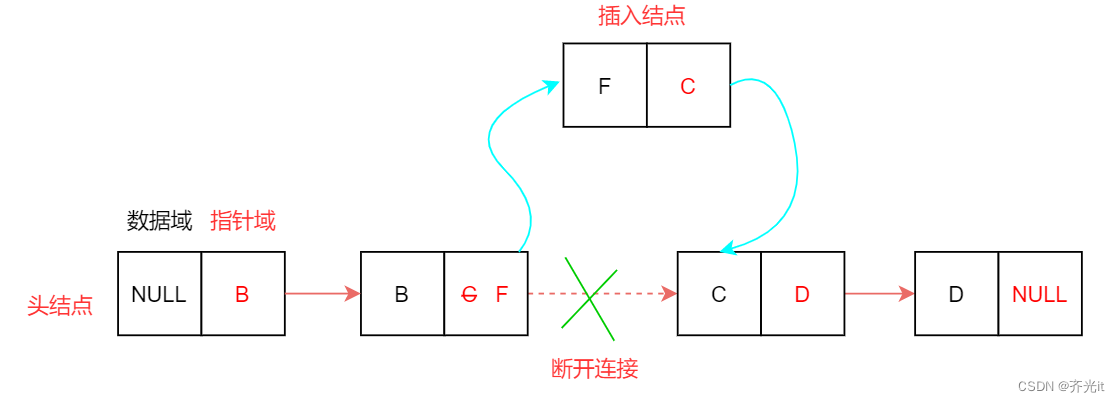
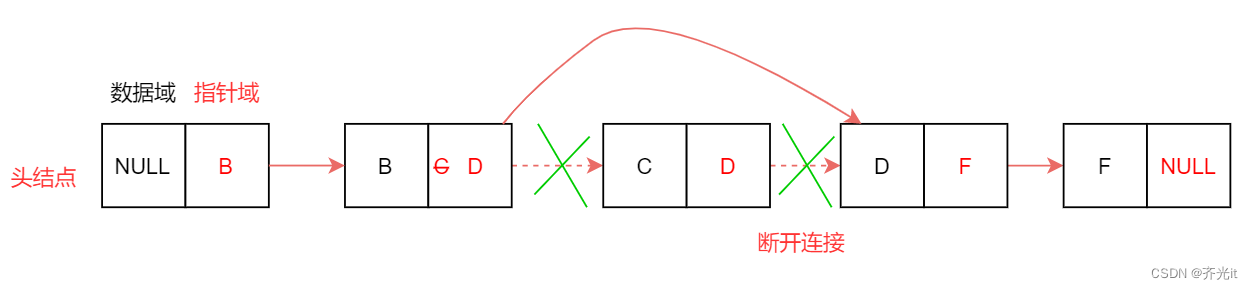
添加元素时，从头结点遍历，找到相应位置，断开当前结点与下一结点的连接，并指向新结点，新结点指向下一结点（当前结点指针域从存下一结点改成新结点，新结点指针域存放原下一结点）。
如：B结点指针域从C改成F，F结点的指针域改为C，则新结点F插入成功。

2、删除元素

删除元素时，从头结点遍历，找到相应位置，将当前结点指向下一结点的下一结点。
如：B结点的指针域从C改成D，C结点则被删除。

3、简易实现

package com.qiguangit.algorithm.linear;

public class LinkedList<E> implements List<E> {

    private Node<E> head;
    private int size;

    public LinkedList() {
        head = new Node<>();
    }

    @Override
    public boolean add(E e) {
        final Node<E> newNode = new Node<>(e, null);
        Node<E> h = head;
        while (h.next != null) {
            h = h.next;
        }
        h.next = newNode;
        size++;
        return true;
    }

    @Override
    public void add(int index, E element) {
        if (index < 0 || index >= size) {
            return;
        }

        Node<E> h = head;
        for (int i = 0; i <= index - 1; i++) {
            h = h.next;
        }

        final Node<E> newNode = new Node<>(element, null);
        final Node<E> next = h.next;
        h.next = newNode;
        newNode.next = next;
        size++;
    }

    @Override
    public boolean remove(Object o) {
        int i = indexOf((E) o);
        E remove = remove(i);
        return remove != null;
    }

    @Override
    public E remove(int index) {
        if (index < 0 || index >= size) {
            return null;
        }

        Node<E> h = head;
        for (int i = 0; i <= index - 1; i++) {
            h = h.next;
        }
        Node<E> next = h.next;
        h.next = h.next.next;
        size--;
        return next.element;
    }

    @Override
    public E set(int index, E element) {
        if (index < 0 || index >= size) {
            return null;
        }

        Node<E> h = head;
        for (int i = 0; i <= index; i++) {
            h = h.next;
        }
        h.element = element;
        return element;
    }

    @Override
    public E get(int index) {
        if (index < 0 || index >= size) {
            return null;
        }

        Node<E> h = head;
        for (int i = 0; i <= index; i++) {
            h = h.next;
        }
        return h.element;
    }

    @Override
    public void clear() {
        size = 0;
        head.next = null;
    }

    @Override
    public int size() {
        return size;
    }

    @Override
    public boolean isEmpty() {
        return size == 0;
    }

    @Override
    public int indexOf(E element) {
        Node<E> h = head;
        int i = 0;
        while (h.next != null) {
            h = h.next;
            if (h.element == element) {
                return i;
            }
            i++;
        }
        return -1;
    }

    // 结点类
    private static class Node<E> {
        // 数据域
        public E element;
        // 指针域
        public Node<E> next;

        public Node() {
        }

        public Node(E element, Node<E> next) {
            this.element = element;
            this.next = next;
        }
    }
}

链表在插入和删除时效率很高，只需更改结点间的引用，即可完成。但查询则效率较低，需要从头结点遍历，在极端情况下，需要遍历整个链表才能找到相应元素。

最后

以上就是酷炫滑板为你收集整理的数据结构与算法之线性表的全部内容，希望文章能够帮你解决数据结构与算法之线性表所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。