线性表之链式存储结构
链式存储结构
- 定义:每个数据元素都有后继元素的存储地址
- 相关概念:
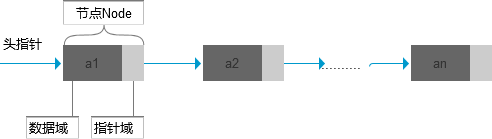
- 节点(Node):数据域和指针域组成的数据元素
- 所需属性:
- 数据域:存储数据元素数据的域
- 指针域:存储后继元素位置的域
图形:
无头节点的链式结构
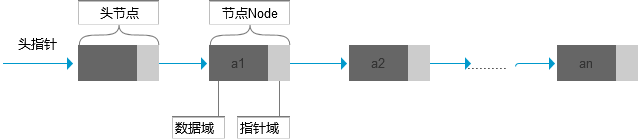
有头节点的链式结构
代码实现:
public class LinkList<E> { private Node firstNode; class Node<E> { private E data; private Node next; } }
链式结构与顺序结构
- 存储分配方式:
- 顺序结构是连续的存储单元
- 链式结构是任意位置的存储单元
- 时间性能:
- 查找:
- 顺序存储结构 O(1)
- 单链表 O(n)
- 插入和删除:
- 顺序结构:需要平均移动表长一半的元素 O(n)
- 单链表:知道位置时,插入和删除为 O(1)
- 查找:
- 空间性能:
- 顺序结构:需要预分配存储空间,分大了会浪费,分小了易溢出
- 单链表:不受存储空间的限制
操作
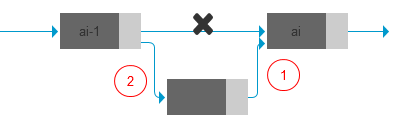
插入节点
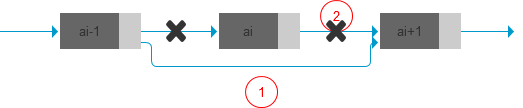
删除节点
代码实现
插入
- 插入首节点做特殊处理
- 寻找到插入位置 i,并做判断是否符合插入条件
将新节点的 next 指向 i,然后 i-1 的 next 指向新节点
public boolean insert(int i, E element) { if(i == 0) { insertFirst(element); return true; } int j = 1; Node node = this.firstNode; while (node != null && j < i){ node = node.next; j++; } if (node == null || j > i) throw new IndexOutOfBoundsException("下标: " + i + ",链表长度: " + this.length); Node<E> newNode = new Node<>(element); newNode.next = node.next; node.next = newNode; this.length++; return true; }
删除
- 删除首节点做特殊处理
- 寻找到删除位置 i,并判断是否满足删除条件
- 将要删除的节点的数据保存起来
将 i-1 的 next 指向 i+1,然后释放要删除的节点 i
public E delete(int i) { if(i == 0 && this.firstNode != null){ return deleteFirst(); } int j = 1; Node node = this.firstNode; while(node != null && j < i){ node = node.next; j++; } if(node == null || node.next == null) throw new IndexOutOfBoundsException("下标: " + i + ",链表长度: " + this.length); Node<E> deNode = node.next; E element = deNode.data; node = deNode.next; deNode.next = null; deNode.data = null; this.length--; return element; }
说明
- 除了单链表还有:静态链表、循环链表、双向链表
- 代码还可以做很多优化,主要是了解单链表的特性
- gihub源码链接 源码还有获取元素和在末尾添加元素的操作
最后
以上就是感性棒球最近收集整理的关于4_线性表_链式存储线性表之链式存储结构的全部内容,更多相关4_线性表_链式存储线性表之链式存储结构内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复