统计学小知识-什么是qqplot

最近读文章遇到qqplot的问题，看了几个视频讲解，大致有了个了解

首先我们需要了解什么是 quantile :

从这个视频里有个大概了解：https://www.youtube.com/watch?v=IFKQLDmRK0Y

quantile – median – it splits the data into equal sized groups. 50% quantile

如果我们将数据分为4个大小相等的组，则25％的分位数表示25％的数据点小于它。

Quantile 就是把样本区分成相同大小的组分.

我们也可以根据样本来划分quantile，见下面的图例：

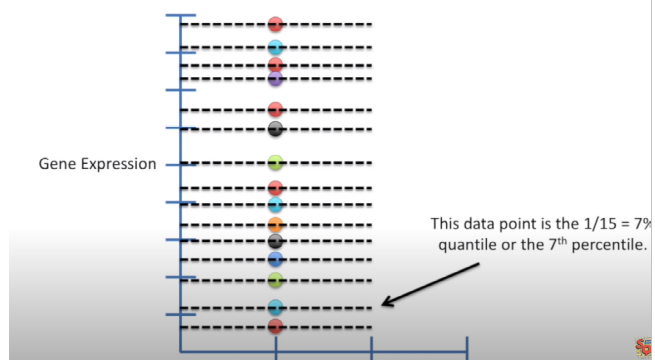
在R中，分位数函数有9种计算方法，如果您的数据集很大，那么所有方法都将得出非常相似的结果，数据集合小则反之。

第二，什么是正态分布
https://www.youtube.com/watch?v=rzFX5NWojp0
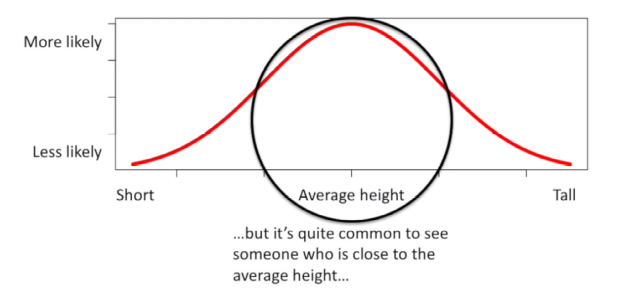
正态分布（也称为高斯分布）是关于均值对称的概率分布，这表明均值附近的数据比不均值的数据更频繁地出现。 在图形形式中，正态分布将显示为钟形曲线。
-例如以下

x

根据正态分布的特点我们知道均值+/-2个标准差之间代表了95%的数据，这个例子左侧是婴儿身高分布，右边是成人身高分布，它们都是正态分布

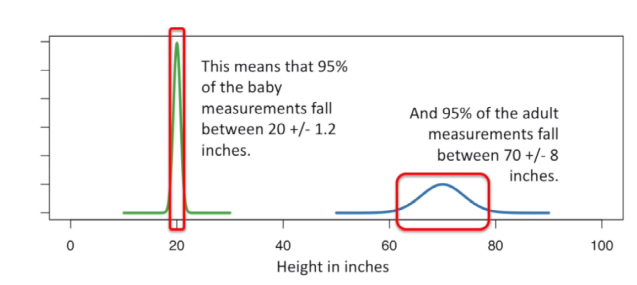
下面讲下什么是qq plot - 全称是quantile-quantile plot，可以用来检测一个分布是否符合正态分布、均匀分布.... https://www.youtube.com/watch?v=X9_ISJ0YpGw

比如我们有一组数字 3.89 3.99 4.5 6.7 6.8 8.7 9.5 10.2 12.5 （9个数字）检测是否符合正态分布

根据我们上面的定义 3.89对应的是1/10 quantile，3.4对应的第二个1/10quantile，我们把正态分布均分成10等分，得到下图,对应1/10的z score是-1.28

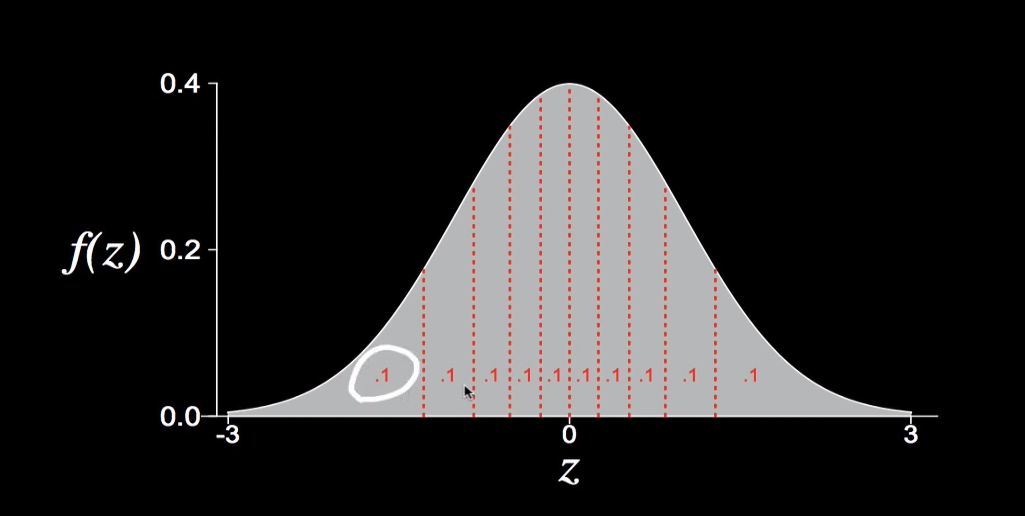
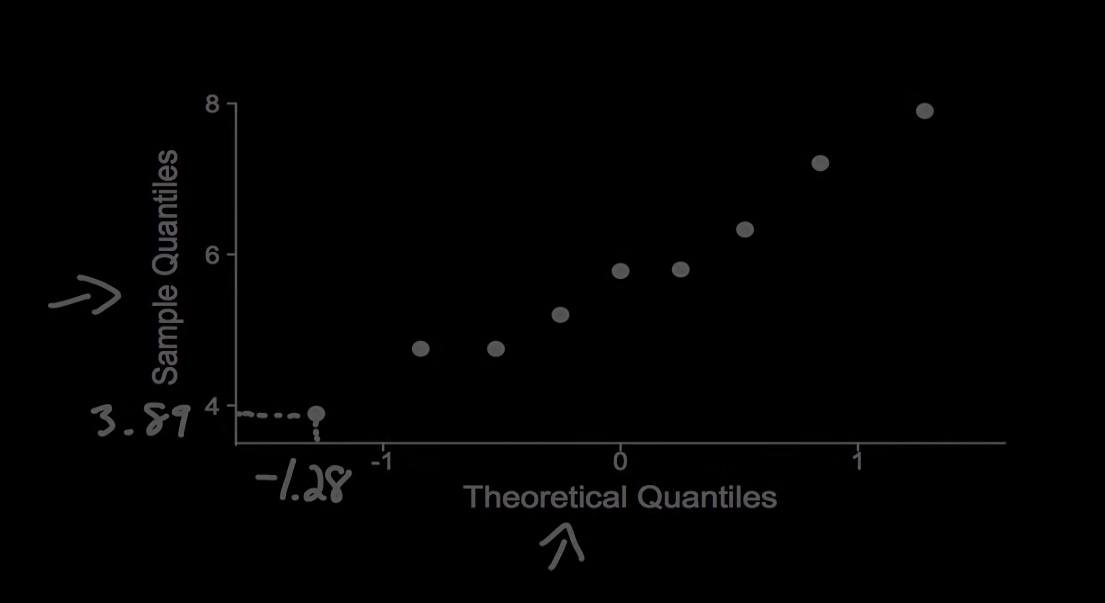
把对应的z score填写为x轴，对应的实际轴为y轴就可以得到qqplot图

如果大多数的点都在线上，就可以说明大致符合正态分布 

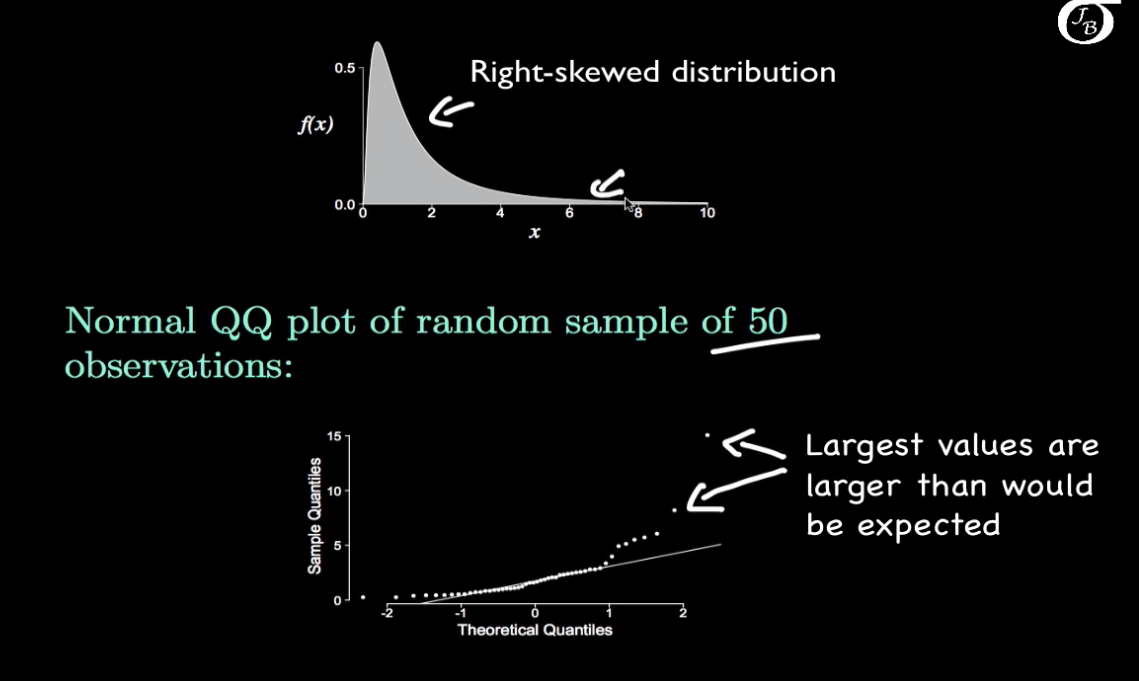
qqplot的x y轴可以互换，下面是一些例子

比如这种负偏分布，与划线的正态分布相比，我们在小的值里，实际值并不能得到比理论分布那么小的值，因为它没有尾巴，很快就停止了，相反在大的值里得到比我们期望的更大的值，因为尾巴更长。

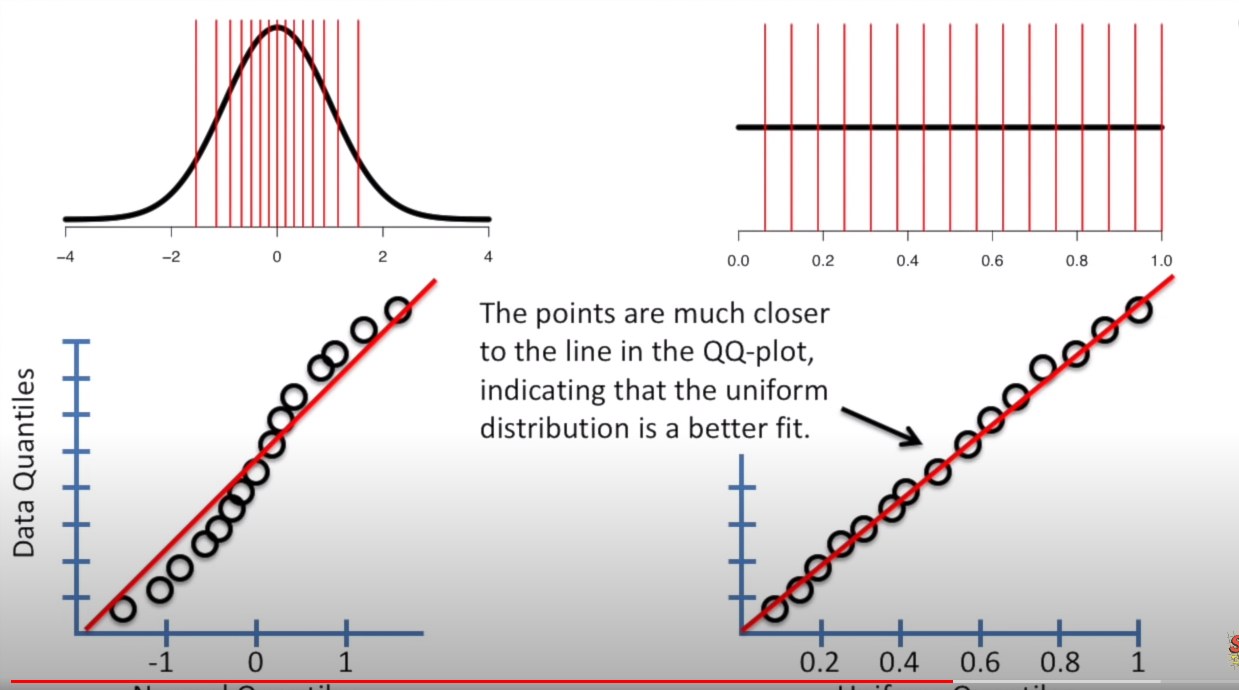
另外，qqplot不仅仅可以用于正态分布检验，也可以用于uniform 等其他分布的检验 

https://www.youtube.com/watch?v=okjYjClSjOg

参考资料 

https://www.youtube.com/watch?v=IFKQLDmRK0Y

https://www.youtube.com/watch?v=rzFX5NWojp0

https://www.youtube.com/watch?v=X9_ISJ0YpGw

https://www.youtube.com/watch?v=okjYjClSjOg

最后

以上就是伶俐小蘑菇为你收集整理的统计学小知识-什么是qqplot的全部内容，希望文章能够帮你解决统计学小知识-什么是qqplot所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。