啥是递推算法？
递推法是一种重要的数学方法，在数学的各个领域中都有广泛的运用，也是计算机用于数值计算的一个重要算法。这种算法特点是：一个问题的求解需一系列的计算，在已知条件和所求问题之间总存在着某种相互联系的关系，在计算时，如果可以找到前后过程之间的数量关系（即递推式），那么，从问题出发逐步推到已知条件，此种方法叫逆推。无论顺推还是逆推，其关键是要找到递推式。这种处理问题的方法能使复杂运算化为若干步重复的简单运算，充分发挥出计算机擅长于重复处理的特点。
递推算法的首要问题是得到相邻的数据项间的关系（即递推关系）。递推算法避开了求通项公式的麻烦，把一个复杂的问题的求解，分解成了连续的若干步简单运算。一般说来，可以将递推算法看成是一种特殊的迭代算法。
题目举例
1.数字三角形
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14如下所示为一个数字三角形。请编一个程序计算从顶到底的某处的一条路径，使该路径所经过的数字总和最大。只要求输出总和。 1、 一步可沿左斜线向下或右斜线向下走； 2、 三角形行数小于等于100； 3、 三角形中的数字为0，1，…，99； 测试数据通过键盘逐行输入，如上例数据应以如下所示格式输入： 5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5 【算法分析】 此题解法有多种，从递推的思想出发，设想，当从顶层沿某条路径走到第i层向第i+1层前进时，我们的选择一定是沿其下两条可行路径中最大数字的方向前进，为此，我们可以采用倒推的手法，设a[i][j]存放从i,j 出发到达n层的最大值，则a[i][j]=max{a[i][j]+a[i+1][j]，a[i][j]+a[i+1][j+1]}，a[1][1] 即为所求的数字总和的最大值。
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19#include<iostream> using namespace std; int main() { int n,i,j,a[101][101]; cin>>n; for (i=1;i<=n;i++) for (j=1;j<=i;j++) cin>>a[i][j]; //输入数字三角形的值 for (i=n-1;i>=1;i--) for (j=1;j<=i;j++) { if (a[i+1][j]>=a[i+1][j+1]) a[i][j]+=a[i+1][j]; //路径选择 else a[i][j]+=a[i+1][j+1]; } cout<<a[1][1]<<endl; }
2.Fibonacci数列
复制代码
1
2
3
4
5
6满足F1=F2=1，Fn=Fn-1+Fn-2的数列称为斐波那契数列（Fibonacci），它的前若干项是1，1，2，3，5，8，13，21，34……求此数 列第n项（n>=3）。 即： f1=1 （n=1） f2=1 （n=2） fn=fn-1 + fn-2 （n>=3）
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19#include<iostream> #include<cstdio> using namespace std; int main() { int f0=1,f1=1,f2; int n; cin>>n; for (int i=3; i<=n; ++i) { f2=f0+f1; f0=f1; f1=f2; } printf("%dn",f2); return 0; }
3.多米诺骨牌排列
复制代码
1
2有 2χn的一个长方形方格，用一个1*2的骨牌铺满方格。
复制代码
1
2
3
4
5
6编写一个程序，试对给出的任意一个n(n>0), 输出铺法总数。 【算法分析】 （1）面对上述问题，如果思考方法不恰当，要想获得问题的解答是相当困难的。可以用递推方法归纳出问题解的一般规律。 （2）当n=1时，只能是一种铺法，铺法总数有示为x1=1。 （3）当n=2时：骨牌可以两个并列竖排，也可以并列横排，再无其他方法，如下左图所示，因此，铺法总数表示为x2=2；
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13（4）当n=3时：骨牌可以全部竖排，也可以认为在方格中已经有一个竖排骨牌，则需要在方格中排列两个横排骨牌（无重复方法），若已经在方格中排列两个横排骨牌，则必须在方格中排列一个竖排骨牌。如上右图，再无其他排列方法，因此铺法总数表示为x3=3。 由此可以看出，当n=3时的排列骨牌的方法数是n=1和n=2排列方法数的和。 （5）推出一般规律：对一般的n，要求xn可以这样来考虑，若第一个骨牌是竖排列放置，剩下有n-1个骨牌需要排列，这时排列方法数为xn-1；若第一个骨牌是横排列，整个方格至少有2个骨牌是横排列（1*2骨牌），因此剩下n-2个骨牌需要排列，这是骨牌排列方法数为xn-2。从第一骨牌排列方法考虑，只有这两种可能，所以有： xn=xn-1+xn-2 （n>2） x1=1 x2=2 xn=xn-1+xn-2就是问题求解的递推公式。任给n都可以从中获得解答。例如n=5， x3=x2+x1=3 x4=x3+x2=5 x5=x4+x3=8
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18#include<iostream> using namespace std; int main() { int n,i,j,a[101]; cout<<"input n:"; //输入骨牌数 cin>>n; a[1]=1;a[2]=2; cout<<"x[1]="<<a[1]<<endl; cout<<"x[2]="<<a[2]<<endl; for (i=3;i<=n;i++) //递推过程 { a[i]=a[i-1]+a[i-2]; cout<<"x["<<i<<"]="<<a[i]<<endl; } } //问题的结果就是斐波那契数。
4.昆虫繁殖
复制代码
1
2
3
4
5
6
7
8
9
10
11【问题描述】 科学家在热带森林中发现了一种特殊的昆虫，这种昆虫的繁殖能力很强。每对成虫过x个月产y对卵，每对卵要过两个月长成成虫。假设每个成虫不死，第一个月只有一对成虫，且卵长成成虫后的第一个月不产卵(过X个月产卵)，问过Z个月以后，共有成虫多少对？0=<X<=20,1<=Y<=20,X=<Z<=50 【输入格式】 x,y,z的数值 【输出格式】 过Z个月以后，共有成虫对数 【输入样例】 1 2 8 【输出样例】 37
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17#include<iostream> using namespace std; int main() { long long a[101]={0},b[101]={0},i,j,x,y,z; cin>>x>>y>>z; for(i=1;i<=x;i++){a[i]=1;b[i]=0;} for(i=x+1;i<=z+1;i++) //因为要统计到第z个月后，所以要for到z+1 { b[i]=y*a[i-x]; a[i]=a[i-1]+b[i-2]; } cout<<a[z+1]<<endl; return 0; }
5.位数问题
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28【问题描述】 在所有的N位数中，有多少个数中有偶数个数字3？由于结果可能很大，你只需要输出这个答案对12345取余的值。 【输入格式】 读入一个数N 【输出格式】 输出有多少个数中有偶数个数字3。 【输入样例】 2 【输出样例】 73 【数据规模】 1<=N<=1000 【样例说明】 在所有的2位数字，包含0个3的数有72个，包含2个3的数有1个，共73个 【算法分析】 方法一：排列组合(但需要运用动态规划)。 可以列出公式,在n个格子中放x个3(其中x为偶数,包括0).。 c(n,x)*9^(n-x)-c(n-1,x)*9^(n-x-1) 含义为在n个格子中取x个3,且不考虑第一位的特殊情况为c(n,x)*9^(n-x)。 而第一位为0的情况,为c(n-1,x)*9^(n-x-1),两者减下,就为答案。 方法二：递推 考虑这种题目,一般来说都是从第i-1位推导第i位,且当前位是取偶数还是取奇数的。 恍然大悟.可以用f[i][0]表示前i位取偶数个3有几种情况,f[i][1]表示前i位取奇数个3有几种情况。 则状态转移方程可以表示为: f[i][0]=f[i-1][0]*9+f[i-1][1];f[i][1]=f[i-1][0]+f[i-1][1]*9; 边界条件:f[1][1]=1;f[1][0]=9;
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18#include<iostream> using namespace std; int main() { int f[1001][2],n,i,x; cin>>n; f[1][1]=1;f[1][0]=9; for(i=2;i<=n;i++) { x=f[1][0]; if(i==n)x--; f[i][0]=(f[i-1][0]*x+f[i-1][1])%12345; f[i][1]=(f[i-1][1]*x+f[i-1][0])%12345; } cout<<f[n][0]; return 0; }
6.过河卒
复制代码
1
2
3
4
5
6棋盘上A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下、或者向右。同时在棋盘上的任一点有一个对方 的马（如C点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点，如图3-1中的C点和P1，……，P8，卒不能 通过对方马的控制点。棋盘用坐标表示，A点(0,0)、B点(n, m) (n,m为不超过20的整数),同样马的位置坐标是需要给 出的，C≠A且C≠B。现在要求你计算出卒从A点能够到达B点的路径的条数。
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
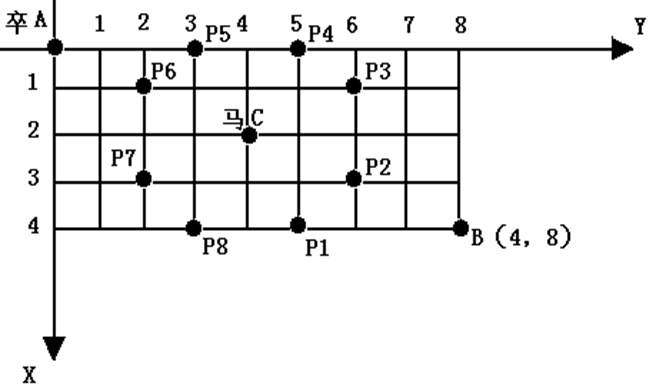
14【算法分析】 跳马是一道老得不能再老的题目，我想每位编程初学者都学过，可能是在学回溯或搜索等算法的时候，很多书上也有类似的题目，一些比赛中也出现过这一问题的变形（如NOIP1997初中组的第三题）。有些同学一看到这条题目就去搜索，即使你编程调试全通过了，运行时你也会发现：当n,m=15就会超时。 其实，本题稍加分析就能发现，要到达棋盘上的一个点，只能从左边过来（我们称之为左点）或是从上面过来（我们称之为上点），所以根据加法原理，到达某一点的路径数目，就等于到达其相邻的上点和左点的路径数目之和，因此我们可以使用逐列（或逐行）递推的方法来求出从起点到终点的路径数目。障碍点（马的控制点）也完全适用，只要将到达该点的路径数目设置为0即可。 用F[i][j]表示到达点(i,j)的路径数目，g[i][j]表示点(i, j)有无障碍，g[i][j]=0表示无障碍，g[i][j]=1表示有障碍。 则，递推关系式如下： F[i][j] = F[i-1][j] + F[i][j-1] //i>0且j>0且g[i][j]= 0 递推边界有4个： F[i][j] = 0 //g[i][j] = 1 F[i][0] = F[i-1][0] //i > 0且g[i][0] = 0 F[0][j] = F[0][j-1] //j > 0且g[0][j] = 0 F[0][0] = 1 考虑到最大情况下：n=20,m=20，路径条数可能会超过231-1,所以要用高精度。
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30#include <iostream> #include <cstring> using namespace std; int xi[9]={0,-2,-1,1,2,2,1,-1,-2}, yi[9]={0,1,2,2,1,-1,-2,-2,-1}; unsigned long long a[21][21],n,m,x,y,i,j; bool map[21][21]; int main() { cin>>n>>m>>x>>y; for(int i=1;i<=8;i++) { if(xi[i]+x>=0&&xi[i]+x<=20&&yi[i]+y>=0&&yi[i]+y<=20) map[xi[i]+x][yi[i]+y]=1; } map[x][y]=1; for(i=0;i<=20;i++) {if(map[0][i]==1){a[0][i]=0;break;}a[0][i]=1;} for(i=0;i<=20;i++) {if(map[i][0]==1){a[i][0]=0;break;}a[i][0]=1;} for(i=1;i<=n;i++) for(j=1;j<=m;j++) { if(map[i][j]==1)a[i][j]=0; else a[i][j]=a[i-1][j]+a[i][j-1]; } cout<<a[n][m]; return 0; }
7.走楼梯
复制代码
1
2
3
4
5
6楼梯有N级台阶，上楼可以一步上一阶，也可以一步上二阶。编一递归程序，计算共有多少种不同走法？ 【输入样例】Stairs.in 3 【输出样例】Stairs.out 3
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14#include<iostream> using namespace std; int main() { int n,a=1,b=1,c; cin>>n; for(int i=3;i<=n;i++) { c=a+b; a=b; b=c; } cout<<c<<endl; }
8.兔子繁殖
复制代码
1
2
3
4
5
6
7
8
9
10有一种兔子，出生后一个月就可以长大，然后再过一个月一对长大的兔子就可以生育一对小兔子且以后每个月都能生育一对。现在，我们有一对刚出生的这种兔子，那么，n个月过后，我们会有多少对兔子呢？假设所有的兔子都不会死亡。 【输入格式】 输入文件仅一行，包含一个自然数n。 【输出格式】 输出文件仅一行，包含一个自然数，即n个月后兔子的对数。 【输入样例】Rabbit.in 5 【输出样例】Rabbit.out 5
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16//稍微一看就能看看出是斐波那契 #include<iostream> using namespace std; int main(){ int n; cin >> n; int a[n + 10]; a[0] = 1; a[1] = 1; for (int i = 2; i < n; i++) { a[i] = a[i - 1] + a[i - 2]; } cout << a[n - 1]; return 0; }
9.平面分割
复制代码
1
2
3
4
5
6
7
8
9
10同一平面内有n（n≤500）条直线，已知其中p（p≥2）条直线相交于同一点，则这n条直线最多能将平面分割成多少个不同的区域？ 【输入格式】 两个整数n（n≤500）和p（2≤p≤n）。 【输出格式】 一个正整数，代表最多分割成的区域数目。 【输入样例】Surface.in 12 5 【输出样例】Surface.out 73
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23#include<iostream> #include<algorithm> #include <vector> #include <fstream> #include <string> #include <set> using namespace std; #define maxn 1000000 int ans[maxn]; int main() { int n; cin>>n; ans[1]=2; for(int i=2;i<=n;i++) { ans[i]=ans[i-1]+i; } cout<<ans[n]; return 0; }
10.蜜蜂路线
复制代码
1
2
3【问题描述】 一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你：蜜蜂从蜂房M开始爬到蜂房N，M<N，有多少种爬行路线？
复制代码
1
2
3
4
5
6
7
8
9
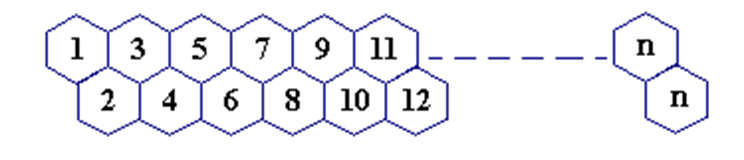
10【输入格式】 输入M，N的值。 【输出格式】 爬行有多少种路线。 【输入样例】bee.in 1 14 【输出样例】bee.out 377
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18#include <iostream> #define SIZE 15001 using namespace std; int a[SIZE] = {0, 1}; int main() { int n, m, i; cin >> m >> n; n -= m; n++; for (i = 2; i <= n; i++) { a[i] = a[i-1] + a[i-2]; } cout << a[n] << endl; return 0; }
11.数塔问题
复制代码
1
2
3【问题描述】 设有一个三角形的数塔，顶点为根结点，每个结点有一个整数值。从顶点出发，可以向左走或向右走，如图所示：
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
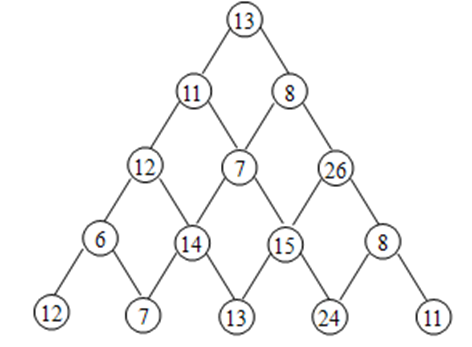
17若要求从根结点开始，请找出一条路径，使路径之和最大，只要输出路径的和。 【输入格式】 第一行为n(n<10)，表示数塔的层数 从第2行至n+1行，每行有若干个数据，表示数塔中的数值。 【输出格式】 输出路径和最大的路径值。 【输入样例】tower.in 5 13 11 8 12 7 26 6 14 15 8 12 7 13 24 11 【输出样例】tower.out 86
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25#include <bits/stdc++.h> using namespace std; int mountain[MAXN][MAXN]; int dp[MAXN + 1][MAXN + 1]; int main() { cin>>n; for (int i = 0; i < N; ++i) { for (int j = 0; j <= i; ++j) cin>>mountain[i][j]; } for (int i = N - 1; i >= 0; --i) { for (int j = 0; j <= i; ++j) { dp[i][j] = max(dp[i + 1][j], dp[i + 1][j + 1]) + mountain[i][j]; } } cout<<dp[0][0]<<endl; }
12.极值问题
复制代码
1
2
3
4
5
6
7
8
9
10
11【问题描述】 已知m、n为整数，且满足下列两个条件： ① m、n∈{１，２，…，k}，即1≤m，n≤k ②（n2－m*n－m2）2＝1 你的任务是：编程输入正整数k（1≤k≤109），求一组满足上述两个条件的m、n，并且使m2＋n2的值最大。例如，从键盘输入k=1995，则输出：m=987 n=1597。 【输入样例】Acme.in 1995 【输出样例】Acme.out m=987 n=1597
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37//答案就是一个斐波那契数列，求出<=k的最大的相邻两项即可 #include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<cstdlib> #include<ctime> using namespace std; inline int read() { int ans = 0,op = 1; char ch = getchar(); while(ch < '0' || ch > '9') { if(ch == '-') op = -1; ch = getchar(); } while(ch >= '0' && ch <= '9') { (ans *= 10) += ch - '0'; ch = getchar(); } return ans * op; } typedef int mainint; #define int long long int a,b,c,k; mainint main() { k = read(); a = b = 1; c = a + b; while(c < k) a = b,b = c,c = a + b; cout << "m=" << a << endl << "n=" << b; }
写在最后：
我叫风骨散人，名字的意思是我多想可以不低头的自由生活，可现实却不是这样。家境贫寒，总得向这个世界低头，所以我一直在奋斗，想改变我的命运给亲人好的生活，希望同样被生活绑架的你可以通过自己的努力改变现状，深知成年人的世界里没有容易二字。目前是一名在校大学生，预计考研，热爱编程，热爱技术，喜欢分享，知识无界，希望我的分享可以帮到你！
如果有什么想看的，可以私信我，如果在能力范围内，我会发布相应的博文！
感谢大家的阅读！????你的点赞、收藏、关注是对我最大的鼓励！
最后
以上就是无语鞋子最近收集整理的关于算法分析与设计入门级--递推算法（这个要是学不会，就别学算法了）的全部内容，更多相关算法分析与设计入门级--递推算法（这个要是学不会内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复