梯度下降与回归算法1. 机器学习的基本模式2. 线性回归3. 梯度下降python实现参考资料

80 阅读 0 评论 53 点赞

我是靠谱客的博主魔幻白猫，最近开发中收集的这篇文章主要介绍梯度下降与回归算法1. 机器学习的基本模式2. 线性回归3. 梯度下降python实现参考资料，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1. 机器学习的基本模式

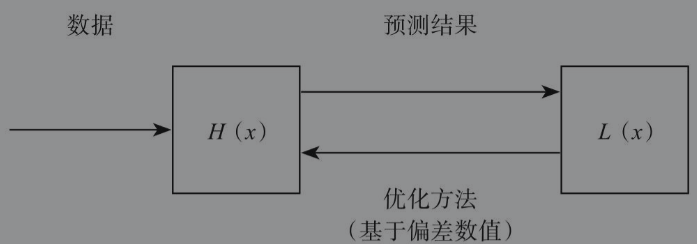
拟合数据（训练模型） --> 进行预测

假设函数（Hypothesis Function）：通常表示为 H(x)，输入数据输出预测值y^。
损失函数（Loss Function）：通常表示为 L(x)，表示预测值与真实值的偏差。。函数返回值越大，表示结果偏差越大。

成本函数（Cost Function）：通常表示为 J(x) ，与损失函数一样表示预测值与真实值的偏差。区别二者的关键在于对象，损失函数是针对单个样本，而成本函数则是针对整个数据集，也就是说，损失函数求得的总和就是成本函数

L2范数和均方误差是机器学习常用的损失函数。
优化方法

优化方法根据损失值调整假设函数的参数以更好地拟合数据。梯度下降（Gradient Descent）法是机器学习中常用的一种优化方法。如果样本数量庞大，完成一次完整的梯度下降需要耗费很长时间，在实际工作中会根据情况调整每次参与损失值计算的样本数量。每次迭代都使用全部样本的，称为批量梯度下降（Batch Gradient Descent）；每次迭代只使用一个样本的，称为随机梯度下降（Stochastic Gradient Descent）。

首先为假设函数设定初始参数，计算得到预测值；其次将预测值带入损失函数，计算损失值；然后通过得到的损失值，利用梯度下降等优化方法，不断调整假设函数的参数w，使得损失值最小，这是一个迭代的过程。

在这里插入图片描述

2. 线性回归

回归问题与分类问题的区别

回归问题和分类问题最大的区别在于预测结果。根据预测值类型的不同，预测结果可以分为两种，一种是连续的，另一种是离散的，结果是连续的就是回归问题。
拟合数据

假设函数：
$h(x)=theta_1^Tx+theta_0$
损失函数：
- 采用L2范数（它的正式名称为“范数正则化”，习惯上简称为“范数”或“正则化”，是指向量各元素的平方和然后求平方根）：
  $L(x)=||hat{y}-y||_2^2$
- 采用均方误差的和，实际上是成本函数：
  $J(Theta)=frac{1}{2m}sum_{i=1}^m(h(x^{(i)})-y^{(i)})^2$
  其中，½是一个常量，这样是为了在求梯度的时候，二次方乘下来就和这里的½抵消了，自然就没有多余的常数系数，方便后续的计算，同时对结果不会有影响。
优化方法：采用梯度下降法
$min_{w,b}J(theta)$

3. 梯度下降

梯度下降（Gradient Descent）法是机器学习中常用的一种优化方法。

梯度是微积分的概念，某个函数在某点的梯度指向该函数取得最大值的方向（给定点上升最快的方向），那么它的反方向自然就是取得最小值的方向（给定点下降最快的方向）。所以我们沿着梯度的反方向走，就能走到局部最小值点。

梯度下降算法：
$theta^{i+1}=theta^i-alphatimes J{'}(theta^i)$
其中，α在梯度下降算法中被称作为学习率或者步长，意味着我们可以通过α来控制每一步走的距离。α不能太大也不能太小，太小的话，可能导致迟迟走不到最低点，太大的话，会导致错过最低点。

python实现

为了将公式矩阵化，我们对每个点x增加一维，这一维固定为1。这一维实际就是参数Θ0。

定义数据集和学习率

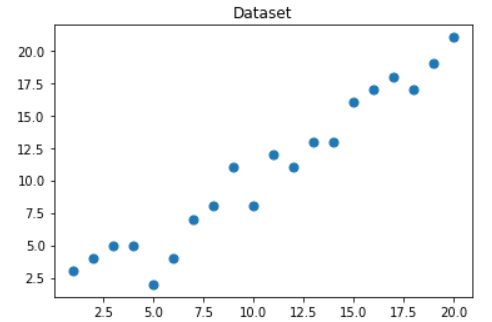
import numpy as np

m = 20	#数据集中点的个数

# X矩阵 --> （x0,x1）
X0 = np.ones((m, 1))
X1 = np.arange(1, m+1).reshape(m, 1)
X = np.hstack((X0, X1))		#水平拼接为m*2的矩阵

# 真实值点y
y = np.array([
    3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
    11, 13, 13, 16, 17, 18, 17, 19, 21
]).reshape(m, 1)

# 学习率
alpha = 0.01

可视化构造的数据样本点

import matplotlib.pyplot as plt
plt.figure()
plt.scatter(x1,y, s=50, cmap='viridis')
plt.title('Dataset')
plt.show()

在这里插入图片描述

以矩阵向量的形式定义代价函数和代价函数的梯度

def error_function(theta, X, y):
    '''代价函数定义'''
    diff = np.dot(X, theta) - y    #np.dot(x,y) <=> x.dot(y) 矩阵乘法
    return (1./(2*m)) * np.dot(np.transpose(diff), diff)    #np.transpose()矩阵转置

def gradient_function(theta, X, y):
    '''代价函数梯度定义'''
    diff = np.dot(X, theta) - y
    return (1./m) * np.dot(np.transpose(X), diff)

梯度下降迭代计算

def gradient_descent(X, y, alpha):
    '''梯度下降'''
    theta = np.array([1, 1]).reshape(2, 1)
    gradient = gradient_function(theta, X, y)
    while not np.all(np.absolute(gradient) <= 1e-5):
        theta = theta - alpha * gradient
        gradient = gradient_function(theta, X, y)
        return theta

运行代码

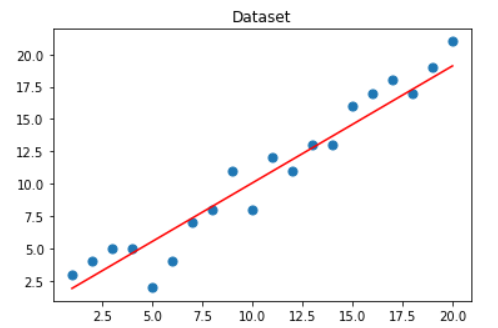
optimal = gradient_descent(X, y, alpha)
print('optimal:', optimal)
print('error function:', error_function(optimal, X, y)[0,0])

optimal: [[0.992]
 [0.906]]
error function: 440.7643999999998

可视化拟合出的直线

import matplotlib.pyplot as plt
plt.figure()
plt.scatter(x1,y, s=50, cmap='viridis')
plt.plot(x1,np.dot(X, optimal), color='red')
plt.title('Dataset')
plt.show()