李宏毅机器学习组队学习打卡活动day04---深度学习介绍和反向传播机制

写在前面

报了一个组队学习的活动，今天的任务是深度学习，深度学习之前没有怎么接触，这次可以好好学习一下。

参考视频:https://www.bilibili.com/video/av59538266
参考笔记：https://github.com/datawhalechina/leeml-notes

深度学习介绍

深度学习的三个步骤

deep learning 一般有三个部分：

• step1:神经网络(Neural network)
• step2: 模型评估(Goodness of function)
• step3: 选择最优函数(Pick best function)
  

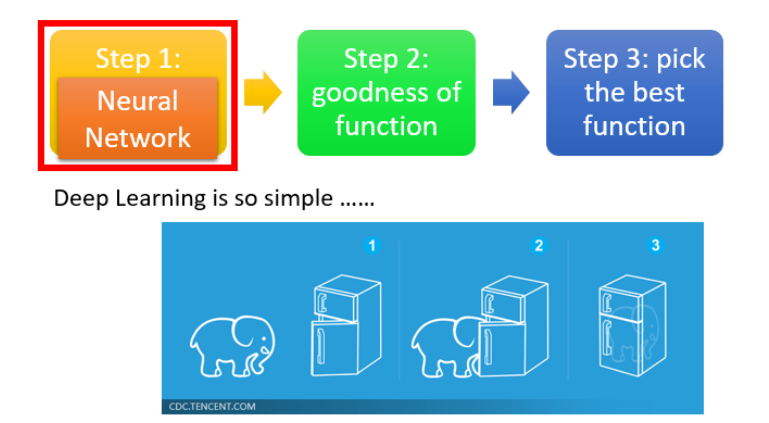
step1:神经网络

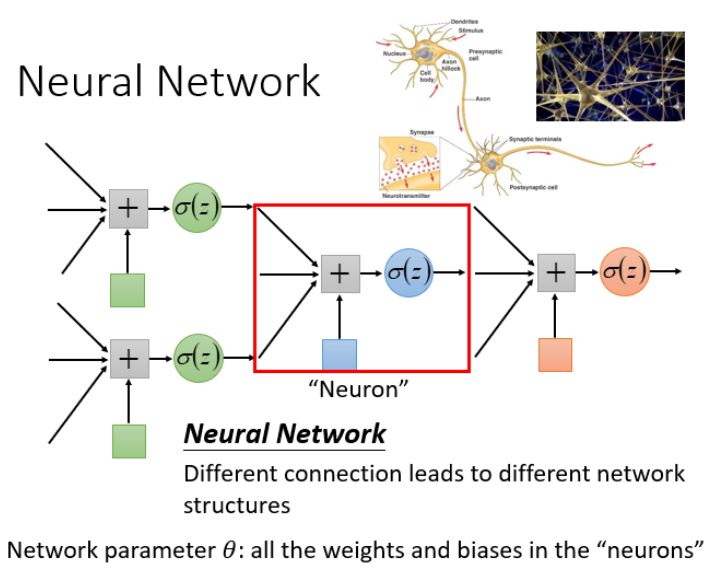
神经元：神经网络里面的节点

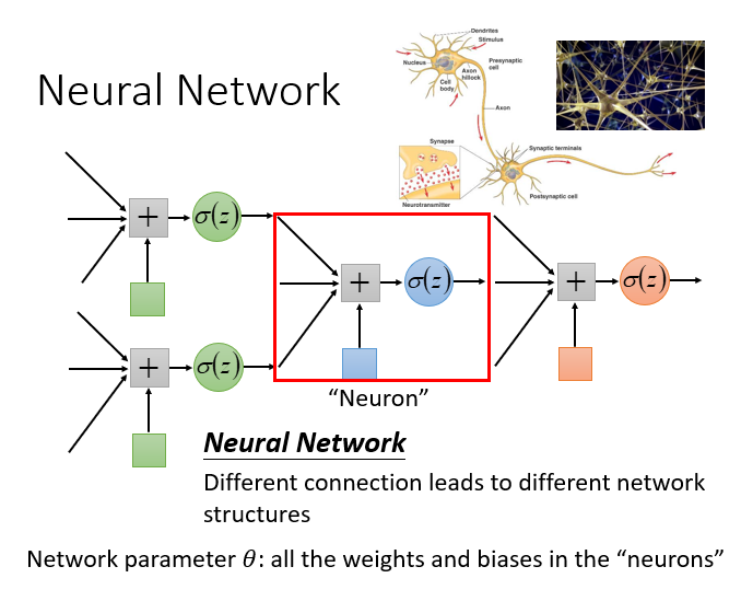
神经网络有很多不同的连接方式，这样会产生不同的结构。

完全前馈神经网络
概念：前馈(feedforward)也可以称为前向，从信号流向来理解就是输入信号进入网络后，信号流动是单项的，即信号从前一层流向后一层，一直到输出层，其中任意两层之间的连接并没有反馈(feedback)，亦即信号没有从后一层又返回到前一层。

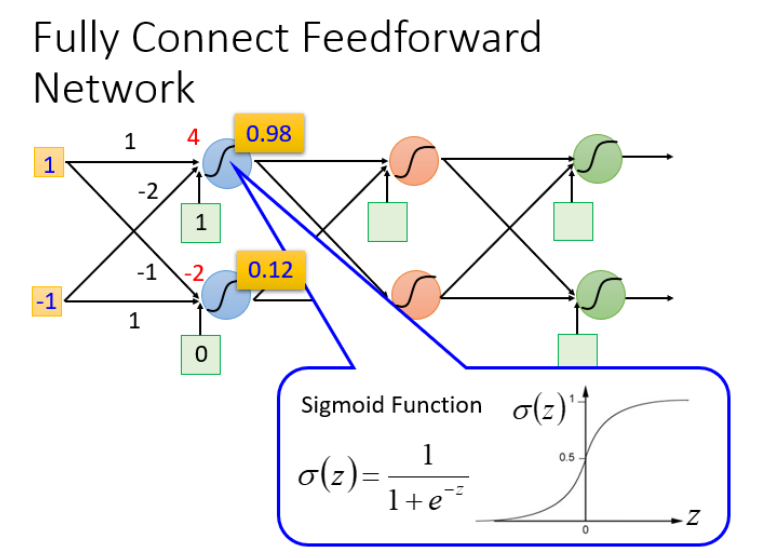
例如输入(1，-1)和(-1,0)的结果：

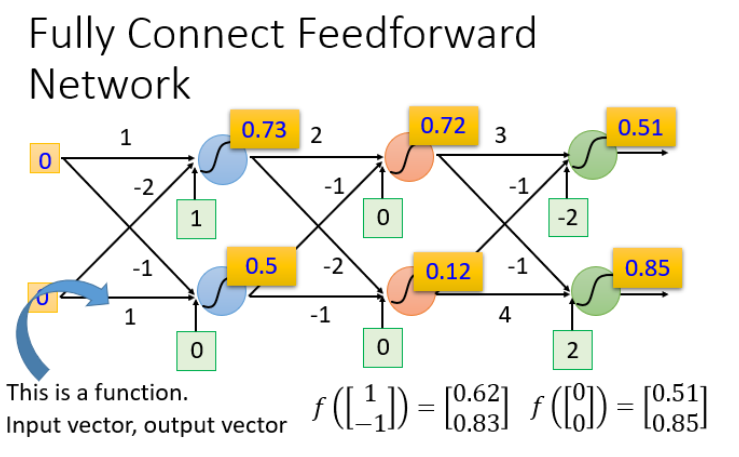
我们可以给上面的结构的参数设置为不同的数，就是不同的函数（function）。这些可能的函数（function）结合起来就是一个函数集（function set）。

全链接和前馈的理解

• 输入层（Input Layer）：1层
• 隐藏层（Hidden Layer）：N层
• 输出层（Output Layer）：1层
  

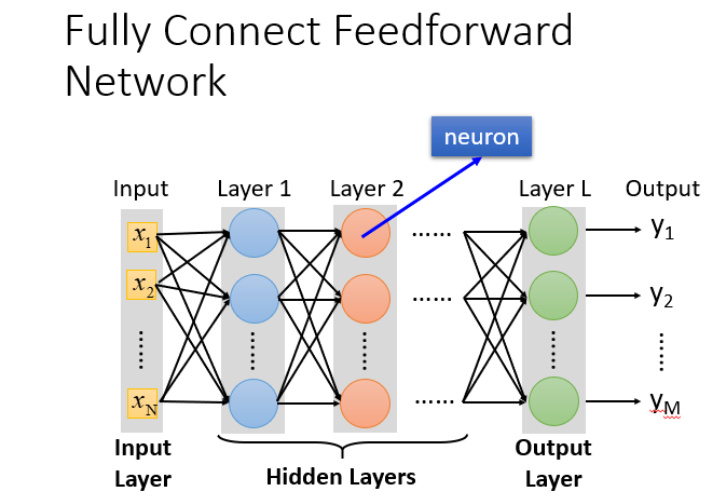
全连接的理解: 因为layer与layer2之间凉凉都有连接，所以叫做全链接(Fully Connect)
前馈的理解: 因为传递的方向是由后往前传，所以叫做Feedforward.

深度的理解
那什么叫做Deep呢？Deep = Many hidden layer。那到底可以有几层呢？
随着层数变多，错误率降低，随之运算量增大，通常都是超过亿万级的计算。采用矩阵运算可以加快运算速度。

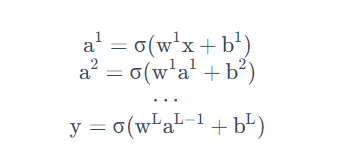
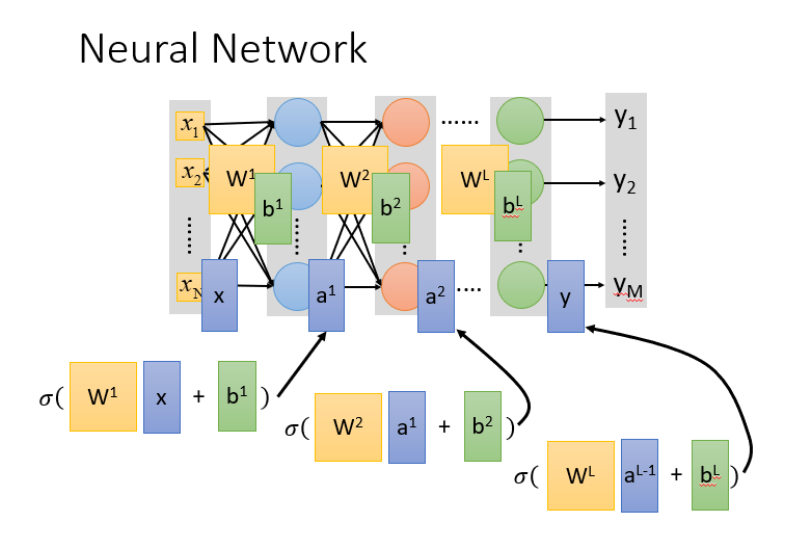
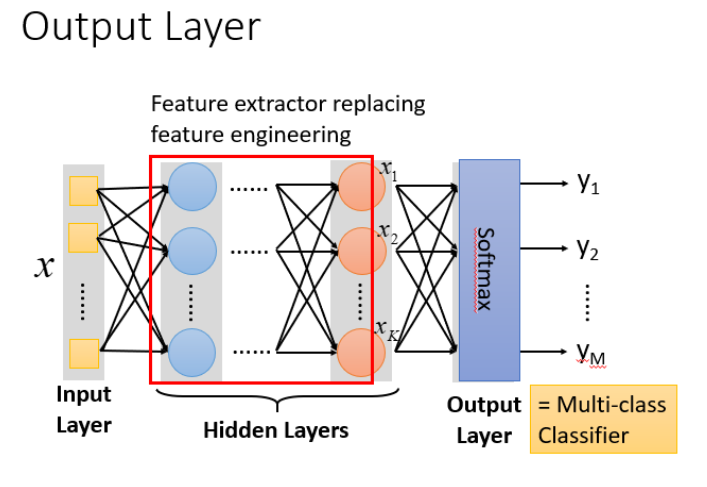
本质：通过隐藏层进行特征转换
把隐藏层通过特征提取来替代原来的特征工程，这样在最后一个隐藏层输出的就是一组新的特征（相当于黑箱操作）而对于输出层，其实是把前面的隐藏层的输出当做输入（经过特征提取得到的一组最好的特征）然后通过一个多分类器（可以是softmax函数）得到最后的输出y。

step2:模型评估

损失示例：

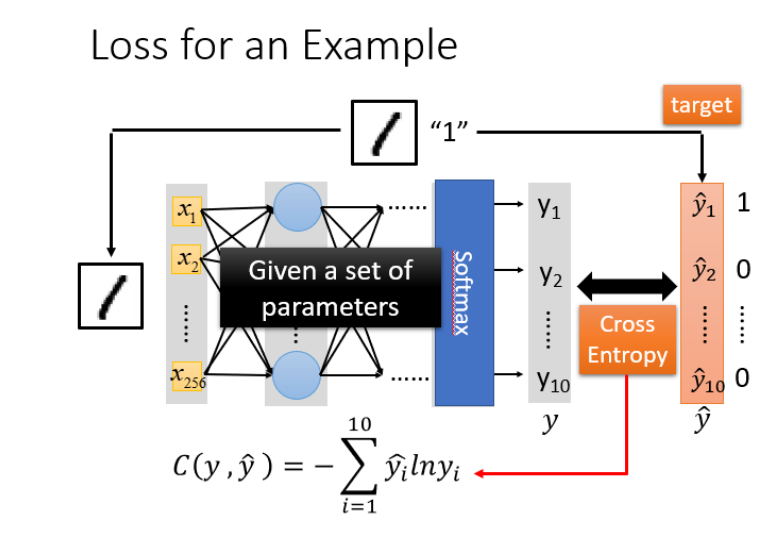
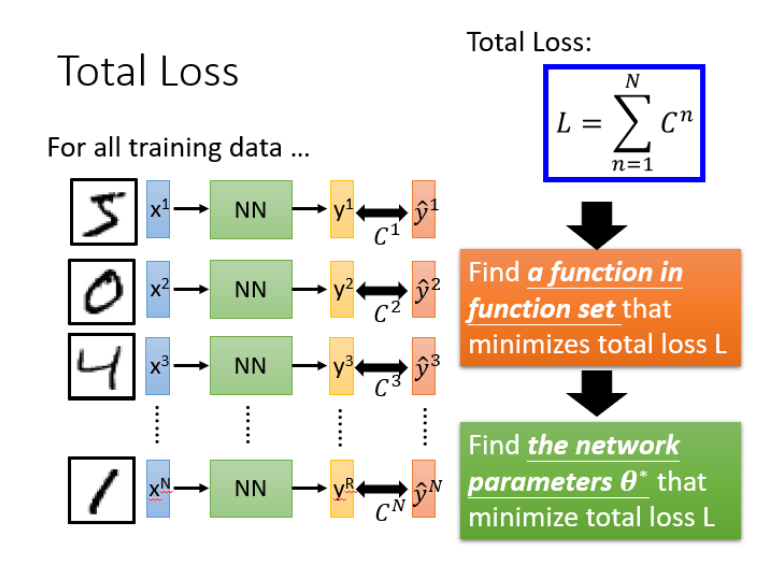
对于损失，我们不单单要计算一笔数据的，而是要计算整体所有训练数据的损失，然后把所有的训练数据的损失都加起来，得到一个总体损失L。
对于模型的评估。我们一般采用损失函数来反映模型的好坏，对于神经网络，一般采用**交叉熵(cross entropy)**函数进行计算。

step3:选择最优函数

梯度下降

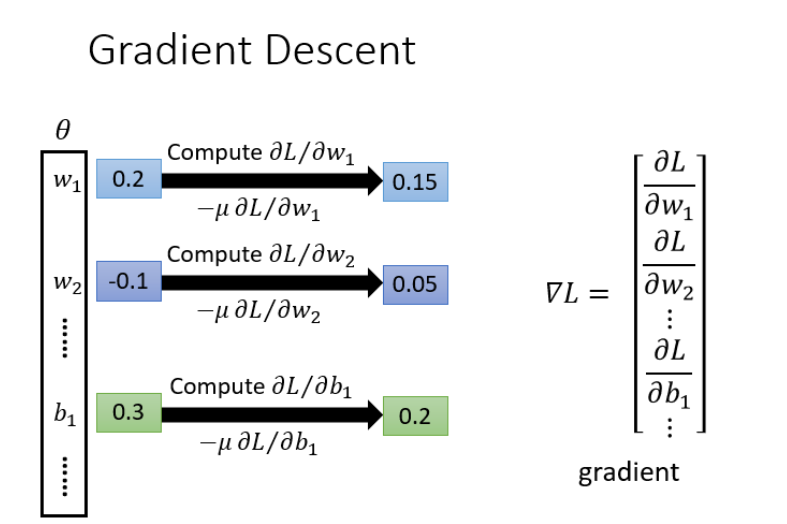
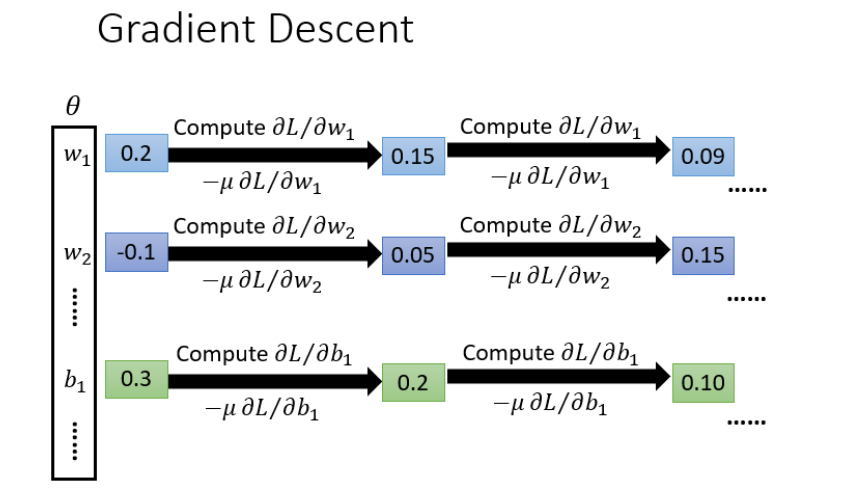
具体流程：$\theta$ 是一组包含权重和偏差的参数集合，随机找一个初试值，接下来计算一下每个参数对应的偏微分，得到一个偏微分的集合$\nabla L$就是梯度，有了这些偏微分，就可以不断更新梯度得到新的参数，这样不断反复进行，就可以得到最好的参数使得损失函数最小。

反向传播

在神经网络钟计算损失最好的方法就是反向传播，可以利用TensorFlow, theano, Pytorch等等框架计算。

1. 损失函数(Loss function) 是定义在单个训练样本上的，也就是算一个样本的误差，
2. 代价函数(Cost function)是定义在整个训练集上的，也就是所有样本的误差的总和的平均。
3. 总体损失函数(Total loss function)是定义在整个训练集上面的，也就是所有样本的误差总和，也就是评估我们反向传播需要最小化的值。
   

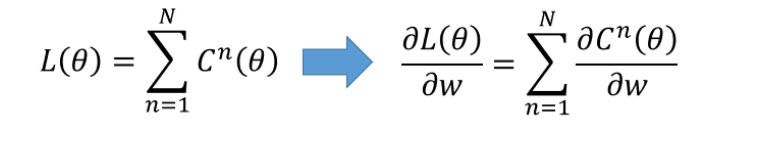
对一个神经元(Neuron)进行分析

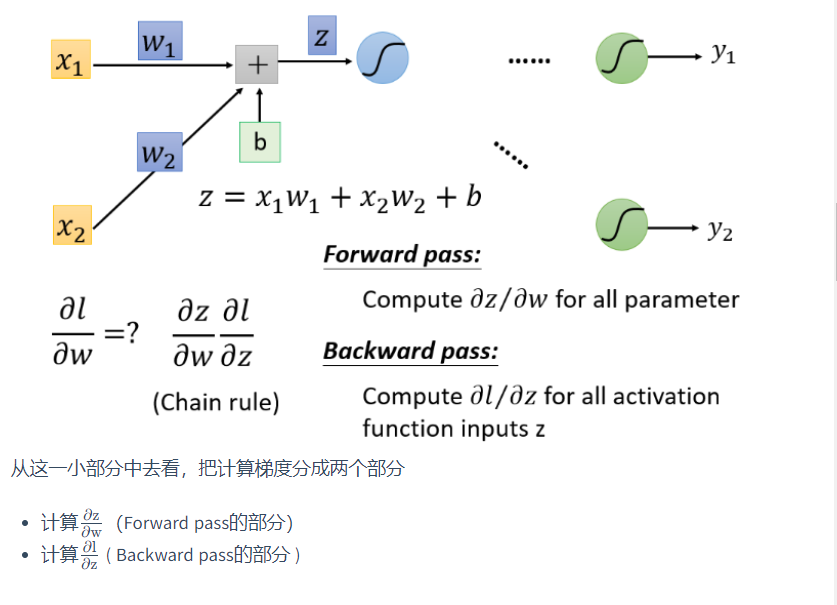
前向部分

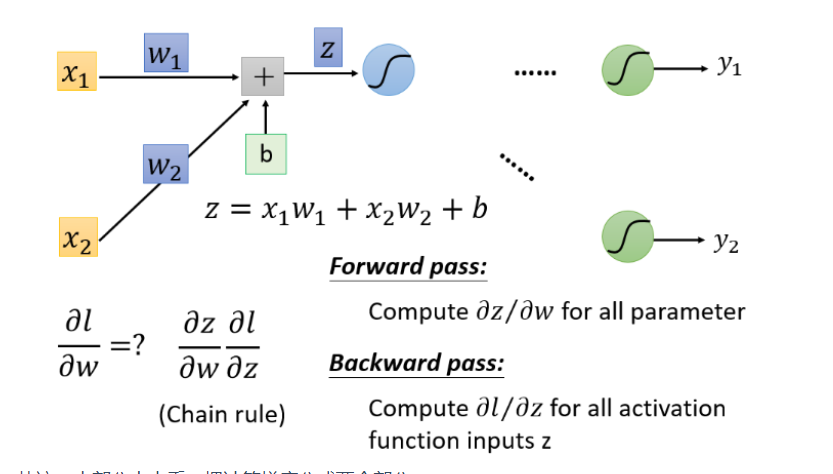
根据微分原理，$\frac{\partial z}{\partial w_1}=x_1$, $\frac{\partial z}{\partial w_2}=x_2$

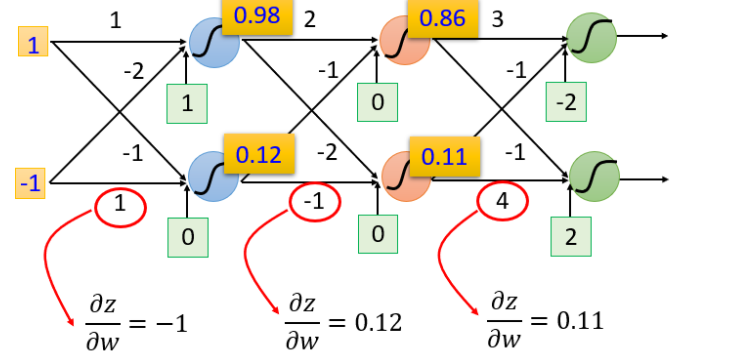
反向部分

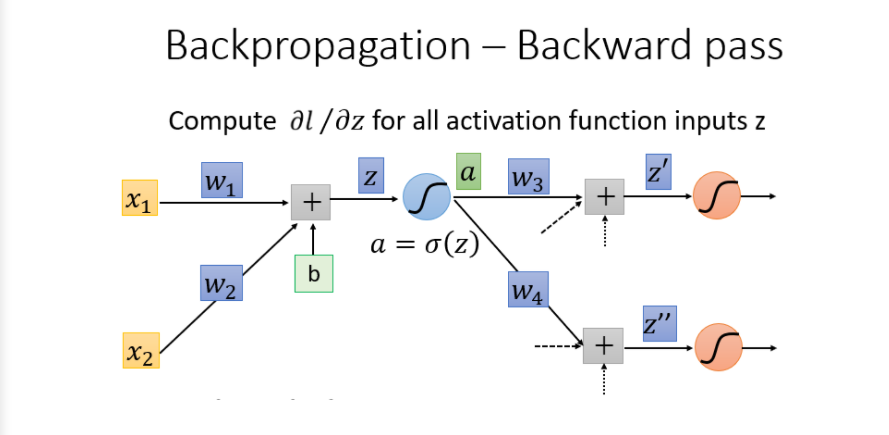
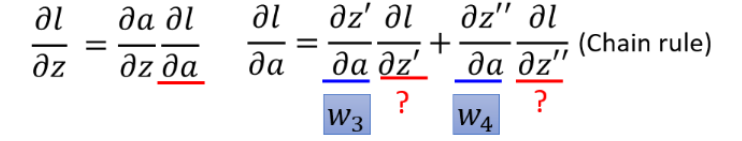
最终结果：

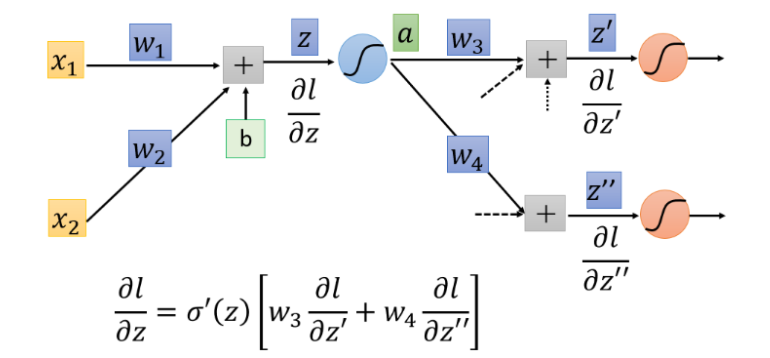
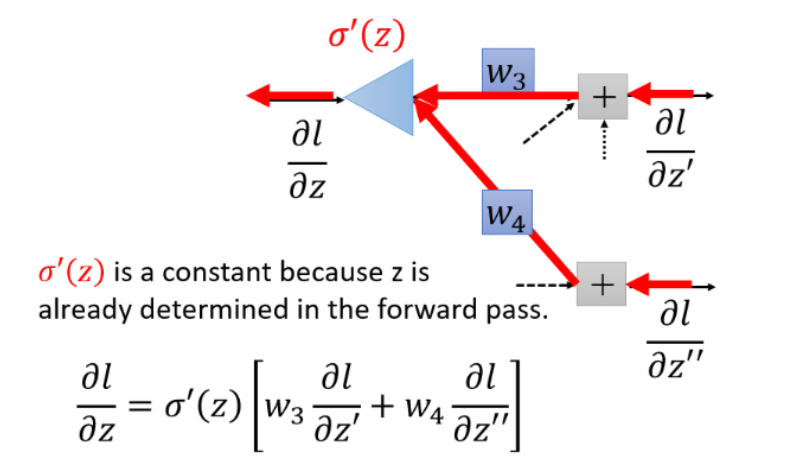
理解：但是你可以想象从另外一个角度看这个事情，现在有另外一个神经元，把forward的过程逆向过来，
其中${\sigma }^{\prime }(z)$是常数，因为它在向前传播的时候就已经确定了。

若$\frac{\partial l}{\partial z^{\prime }}$和$\frac{\partial l}{\partial z^{\prime \prime }}$是最后一层隐藏层，那么直接计算就可以得到结果

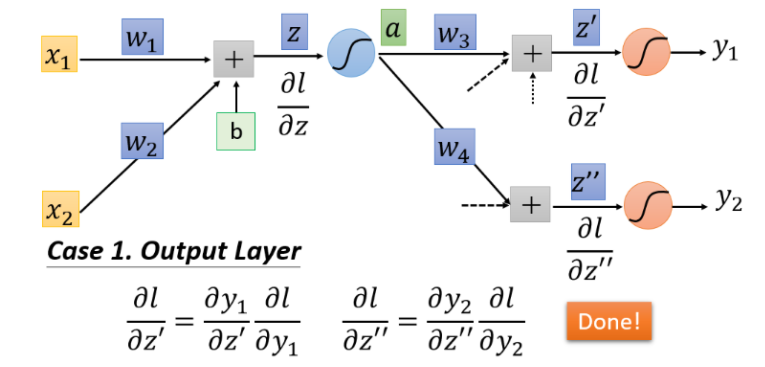
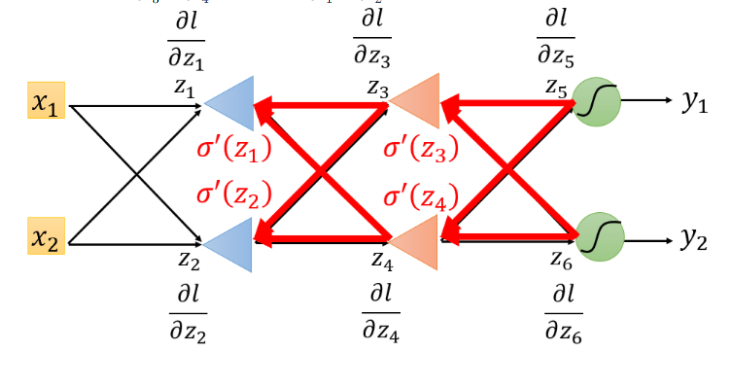
若$\frac{\partial l}{\partial z^{\prime }}$和$\frac{\partial l}{\partial z^{\prime \prime }}$最后一层隐藏层，则需要一直往后通过链式法则计算下去

总结

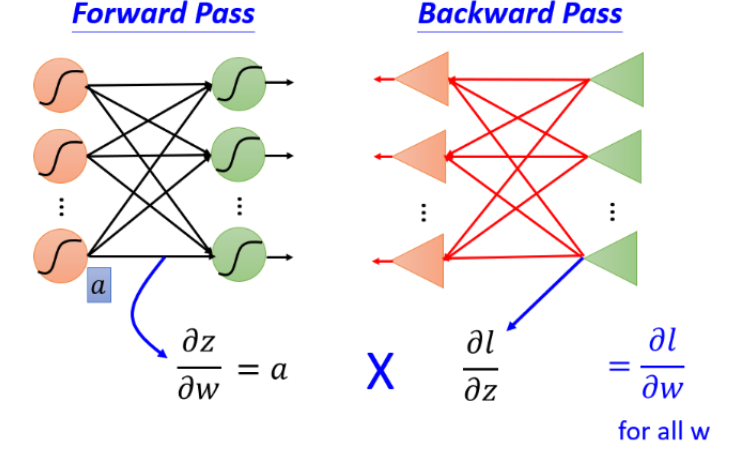
我们的目标就是计算$\frac{\partial z}{\partial w}$(Forward pass部分)和计算KaTeX parse error: Undefined control sequence: patial at position 19: …ac{partial l}{̲p̲a̲t̲i̲a̲l̲ ̲z}(Backward pass的部分)，然后将$\frac{\partial z}{\partial w}$和KaTeX parse error: Undefined control sequence: patial at position 19: …ac{partial l}{̲p̲a̲t̲i̲a̲l̲ ̲z}相乘就可以得到
$\frac{\partial l}{\partial w}$，就可以得到神经网络中所有的参数，然后用梯度下降不断更新，得到损失最小函数。

最后

以上就是冷傲柚子为你收集整理的李宏毅机器学习组队学习打卡活动day04---深度学习介绍和反向传播机制的全部内容，希望文章能够帮你解决李宏毅机器学习组队学习打卡活动day04---深度学习介绍和反向传播机制所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。